O deuteron
Notas de aula são propriedade intelectual. Sendo assim, qualquer uso, no todo ou em parte, deve ter a origem referenciada apropriadamente, após autorização de seu autor.
O texto a seguir corresponde à anotações parciais de aula. Não é um texto em forma final, completo e totalmente revisado. Nesse caso, esse texto não tem como objetivo substituir livros sobre o assunto. Assim, esse texto deve ser entendido apenas como um guia de estudo para o aluno acompanhar a disciplina.
Vamos estudar em detalhes o dêuteron. A partir da construção de um modelo simples para a interação entre próton e nêutron, comparando os resultados desse modelo com medidas experimentais de elevada precisão, tentaremos inferir propriedades sobre as forças nucleares fortes que tornam o núcleo estável.
Vamos inicialmente listar algumas informações experimentais sobre o dêuteron. Como elas são determinadas em detalhes não vêm ao caso nesse momento:
- Energia de ligação do dêuteron: medidas indicam que só há um estado ligado do dêuteron com energia de ligação
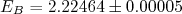 MeV. Alguns métodos de medidas foram discutidos anteriormente.
MeV. Alguns métodos de medidas foram discutidos anteriormente.
- Raio o dêuteron: medidas de espalhamento de elétrons indicam que o raio do dêuteron é aproximadamente 2.1 fm.
- Momento angular e paridade: medidas através de métodos ópticos e micro-ondas indicam que o momento angular total do dêuteron é
 . Através de medidas de desintegrações nucleares, através da conservação da paridade e comparação com modelos teóricos, mostram que o dêuteron deve possuir função de onda par.
. Através de medidas de desintegrações nucleares, através da conservação da paridade e comparação com modelos teóricos, mostram que o dêuteron deve possuir função de onda par.
- Momento de quadrupolo elétrico: Medidas realizadas na década de 1930 mostraram que o dêuteron é um núcleo prolato ao longo do seu eixo de spin, com momento de quadrupolo elétrico
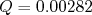 barns.
barns.
- Momento de dipolo magnético: O momento de dipolo magnético do dêuteron pode ser obtido através de métodos de ressonância magnética, na qual pode-se ajustar um campo magnético oscilante de frequência igual à frequência de Lamour para o dêuteron. A frequência de Lamour está relacionada diretamente ao momento de dipolo magnético que, nesse caso, vale
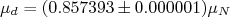 , onde
, onde 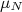 é o magneton nuclear.
é o magneton nuclear.
Primeiramente vamos olhar o momento de dipolo magnético. A soma do momento de dipolo do próton e nêutron vale
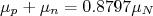 , muito próximo ao valor para o dêuteron. Essa soma simples sugere que os spins do próton e nêutron devam, em primeira aproximação, estar alinhados e que o momento angular orbital entre eles seja muito pequeno,
, muito próximo ao valor para o dêuteron. Essa soma simples sugere que os spins do próton e nêutron devam, em primeira aproximação, estar alinhados e que o momento angular orbital entre eles seja muito pequeno,  . Contudo, a elevada precisão das medidas experimentais tornam essa soma incompatível com o valor medido. Vamos retomar isso mais a frente. Contudo, vamos usar que essa relação é aproximadamente satisfeita como ponto de partida.
. Contudo, a elevada precisão das medidas experimentais tornam essa soma incompatível com o valor medido. Vamos retomar isso mais a frente. Contudo, vamos usar que essa relação é aproximadamente satisfeita como ponto de partida.
Vamos resolver a Equação de Schrödinger no centro de massa do sistema próton-nêutron. Sendo
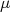 a massa reduzida desse sistema, temos:
a massa reduzida desse sistema, temos:
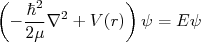 (1)
(1)Supondo que o potencial é central, podemos escrever a função de onda como sendo o produto de uma função radial por uma função que depende dos ângulos polar e azimutal, ou seja:
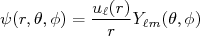 (2)
(2)Nessa separação de variáveis, conserva-se o momento angular orbital relativo entre as partículas. A parte angular possui solução trivial (harmônicos esféricos) enquanto a parte radial contém toda informação acerca do potencial. Nesse caso, para entender a interação entre as partículas, precisamos resolver a equação radial:
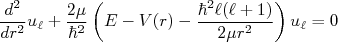 (3)
(3)O potencial mais simples que podemos utilizar para o dêuteron é um poço quadrado radial, ou seja:
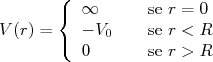 (4)
(4)O fato dele do potencial ser infinito a curtas distâncias representa a saturação da densidade nuclear, como visto no início da disciplina. A proximidade do momento de dipolo magnético do dêuteron com a soma dos momentos do próton e nêutron, como vimos, sugere que o momento angular relativo seja nulo. Assim, fazendo
 em (3) temos a seguinte equação:
em (3) temos a seguinte equação:
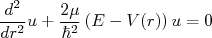 (5)
(5)Vamos resolver esse sistema para o estado fundamental do dêuteron, ou seja,
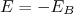 . Definindo
. Definindo 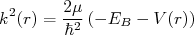 , podemos escrever a equação (5) como:
, podemos escrever a equação (5) como:
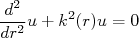 (6)
(6)A equação (6) pode ser separada em duas, dependendo da região do potencial: ou seja, para
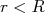 (região I):
(região I):
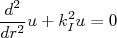 (7)
(7)e, para
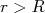 (região II):
(região II):
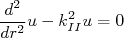 (8)
(8)com
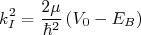 e
e 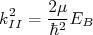 . As soluções de (7) e (8), considerando que
. As soluções de (7) e (8), considerando que 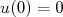 são, respectivamente:
são, respectivamente:
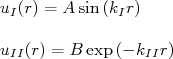 (9)
(9)Aplicando as condições de contorno em
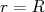 para a continuidade da função de onda e sua derivada, temos:
para a continuidade da função de onda e sua derivada, temos:
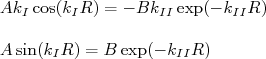 (10)
(10)Dividindo as duas equações temos:
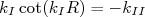 (11)
(11)Resolvendo numericamente ou graficamente (11), usando os dados experimentais para
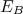 e
e 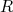 , obtemos que o valor da profundidade do poço de potencial é
, obtemos que o valor da profundidade do poço de potencial é  MeV. Pode-se mostrar (exercício) que não existe outro estado ligado para o dêuteron com momento angular nulo. Nesse caso, pode-se inferir que em outros momentos angulares a situação torna-se pior por conta do potencial centrífugo que surge quando o momento angular não é nulo.
MeV. Pode-se mostrar (exercício) que não existe outro estado ligado para o dêuteron com momento angular nulo. Nesse caso, pode-se inferir que em outros momentos angulares a situação torna-se pior por conta do potencial centrífugo que surge quando o momento angular não é nulo.
Nós já vimos, contudo, que o estado
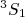 sozinho (ver início das notas) não consegue explicar o momento de dipolo magnético do dêuteron, apesar de fornecer um valor próximo. Pode-se argumentar que
sozinho (ver início das notas) não consegue explicar o momento de dipolo magnético do dêuteron, apesar de fornecer um valor próximo. Pode-se argumentar que 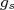 seja diferente para o estado ligado desses nucleons mas esse estado também não consegue explicar o modelo de quadrupolo elétrico experimental do dêuteron. Assim, vamos tentar construir uma função de onda para o dêuteron através de uma mistura de estados de momento angular, impondo a restrição que o momento angular total observado para esse estado ligado é
seja diferente para o estado ligado desses nucleons mas esse estado também não consegue explicar o modelo de quadrupolo elétrico experimental do dêuteron. Assim, vamos tentar construir uma função de onda para o dêuteron através de uma mistura de estados de momento angular, impondo a restrição que o momento angular total observado para esse estado ligado é  . As possíveis combinações de momento angular e spin para
. As possíveis combinações de momento angular e spin para  são:
são:
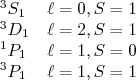 (12)
(12)Pelo fato do dêuteron possuir paridade definida, podemos misturar apenas estados de mesma paridade. Assim, as possíveis combinações são
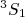 e
e 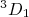 (estados pares) ou
(estados pares) ou 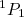 e
e 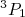 (paridade ímpar). Sabemos que o estado S pode explicar grande parte do momento de dipolo magnético. Assim, vamos explorar apenas a primeira combinação possível.
(paridade ímpar). Sabemos que o estado S pode explicar grande parte do momento de dipolo magnético. Assim, vamos explorar apenas a primeira combinação possível.
O problema consiste em achar a função de onda para essa combinação de estados. Nós sabemos as funções de onda para estados bem definidos
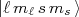 , que são harmônicos esféricos ou matrizes de Pauli para estados de spin 1/2. Contudo, sabemos que o estado do dêuteron é definido pela função de onda
, que são harmônicos esféricos ou matrizes de Pauli para estados de spin 1/2. Contudo, sabemos que o estado do dêuteron é definido pela função de onda 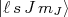 . Assim, devemos escrever essa última como combinação de estados das outras. Além disso devemos considerar que o estado de spin do dêuteron consiste na soma do spin de dois nucleons. Para a combinação de estado S e D, temos que o spin total é sempre 1. Nesse caso, antes de encontrar a função de onda total com
. Assim, devemos escrever essa última como combinação de estados das outras. Além disso devemos considerar que o estado de spin do dêuteron consiste na soma do spin de dois nucleons. Para a combinação de estado S e D, temos que o spin total é sempre 1. Nesse caso, antes de encontrar a função de onda total com  vamos encontrar apenas a parte de spin. Nesse caso, queremos encontrar o estado de spin
vamos encontrar apenas a parte de spin. Nesse caso, queremos encontrar o estado de spin 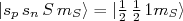 . Para
. Para  , podemos ter três funções de onda distintas que correspondem a
, podemos ter três funções de onda distintas que correspondem a  . Em linhas gerais, usando o formalismo de somas de momento angular, podemos escrever que um estado de soma de spins é a soma de todos os estados possíveis de spins individuais, ponderados pelos coeficientes de Clebsh-Gordam correspondentes, ou seja:
. Em linhas gerais, usando o formalismo de somas de momento angular, podemos escrever que um estado de soma de spins é a soma de todos os estados possíveis de spins individuais, ponderados pelos coeficientes de Clebsh-Gordam correspondentes, ou seja:
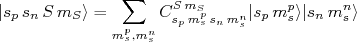 (13)
(13)Para o estado
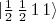 só há uma combinação de soma possível, nesse caso:
só há uma combinação de soma possível, nesse caso:
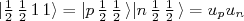 (14)
(14)Similarmente para o estado
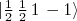 :
:
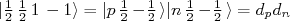 (15)
(15)No qual definimos uma notação mais simples
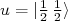 e
e 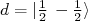 , em analogia ao spin up e spin down. No caso do estado
, em analogia ao spin up e spin down. No caso do estado 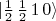 , há duas possibilidades de combinação de spins. Nesse caso, consultanto tabelas de coeficientes de acoplamento de momento angular, podemos escrever que:
, há duas possibilidades de combinação de spins. Nesse caso, consultanto tabelas de coeficientes de acoplamento de momento angular, podemos escrever que:
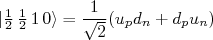 (16)
(16)As equações (14), (15) e (16) representam as três combinações possíveis de estados tripletos de spin (
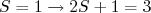 ). O momento angular total pode ser obtido, para os estados
). O momento angular total pode ser obtido, para os estados 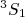 e
e 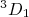 , acoplando os estados de momento angular orbital com as funções de onda de spin total.
, acoplando os estados de momento angular orbital com as funções de onda de spin total.
Para o estado
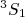 a situação é bem simples. Como o momento de dipolo magnético é calculado na situação
a situação é bem simples. Como o momento de dipolo magnético é calculado na situação  , e como a onda com
, e como a onda com  não é degenerada, há apenas uma combinação possível. Assim:
não é degenerada, há apenas uma combinação possível. Assim:
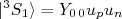 (17)
(17)Para o estado
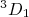 , os únicos termos que contribuem para
, os únicos termos que contribuem para 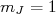 compõem o seguinte estado:
compõem o seguinte estado:
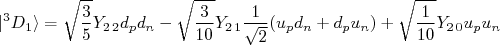 (18)
(18)Como visto anteriormente, o operador de momento de dipolo magnético pode ser escrito como um termo orbital, que atua somente sobre o próton e um termo de spin, atuando sobre próton e nêutron. Assim,
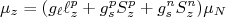 (19)
(19)Como o momento angular do próton é metade do momento angular relativo no centro de massa, temos:
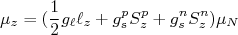 (20)
(20)A contribuição de momento de dipolo para o estado
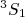 vale:
vale:
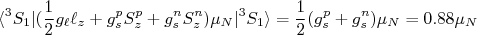 (21)
(21)O mesmo pode ser feito para o estado
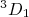 , obtendo-se o resultado
, obtendo-se o resultado 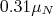 (exercício). O momento de dipolo magnético experimental do dêuteron é
(exercício). O momento de dipolo magnético experimental do dêuteron é 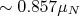 , intermediário entre os valores desses dois estados pares. Assim, podemos admitir que a função de onda do dêuteron é uma combinação desses dois estados, ou seja:
, intermediário entre os valores desses dois estados pares. Assim, podemos admitir que a função de onda do dêuteron é uma combinação desses dois estados, ou seja:
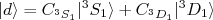 (22)
(22)onde:
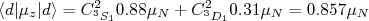 (23)
(23)Considerando que a função de onda do dêuteron deve ser normalizada, ou seja
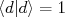 , chega-se ao resultado
, chega-se ao resultado 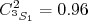 e
e  .
.
Resultado similar pode ser obtido considerando o momento de quadrupolo elétrico (exercício). Contudo, o importante desse trabalho é concluir que o dêuteron é formado da combinação de dois estados de momento angular orbital diferentes, apesar da contribuição de
 ser bastante pequena. Isso terá consequências importantes no entendimento das forças nucleares. O dêuteron não é um estado de momento angular orbital único. Assim, momento angular orbital não é uma constante de movimento. Veremos o efeito disso a seguir.
ser bastante pequena. Isso terá consequências importantes no entendimento das forças nucleares. O dêuteron não é um estado de momento angular orbital único. Assim, momento angular orbital não é uma constante de movimento. Veremos o efeito disso a seguir.
Exercícios
- Mostre que, no caso do dêuteron, considerando o potencial de interação com profundidade de 34 MeV e raio igual ao raio do dêuteron, há somente um estado ligado.
- Mostre que uma combinação de estados
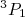 e
e 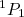 não é capaz de explicar o momento de dipolo magnético do dêuteron.
não é capaz de explicar o momento de dipolo magnético do dêuteron.
- Mostre que
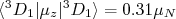 . Dica: Obtenha a função de onda de spin para o estado
. Dica: Obtenha a função de onda de spin para o estado 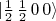 . Esse estado aparece quando se calcula esse valor esperado.
. Esse estado aparece quando se calcula esse valor esperado.
- Obtenha a fração de mistura de estados
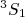 e
e 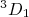 a partir do cálculo de momento de quadrupolo elétrico. Compare com o resultado obtido nessa aula.
a partir do cálculo de momento de quadrupolo elétrico. Compare com o resultado obtido nessa aula.
Leitura recomendada
- Introductory Nuclear Physics, K. S. Krane, capítulo 4.1.
- Introdução à Física Nuclear, H. Schechter e C. A. Bertulani, capítulos 2.1-2.4.
three comments
Oi Suaide, estou com uma dúvida: a equação (9) da função de onda do deuteron no poço finito é um seno, devido à escolha da condição de contorno u(0)=0 na equação (7). Entretanto, o seno é uma função ímpar, e a paridade do neutron é positiva. Como a parte de spin é simétrica (up,up) e o momento angular é zero, a função espacial não deveria ser um cosseno (que é par)? Acho que isso não mudaria a profundidade do poço na solução da equação (11), mas a forma da função de onda seria bastante diferente, pois em r=0 haveria um máximo, não um mínimo!

Olá Caio
Corrigi as equações. Foi uma distração em uma delas e uma sequência de copy/paste que propagou o erro.
Sobre o seu segundo comentário, a questão da função ímpar. Lembre-se que o seno é só o termo radial e não a função de onda completa. Veja a equação (12) na aula sobre paridade em http://sampa.if.usp.br/~suaide/blog/?e=1..
O operador paridade troca o vetor r por menos r. VETOR! Isso resulta na manutenção do módulo ®, e a parte radial não muda o sinal. Nesse caso a paridade vem da parte angular. Como o momento angular orbital é par (l=0) a função de onda é par.




Uma pequena correção: nas equações (14), (15), (16), (17) e (18), acho que o estado de spin up e down do neutron deveria ser escrito u_{n}, ao invés de u_{d} (índice “n” no lugar do índice “d”, que pode confundir com o próprio deuteron).