Paridade, momento angular e isospin
Notas de aula são propriedade intelectual. Sendo assim, qualquer uso, no todo ou em parte, deve ter a origem referenciada apropriadamente, após autorização de seu autor.
O texto a seguir corresponde à anotações parciais de aula. Não é um texto em forma final, completo e totalmente revisado. Nesse caso, esse texto não tem como objetivo substituir livros sobre o assunto. Assim, esse texto deve ser entendido apenas como um guia de estudo para o aluno acompanhar a disciplina.
Nessa aula vamos descrever três propriedades importantes do núcleo atômico, que servem para estabelecer características intrínsecas do seu estado quântico. Em sistemas nucleares, com exceções bem estabelecidas, a conservação dessas grandezas estabelece a ocorrência de determinados tipos de reações ou decaimentos radioativos. São elas:
- Paridade
- Momento angular e spin
- Isospin
Constantes de movimento em M.Q.
Vamos relembrar inicialmente alguns conceitos relacionados a invariâncias e leis de conservação em mecância quântica. Uma grandeza física qualquer pode ser obtida através do valor esperado do seu operador em relação ao estado quântico estudado, ou seja: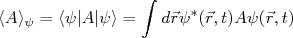 (1)
(1)Se a grandeza é uma constante do movimento, a sua variação no tempo é nula, ou seja:
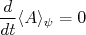 (2)
(2)Expandindo (2) a partir de (1), temos:
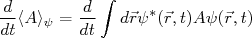
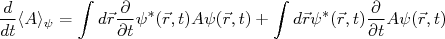
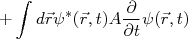 (3)
(3)A partir da equação de Schrödinger dependente do tempo:
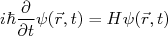 (4)
(4)Podemos reescrever (3) como:
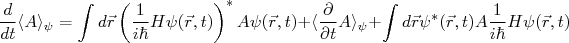 (5)
(5)Sabendo que
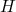 é hermitiano, podemos rescrever a primeira integral e, reorganizando as integrais acima, temos:
é hermitiano, podemos rescrever a primeira integral e, reorganizando as integrais acima, temos:
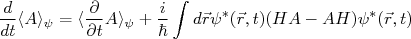
![\frac{d}{dt} \langle A \rangle_{\psi} = \langle \frac{\partial}{\partial t}A \rangle_{\psi} + \frac{i}{\hbar} \langle [H,A] \rangle_{\psi} \frac{d}{dt} \langle A \rangle_{\psi} = \langle \frac{\partial}{\partial t}A \rangle_{\psi} + \frac{i}{\hbar} \langle [H,A] \rangle_{\psi}](/~suaide/blog/pivotx/extensions/renderlatex/pictures/d07173f8c71a99ea454ff2baabfaa76f.png) (6)
(6)A equação (6), mostra que, caso o operador
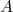 não dependa explicitamente do tempo e caso
não dependa explicitamente do tempo e caso ![[H,A]=0 [H,A]=0](/~suaide/blog/pivotx/extensions/renderlatex/pictures/0026e974fefdeb2487d5d0bc2b9e10f4.png) , então o valor médio de
, então o valor médio de 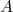 é constante. Nesse caso, podemos dizer que essa grandeza é uma constante do movimento. Essa igualdade é particularmente importante pois permite obter claramente quais são as constantes de movimento de um sistema quântico.
é constante. Nesse caso, podemos dizer que essa grandeza é uma constante do movimento. Essa igualdade é particularmente importante pois permite obter claramente quais são as constantes de movimento de um sistema quântico.
Um aspecto interessante da equação (6) é a consequência que, se houver estados quânticos que sejam, simultaneamente, auto-estados de um operador
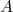 e da Hamiltoniana do sistema, a grandeza
e da Hamiltoniana do sistema, a grandeza 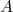 será uma constante do movimento. Para mostrar isso, basta aplicar o comutador desse operador e da Hamiltoniana nesses auto-estados, supondo
será uma constante do movimento. Para mostrar isso, basta aplicar o comutador desse operador e da Hamiltoniana nesses auto-estados, supondo 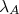 e
e 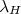 auto-valores de
auto-valores de 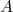 e
e 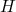 , respectivamente:
, respectivamente:
![[H,A]|\psi\rangle = (HA - AH)|\psi\rangle = HA|\psi\rangle - AH|\psi\rangle = H\lambda_A|\psi\rangle - A\lambda_H|\psi\rangle [H,A]|\psi\rangle = (HA - AH)|\psi\rangle = HA|\psi\rangle - AH|\psi\rangle = H\lambda_A|\psi\rangle - A\lambda_H|\psi\rangle](/~suaide/blog/pivotx/extensions/renderlatex/pictures/1668c97f4ed72becd3df09eb664d770e.png)
![[H,A]|\psi\rangle = \lambda_AH|\psi\rangle - \lambda_HA|\psi\rangle = \lambda_A\lambda_H|\psi\rangle - \lambda_H\lambda_A|\psi\rangle = 0 [H,A]|\psi\rangle = \lambda_AH|\psi\rangle - \lambda_HA|\psi\rangle = \lambda_A\lambda_H|\psi\rangle - \lambda_H\lambda_A|\psi\rangle = 0](/~suaide/blog/pivotx/extensions/renderlatex/pictures/67aaf11cf1f36806f54407135823638f.png)
![[H,A]|\psi\rangle = 0 \rightarrow [H,A] = 0 [H,A]|\psi\rangle = 0 \rightarrow [H,A] = 0](/~suaide/blog/pivotx/extensions/renderlatex/pictures/39e5ef564af2d9f8ee8e44c60c8a0a3a.png) (7)
(7)Paridade
Com base nos argumentos acima, vamos estudar algumas propriedades de sistemas nucleares. Iniciaremos com a Paridade. O operador paridade pode ser definido como o operador que espelha as coordenadas de um sistema quântico, ou seja: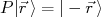 (8)
(8)Aplicando novamente o operador paridade em (8), temos:
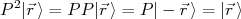 (9)
(9)Ou seja, o operador
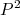 é unitário. Isso sugere que os auto-estados do operador paridade possuam auto-valores
é unitário. Isso sugere que os auto-estados do operador paridade possuam auto-valores 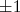 , ou seja:
, ou seja:
 (10)
(10)As únicas funções cujo espelhamento das coordenadas espaciais retornam a mesma função, mudando (ou não) apenas os seus sinais são as chamadas funções pares e ímpares. Em uma função par
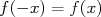 enquanto em uma função ímpar,
enquanto em uma função ímpar,  .
.
Uma consequência óbvia é que a qualquer auto-estado que seja uma função par ou ímpar por reflexão das suas coordenadas também será um auto-estado da paridade. Assim, caso os auto-estados de uma Hamiltoniana sejam funções pares ou ímpares, a paridade será uma constante do sistema. Para que os auto-estados de uma Hamiltoniana possuam paridade bem definidas é necessário que o potencial de interação seja uma função par. Isso pode ser demonstrado calculando-se explicitamente o comutador
![[H,P] [H,P]](/~suaide/blog/pivotx/extensions/renderlatex/pictures/47a3bfc5c81da0c806ef51bc677e9639.png) . Esse será nulo se o potencial de interação for par. Essa afirmação tem implicações importantes em física nuclear pois, caso seja uma grandeza conservada, a paridade acaba impondo regras de seleção importantes em reações e decaimentos nucleares.
. Esse será nulo se o potencial de interação for par. Essa afirmação tem implicações importantes em física nuclear pois, caso seja uma grandeza conservada, a paridade acaba impondo regras de seleção importantes em reações e decaimentos nucleares.
Em um sistema cujo potencial é radial, pode-se escrever a função de onda como sendo:
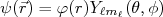 (11)
(11)Aplicando o operador paridade nessa função de onda, temos:
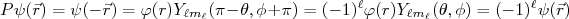 (12)
(12)Isto é, a paridade de uma função de onda obtida de um potencial central é definida pelo momento angular e será par se
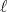 for par e ímpar, se
for par e ímpar, se 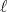 for ímpar. Em um sistema de múltiplas partículas, o estado final desse sistema pode ser escrito como o produto dos estados individuais de cada uma das partículas. Se todas as partículas possuírem paridade bem definida, a paridade do sistema final será o produto das paridades individuais.
for ímpar. Em um sistema de múltiplas partículas, o estado final desse sistema pode ser escrito como o produto dos estados individuais de cada uma das partículas. Se todas as partículas possuírem paridade bem definida, a paridade do sistema final será o produto das paridades individuais.
Nós já discutimos os critérios necessários para que a paridade seja uma grandeza conservada. O potencial de interação deve ser uma função par. Nesse caso, todos os auto-estados da Hamiltoniana serão pares ou ímpares. Como consequência,
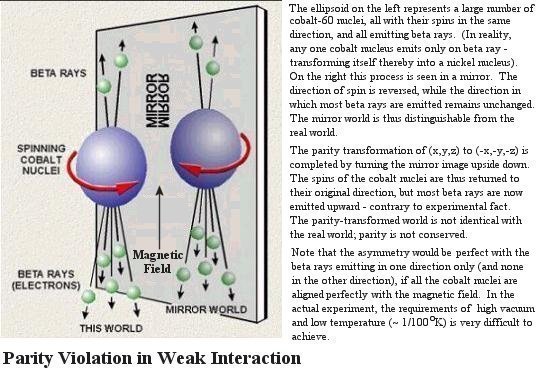
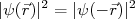 . Se não for o caso, o sistema não conserva a paridade. Em física nuclear em, situações normais, ainda não há evidências de violação de paridade em interações fortes, o que fornece informações importantes sobre a natureza do potencial de interação. Contudo, como veremos mais a frente, decaimentos nuclear β, mediados por interações fracas, não conservam paridade. A violação de paridade em decaimentos β mudou de forma dramática o entendimento acerca das interações fundamentais da Natureza.
. Se não for o caso, o sistema não conserva a paridade. Em física nuclear em, situações normais, ainda não há evidências de violação de paridade em interações fortes, o que fornece informações importantes sobre a natureza do potencial de interação. Contudo, como veremos mais a frente, decaimentos nuclear β, mediados por interações fracas, não conservam paridade. A violação de paridade em decaimentos β mudou de forma dramática o entendimento acerca das interações fundamentais da Natureza.
Momento angular e spin
Quando o potencial de interação é radial, ou seja, apenas uma função da distância entre as partículas que estão interagindo, a determinação dos auto-estados da Hamiltoniana do sistema pode ser feita assumindo que o auto-estado pode ser escrito como o produto de uma função que depende apenas da distância por uma função que depende dos ângulos polar e azimutal. Nesse procedimento, percebe-se que há uma outra grandeza conservada, o momento angular, tornando o momento angular importante para caracterização dos auto-estados do sistema. Classicamente, define-se momento angular como produto vetorial entre posição e momento da partícula: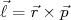 (13)
(13)Podemos usar essa mesma definição como ponto de partida em mecânica quântica, substituindo as componentes dos vetores posição e momento pelos seus operadores correspondentes. Por exemplo, a componente z do momento angular pode ser escrita como:
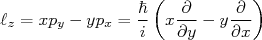 (14)
(14)Vamos calcular
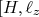 ] para uma Hamiltoniana cujo potencial é central:
] para uma Hamiltoniana cujo potencial é central:
![[H,\ell_z] = \left[\frac{p^2}{2\mu} +V(r), xp_y - yp_x \right] [H,\ell_z] = \left[\frac{p^2}{2\mu} +V(r), xp_y - yp_x \right]](/~suaide/blog/pivotx/extensions/renderlatex/pictures/66cd06724b577d64ccda5a1e6432d5a8.png) (15)
(15)Nesse ponto, e ficará claro porque, as constantes acima não importam. Vamos dividir esse comutador em duas partes:
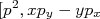 ] e
] e 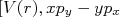 ]:
]:
![[p^2, xp_y - yp_x] = [p_x^2+p_y^2+p_z^2, xp_y-yp_x ] = [p_x^2,xp_y] -[p_y^2,yp_x] [p^2, xp_y - yp_x] = [p_x^2+p_y^2+p_z^2, xp_y-yp_x ] = [p_x^2,xp_y] -[p_y^2,yp_x]](/~suaide/blog/pivotx/extensions/renderlatex/pictures/107093ebf9f9eed2d67ad6b257d9a250.png)
![= p_x[p_x,x]p_y + [p_x,x]p_xp_y - p_y[p_y,y]p_x-[p_y,y]p_yp_x = p_x[p_x,x]p_y + [p_x,x]p_xp_y - p_y[p_y,y]p_x-[p_y,y]p_yp_x](/~suaide/blog/pivotx/extensions/renderlatex/pictures/2e626c0006b420fde3149e54b88dffa5.png)

Vamos agora calcular a segunda parte do comutador:
![[V(r), xp_y - yp_x] = [V,xp_y] - [V,yp_x] = x[V,p_y] - y[V,p_x] [V(r), xp_y - yp_x] = [V,xp_y] - [V,yp_x] = x[V,p_y] - y[V,p_x]](/~suaide/blog/pivotx/extensions/renderlatex/pictures/0937be57c8ae24ead73605b943489fb1.png)
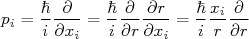
![x[V,p_y] - y[V,p_x] = \frac{\hbar}{i}\left(x\left(V\frac{y}{r} \frac{\partial}{\partial r} - \frac{y}{r} \frac{\partial}{\partial r}V\left) - y\left(V\frac{x}{r} \frac{\partial}{\partial r} - \frac{x}{r} \frac{\partial}{\partial r}V\right) \right) = 0 x[V,p_y] - y[V,p_x] = \frac{\hbar}{i}\left(x\left(V\frac{y}{r} \frac{\partial}{\partial r} - \frac{y}{r} \frac{\partial}{\partial r}V\left) - y\left(V\frac{x}{r} \frac{\partial}{\partial r} - \frac{x}{r} \frac{\partial}{\partial r}V\right) \right) = 0](/~suaide/blog/pivotx/extensions/renderlatex/pictures/07fb18c10dc7384411a10a412304daf2.png)
Ou seja:
![[H,\ell_z] = 0 [H,\ell_z] = 0](/~suaide/blog/pivotx/extensions/renderlatex/pictures/f7b46ca1286896cf391da0d6408f78da.png) (16)
(16)O resultado acima para
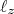 pode ser extendido para as outras componentes, assim
pode ser extendido para as outras componentes, assim ![[H,\ell_i] = 0 [H,\ell_i] = 0](/~suaide/blog/pivotx/extensions/renderlatex/pictures/2a26c21a9418e12de9c7a5e3ca777f7f.png) . Como o momento angular é a soma das suas componentes, podemos dizer que:
. Como o momento angular é a soma das suas componentes, podemos dizer que:
![[H,\ell^2] = 0 [H,\ell^2] = 0](/~suaide/blog/pivotx/extensions/renderlatex/pictures/ebe5b9a7dddc2710be30f2c19f1f9504.png) (17)
(17)E assim, o momento angular é uma constante do movimento sendo, portanto, os seus auto-estados também auto-estados da Hamiltoniana. Nesse caso, podemos usar os seus auto-valores como número quântico para caracterizar um auto-estado da Hamiltoniana. Dos resultados acima pode-se pensar que, como as três componentes do momento angular são constantes do movimento, poderíamos usar os auto-valores dessas três componentes como números quânticos. Isso não é verdade, como será discutido a seguir. Vamos calcular, por exemplo:
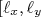 ]:
]:
![[\ell_x,\ell_y] = [yp_z - zp_y, zp_x - xp_z] [\ell_x,\ell_y] = [yp_z - zp_y, zp_x - xp_z]](/~suaide/blog/pivotx/extensions/renderlatex/pictures/1506309bf1fa2fec926f94a127bc17b7.png)
![= [yp_z,zp_x] + [zp_y,xp_z] = y[p_z,z]p_x + x[z,p_z]p_y = [yp_z,zp_x] + [zp_y,xp_z] = y[p_z,z]p_x + x[z,p_z]p_y](/~suaide/blog/pivotx/extensions/renderlatex/pictures/ed49dc806d3ce23a3cff7fd30869a624.png)
![= [yp_z,zp_x] + [zp_y,xp_z] = y(-i\hbar)p_x + x(i\hbar)p_y = [yp_z,zp_x] + [zp_y,xp_z] = y(-i\hbar)p_x + x(i\hbar)p_y](/~suaide/blog/pivotx/extensions/renderlatex/pictures/80155d7b3aee3c6a59ced7b36f29f112.png)
Assim:
![[\ell_x,\ell_y] = i\hbar(xp_y - yp_x ) = i\hbar\ell_z [\ell_x,\ell_y] = i\hbar(xp_y - yp_x ) = i\hbar\ell_z](/~suaide/blog/pivotx/extensions/renderlatex/pictures/37af3af885989b6a3fff8378ce4b8b4c.png) (18)
(18)Ou seja, apesar de haver auto-estados simultâneos da Hamiltoniana e qualquer componente do momento angular, não há auto-estados simultâneos de duas componentes do momento angular. Essa limitação está diretamente relacionada ao princípio de incerteza na qual não podemos medir as três componentes com precisão ilimitada. Contudo, pode-se mostrar que qualquer componente do momento angular comuta com o momento angular lotal, ou seja:
![[\ell_i,\ell^2] =0 [\ell_i,\ell^2] =0](/~suaide/blog/pivotx/extensions/renderlatex/pictures/9841cd1f6820d533897bfd8c22c0a18a.png) (19)
(19)Assim, podemos achar um conjunto de estados quânticos que sejam, simultaneamente, auto-estados da Hamiltoniana, do momento angular e de uma componente do momento angular. Em geral escolhe-se a componente z do momento angular. Esses auto-estados satisfazem as seguintes relações:

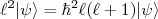 (20)
(20)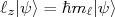
No caso de um potencial central, esses auto-estados são escritos de acordo com a equação (11), de modo que
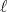 é um número inteiro, maior ou igual a zero, e
é um número inteiro, maior ou igual a zero, e 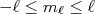 .
.
A partir das relações acima, podemos concluir que cada subconjunto de auto-estados de mesma energia é composto
 auto-estados degenerados de momento angular. Isso de fato ocorre. A princípio, por exemplo, em um sistema atômico (o mesmo vale para sistemas nucleares) um elétron de energia E poderia estar em
auto-estados degenerados de momento angular. Isso de fato ocorre. A princípio, por exemplo, em um sistema atômico (o mesmo vale para sistemas nucleares) um elétron de energia E poderia estar em  estados diferentes de momento angular. Esses níveis de energia, na presença de um campo magnético, se separariam, devido ao acoplamento do momento magnético desse elétron por conta do seu estado de momento angular. Sendo
estados diferentes de momento angular. Esses níveis de energia, na presença de um campo magnético, se separariam, devido ao acoplamento do momento magnético desse elétron por conta do seu estado de momento angular. Sendo  sempre um número ímpar, espera-se que o número de estados observados também seriam ímpares. Esse é o chamado efeito Zeeman. Em alguns átomos, como o átomo de sódio, é observado que essa separação resulta em um número par de estados distintos. Esse fenômeno foi denominado de efeito Zeeman anômalo e intrigou a comunidade científica. Essas observações sugerem a existência de alguma outra propriedade, similar a momento angular, que deve caracterizar esse sistema. Além disso, medidas de níveis de energia atômicos com elevada precisão mostram que há estruturas de energia fina e hiperfina nos níveis de energia dos átomos. Essas estruturas não podem ser explicadas apenas pelas propriedades da Hamiltoniana de potencial central, que dá origem ao momento angular orbital. Essas evidências indicam a necessidade de incorporar uma outra propriedade ao sistema quântico estudado: o spin. Essa propriedade, descoberta experimentalmente, teve seu formalismo desenvolvido inicialmente por Pauli e, posteriormente, de forma mais concisa, por Dirac, através da sua formulação relativística para mecânica quântica.
sempre um número ímpar, espera-se que o número de estados observados também seriam ímpares. Esse é o chamado efeito Zeeman. Em alguns átomos, como o átomo de sódio, é observado que essa separação resulta em um número par de estados distintos. Esse fenômeno foi denominado de efeito Zeeman anômalo e intrigou a comunidade científica. Essas observações sugerem a existência de alguma outra propriedade, similar a momento angular, que deve caracterizar esse sistema. Além disso, medidas de níveis de energia atômicos com elevada precisão mostram que há estruturas de energia fina e hiperfina nos níveis de energia dos átomos. Essas estruturas não podem ser explicadas apenas pelas propriedades da Hamiltoniana de potencial central, que dá origem ao momento angular orbital. Essas evidências indicam a necessidade de incorporar uma outra propriedade ao sistema quântico estudado: o spin. Essa propriedade, descoberta experimentalmente, teve seu formalismo desenvolvido inicialmente por Pauli e, posteriormente, de forma mais concisa, por Dirac, através da sua formulação relativística para mecânica quântica.
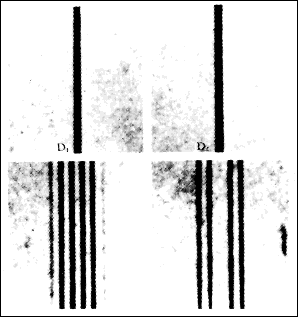
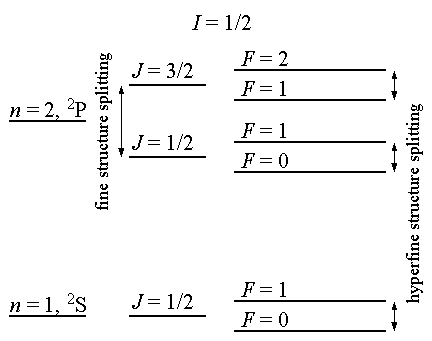
Segundo Pauli, além das propriedades de momento angular espacial, deve-se adicionar propriedades de spin. Os operadores de spin possuem propriedades similares as de momento angular, ou seja:
![[S_x,S_y] = i\hbar S_z [S_x,S_y] = i\hbar S_z](/~suaide/blog/pivotx/extensions/renderlatex/pictures/c629f92410b27f3f360becfda97c0f90.png) e assim por diante
e assim por diante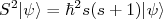 (21)
(21)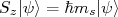
Contudo, nesse caso,
 poderia assumir valores semi-inteiros. Isso é necessário para explicar os efeitos experimentais observados, tomando que
poderia assumir valores semi-inteiros. Isso é necessário para explicar os efeitos experimentais observados, tomando que 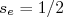 . Além disso, Pauli postulou que o auto-estado final de um sistema com spin seria composto através do produto de auto-estados espaciais e auto-estados de spin, ou seja:
. Além disso, Pauli postulou que o auto-estado final de um sistema com spin seria composto através do produto de auto-estados espaciais e auto-estados de spin, ou seja:
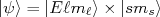 (22)
(22)Uma consequência imediata de (22) é que os operadores de spin comutam com os operadores espaciais (posição e momento) e os observáveis de spin seriam constantes de movimento (assim como momento angular, não é possível medir com precisão infinita as três componentes de spin).
Nesse caso, um estado quântico poderia ser descrito como:
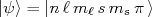 (23)
(23)sendo
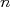 um número quântico que representa o nível de energia e
um número quântico que representa o nível de energia e  a paridade do estado, caso ele possua paridade bem definida.
a paridade do estado, caso ele possua paridade bem definida.
Em geral, sistemas de partículas contendo spin possuem Hamiltoniana com pequenas perturbações devido ao acoplamento do momento magnético dessas partículas, por conta do seu spin, com campos magnéticos que podem ser criados devido ao momento angular orbital. Esse é o chamado acoplamento spin-órbita e será discutido em detalhes mais a frente, quando estudarmos modelo de camadas. Contudo, a Hamiltoniana do sistema passa a possuir um novo termo, devido a esse acoplamento, e assim, escrevemos que a nova Hamiltoniana do sistema vale:
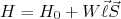 (24)
(24)Nessa situação, pode-se mostrar que os operadores
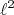 e
e 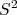 continuam comutando com a Hamiltoniana. Por outro lado, os operadores
continuam comutando com a Hamiltoniana. Por outro lado, os operadores 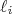 e
e 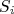 não comutam mais com a Hamiltoniana. Demonstremos isso para o caso do operador
não comutam mais com a Hamiltoniana. Demonstremos isso para o caso do operador 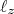 :
:
![[H,\ell_z] = [H_0,\ell_z]+[W\vec{\ell}\vec{S},\ell_z] = [W\vec{\ell}\vec{S},\ell_z] [H,\ell_z] = [H_0,\ell_z]+[W\vec{\ell}\vec{S},\ell_z] = [W\vec{\ell}\vec{S},\ell_z]](/~suaide/blog/pivotx/extensions/renderlatex/pictures/d6e209bb383e0b70ab31339fcf2ec983.png)
Assumindo
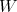 como radial, basta calcular
como radial, basta calcular ![[\vec{\ell}\vec{S},\ell_z] [\vec{\ell}\vec{S},\ell_z]](/~suaide/blog/pivotx/extensions/renderlatex/pictures/dec8c32f76e256cf796434c2dd914ff6.png) , ou seja:
, ou seja:
![[\vec{\ell}\vec{S},\ell_z] = [ \ell_xS_x + \ell_yS_y + \ell_zS_z, \ell_z] [\vec{\ell}\vec{S},\ell_z] = [ \ell_xS_x + \ell_yS_y + \ell_zS_z, \ell_z]](/~suaide/blog/pivotx/extensions/renderlatex/pictures/64ffdb82ac8753752a2f2128d23e7c07.png)
![= [ \ell_x,\ell_z]S_x + [\ell_y,\ell_z]S_y \neq 0 = [ \ell_x,\ell_z]S_x + [\ell_y,\ell_z]S_y \neq 0](/~suaide/blog/pivotx/extensions/renderlatex/pictures/f7b6371793927d2dc53befcc4b9df58f.png) (25)
(25)O mesmo pode-se demonstrar para as outras componentes de momento angular e spin. Desse modo, como essas componentes não mais comutam com a Hamiltoniana, as mesmas deixam de ser constantes de movimento e não podemos escrever estados que sejam simultaneamente auto-estados de
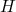 e
e 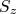 , por exemplo. Desse modo perdemos dois números quânticos que descreveriam o estado do sistema.
, por exemplo. Desse modo perdemos dois números quânticos que descreveriam o estado do sistema.
É conveniente encontrar uma base que possa descrever esse sistema e que também possa descrever o sistema sem esse acoplamento. Isso pode ser feito definindo-se o momento angular total como sendo:
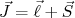 (26)
(26)Esse operador satisfaz todas relações de comutação e auto-valores de um operador de momento angular, ou seja:
![[J_x,J_y] = i\hbar J_z [J_x,J_y] = i\hbar J_z](/~suaide/blog/pivotx/extensions/renderlatex/pictures/80b98056e8574e30b821f1460d581ca6.png) e assim por diante
e assim por diante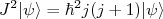 (27)
(27)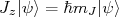
Pode-se demonstrar que
![[H,J^2] = 0 [H,J^2] = 0](/~suaide/blog/pivotx/extensions/renderlatex/pictures/ef2be719e75449819eba6d9759776a04.png) e que
e que ![[H, J_z] = 0 [H, J_z] = 0](/~suaide/blog/pivotx/extensions/renderlatex/pictures/364308afec0650f70e09e7d3c4440cd0.png) (exercícios), sendo, assim, constantes do movimento. Desse modo, é muito mais conveniente representar auto-estados de sistemas com momento angular orbital e spin atraves de:
(exercícios), sendo, assim, constantes do movimento. Desse modo, é muito mais conveniente representar auto-estados de sistemas com momento angular orbital e spin atraves de:
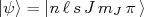 (28)
(28)Em muitas situações práticas, contudo, a descrição do sistema em termos das projeções de momento angular orbital e spin ainda são desejáveis. Nesse caso, precisa-se expandir um estado de momento angular total em estados de momento angular e spin. Usamos a expansão:
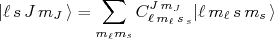 (29)
(29)onde os coeficientes
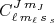 são chamados de coeficientes de Clebsch–Gordan e os seus valores podem ser obtidos de tabelas (um bom livro de Mecânica Quântica contém tabelas para esses coeficientes) ou calculados. Uma propriedade importante vem do fato de
são chamados de coeficientes de Clebsch–Gordan e os seus valores podem ser obtidos de tabelas (um bom livro de Mecânica Quântica contém tabelas para esses coeficientes) ou calculados. Uma propriedade importante vem do fato de 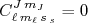 se
se 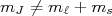 , o que reduz consideravelmente as combinações de estados necessárias para descrever um estado em uma base ou outra.
, o que reduz consideravelmente as combinações de estados necessárias para descrever um estado em uma base ou outra.
Em física nuclear, tanto o spin do próton como do nêutron possuem valor 1/2. Nesse caso, é implícito o valor de
 em (28). Costuma-se também utilizar a notação espectroscópica para designar um estado quântico de um núcleon ou até mesmo um núcleo, já que os momentos angulares de um sistema de nucleons correspondem à soma dos momentos angulares dos seus constituintes. A notação espectroscópica consiste em utilizar:
em (28). Costuma-se também utilizar a notação espectroscópica para designar um estado quântico de um núcleon ou até mesmo um núcleo, já que os momentos angulares de um sistema de nucleons correspondem à soma dos momentos angulares dos seus constituintes. A notação espectroscópica consiste em utilizar:
 (30)
(30)Sendo
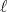 subsitituído por letras (s, p, d, f, ...) de acordo com o seu valor. Como, em geral, os auto-estados de energia são degenerados em
subsitituído por letras (s, p, d, f, ...) de acordo com o seu valor. Como, em geral, os auto-estados de energia são degenerados em 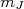 , é comum omití-lo da notação. Também é o caso quando a paridade é definida apenas pelo momento angular orbital. Como exemplo, o estado com
, é comum omití-lo da notação. Também é o caso quando a paridade é definida apenas pelo momento angular orbital. Como exemplo, o estado com 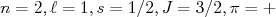 pode ser representado como
pode ser representado como 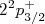 . Em algumas notações o termo
. Em algumas notações o termo 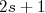 , superescrito, não aparece. Esse termo designa qual a multiplicidade do estado de spin (singleto, dubleto, tripleto, etc.) e é mais comum de aparecer caso haja mais de uma partícula envolvida. Há varias outras formas de notação. Por exemplo, também é comum representar o estado usando a notação
, superescrito, não aparece. Esse termo designa qual a multiplicidade do estado de spin (singleto, dubleto, tripleto, etc.) e é mais comum de aparecer caso haja mais de uma partícula envolvida. Há varias outras formas de notação. Por exemplo, também é comum representar o estado usando a notação  . No exemplo anterior, teríamos o estado
. No exemplo anterior, teríamos o estado 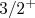 .
.
A situação para o núcleo atômico poderia ser bastante complexa: cada nucleon, além do seu spin (1/2) pode possuir momento angular orbital, cuja soma resulta no momento angular total do nucleon. O momento angular total do núcleo é a soma de todos os momentos angulares totais de cada nucleon. Nesse caso, calcular o momento angular total de um núcleo envolveria uma complexa combinação de possibilidades de soma. Costuma-se utilizar a letra
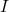 para representar o momento angular total do núcleo atômico. Contudo, o problema é drasticamente simplificado com base em algumas observações:
para representar o momento angular total do núcleo atômico. Contudo, o problema é drasticamente simplificado com base em algumas observações:
- O momento angular total de um nucleon, por ser a soma do seu spin (1/2) com o momento angular orbital (sempre um número inteiro), possui valores sempre semi-inteiros (
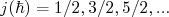 ). Desse modo, a componente-z do momento angular total de um nucleon é semi-inteiro.
). Desse modo, a componente-z do momento angular total de um nucleon é semi-inteiro.
- Como o momento angular total do núcleo
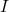 é a soma dos momentos angulares individuais, caso o núcleo seja par, essa soma será sempre um valor inteiro. Caso o núcleo seja ímpar, o momento angular total é semi-inteiro. Assim:
é a soma dos momentos angulares individuais, caso o núcleo seja par, essa soma será sempre um valor inteiro. Caso o núcleo seja ímpar, o momento angular total é semi-inteiro. Assim:
- Para núcleos pares,
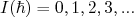
- Para núcleos ímpares,
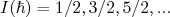
- Para núcleos pares,
- Medidas de momento angular para núcleos par-par (Z e N pares) no seu estado fundamental mostram que todos esses núcleos possuem momento angular total
 . Essa informação é extremamente importante pois permite a conclusão que nucleons tendem a se emparelhar em termos de momento angular, aumentando a sua estabilidade. Essa evidência, de certa forma, já se fez presente na fórmula de massa, quando observamos que núcleos par-par são mais estáveis.
. Essa informação é extremamente importante pois permite a conclusão que nucleons tendem a se emparelhar em termos de momento angular, aumentando a sua estabilidade. Essa evidência, de certa forma, já se fez presente na fórmula de massa, quando observamos que núcleos par-par são mais estáveis.
- Como consequência da observação anterior, o momento angular de um núcleo ímpar é sempre o momento angular do nucleon que não foi emparelhado. Para um núcleo par, porém ímpar-ímpar, o momento angular do núcleo consiste da soma dos momentos angulares dos dois nucleons que não se encontram emparelhados, ou seja,
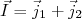 .
.
- Por conta da complexidade do sistema de soma de momentos angulares, não é possível fazer uma correlação unívoca entre o momento angular total de um núcleo e a sua paridade. Apesar de núcleos possuirem paridade bem definida, um estado de momento angular par pode possuir tanto paridade positiva quanto negativa.
Isospin
Prótons e nêutrons possuem quase a mesma massa. Além disso, evidências experimentais sugerem que a interação forte não depende da carga elétrica. Na figura 4 é mostrado o esquema de níveis de energia para o 23Na e 23Mg. A diferença entre esses núcleos é de um próton e um nêutron, ou seja, há apenas a troca de um próton por um nêutron entre eles. Nesses níveis de energia já foram descontados as componentes devido à interação coulombiana e diferença de massa entre os núcleos, ou seja, o esquema apresentado reflete a interação nuclear forte entre os nucleons. Pode-se notar uma compatibilidade muito grande entre os níveis de energia. Essa semelhança também está presente em outras partículas. Por exemplo, o píon apresenta 3 estados de carga (π0, π+ e π-), quase todos com a mesma massa e interação forte independente da carga elétrica. Podemos encontrar vários outros exemplos similares.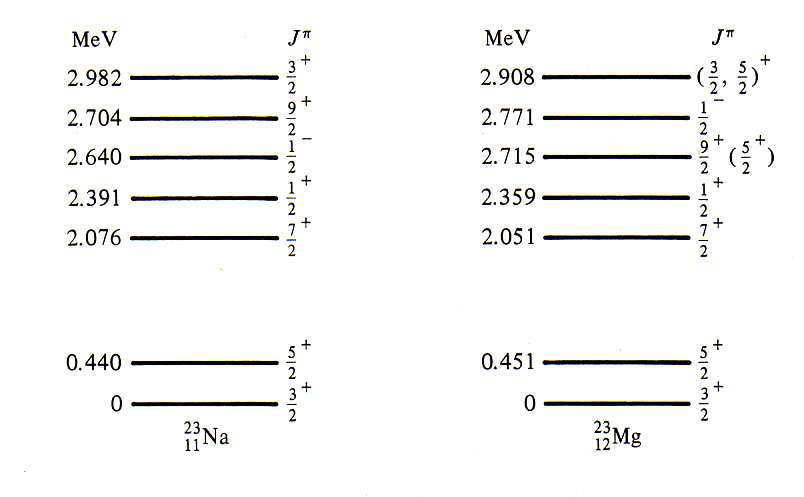
Heisenberg, em 1932, sugeriu que, do ponto de vista da interação forte, poderíamos tratar essas partículas como sendo estados quânticos diferentes de uma mesma partícula (não que sejam de fato). No caso do próton e nêutron, seria uma partícula (chamada nucleon) com dois estados quânticos. No caso dos píons, teríamos uma partícula, píon, em três estados quânticos distintos. Para representar essa propriedade, introduzimos o conceito de isospin, ou spin de carga. Nesse caso, os operadores de isospin são definidos com algebra idêntica àquela para momento angular, ou seja:
![[T_x,T_y] = i\hbar T_z [T_x,T_y] = i\hbar T_z](/~suaide/blog/pivotx/extensions/renderlatex/pictures/4a281fecbc27c5af86d3fdce96e09e1a.png) e assim por diante
e assim por diante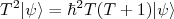 (31)
(31)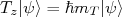
No caso dos nucleons, temos um sistema de dois níveis,
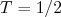 , sendo escolhido que
, sendo escolhido que 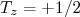 para o próton e
para o próton e 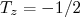 para nêutrons (alguns livros usam notação invertida, cuidado!). No caso do píon,
para nêutrons (alguns livros usam notação invertida, cuidado!). No caso do píon,  , que possui três estados para a projeção no eixo-z,
, que possui três estados para a projeção no eixo-z,  , atribuído a cada um dos píons observados.
, atribuído a cada um dos píons observados.
Em um sistema de muitos nucleons, valem as regras de adição vetorial. Em um sistema de dois nucleons, temos três combinações possíveis: próton-próton, próton-nêutron e nêutron-nêutron. No primeiro,
 de modo que o isospin desse sistema vale
de modo que o isospin desse sistema vale  . No último,
. No último,  de modo que o isospin desse sistema vale
de modo que o isospin desse sistema vale  , assim como no caso próton-próton. No caso do sistema próton-nêutron,
, assim como no caso próton-próton. No caso do sistema próton-nêutron,  , o que nos dá duas possibilidades para o isospin:
, o que nos dá duas possibilidades para o isospin:  ou
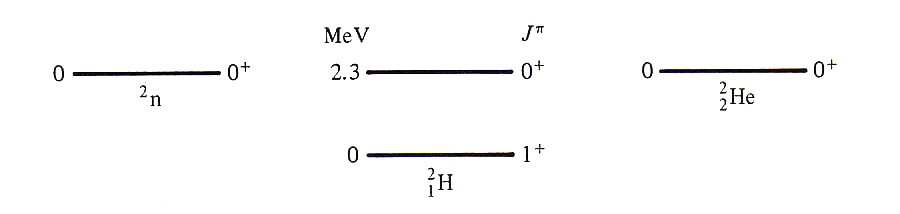
ou  . Na figura 5 mostramos o esquema de níveis de energia de estados de dois nucleons, após descontarmos a energia coulombiana e a diferença de massas. Note que o estado
. Na figura 5 mostramos o esquema de níveis de energia de estados de dois nucleons, após descontarmos a energia coulombiana e a diferença de massas. Note que o estado  corresponde a um tripleto, ou seja, um estado de isospin 1, enquanto o estado
corresponde a um tripleto, ou seja, um estado de isospin 1, enquanto o estado  , só presente no dêuteron, por ser um singleto, possui isospin 0. A independência da carga na interação forte pode ser resumida em tomar que a interação depende somente do isospin total do estado e não de sua componente em z. Isso é bastante similar a estados de momento angular e spin.
, só presente no dêuteron, por ser um singleto, possui isospin 0. A independência da carga na interação forte pode ser resumida em tomar que a interação depende somente do isospin total do estado e não de sua componente em z. Isso é bastante similar a estados de momento angular e spin.
O conceito de isospin é muito importante em física nuclear e de partículas. Veremos que o isospin é um número quântico a ser conservado em decaimentos e reações nucleares, servindo como regra de seleção para esses processos.
Exercícios
- Mostre que se o potencial de interação é uma função par nas coordenadas,
![[H,P]=0 [H,P]=0](/~suaide/blog/pivotx/extensions/renderlatex/pictures/60c4aca9d91076fa7dda4c18dea95ece.png) .
.
- Mostre que, mesmo havendo um termo de acoplamento spin-órbina na Hamiltoniana,
![[H,\ell^2] = 0 [H,\ell^2] = 0](/~suaide/blog/pivotx/extensions/renderlatex/pictures/ebe5b9a7dddc2710be30f2c19f1f9504.png) e
e ![[H, S^2] = 0 [H, S^2] = 0](/~suaide/blog/pivotx/extensions/renderlatex/pictures/48e7fb0c19f1f312ae46086ca0b83696.png) .
.
- Mostre que, mesmo havendo um termo de acoplamento spin-órbina na Hamiltoniana,
![[H,J^2] = 0 [H,J^2] = 0](/~suaide/blog/pivotx/extensions/renderlatex/pictures/ef2be719e75449819eba6d9759776a04.png) e
e ![[H, J_z] = 0 [H, J_z] = 0](/~suaide/blog/pivotx/extensions/renderlatex/pictures/364308afec0650f70e09e7d3c4440cd0.png) .
.
- Em um sistema de dois nucleons, obtenha os possíveis valores de momento angular total,
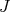 , supondo que o estado esteja esteja em um nível
, supondo que o estado esteja esteja em um nível 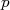 de momento angular orbital. Quantos estados seriam possíveis nesse caso?
de momento angular orbital. Quantos estados seriam possíveis nesse caso?
Leitura recomendada
- Introductory Nuclear Physics, K. S. Krane, capítulo 3.4.
- Introdução à Física Nuclear, H. Schechter e C. A. Bertulani, capítulos 1.5, 1.6 e 3.4.
- Fundamentals of Nuclear Physics, N. A. Jelley, capítulo 1.4.
- Quantum Mechanics, C. Cohen-Tannoudji et al., capítulos VI, IX e X.




No comments