Decaimento β
Notas de aula são propriedade intelectual. Sendo assim, qualquer uso, no todo ou em parte, deve ter a origem referenciada apropriadamente, após autorização de seu autor.
O texto a seguir corresponde à anotações parciais de aula. Não é um texto em forma final, completo e totalmente revisado. Nesse caso, esse texto não tem como objetivo substituir livros sobre o assunto. Assim, esse texto deve ser entendido apenas como um guia de estudo para o aluno acompanhar a disciplina.
A emissão β consiste no principal mecanismo de decaimento de núcleos fora da linha de estabilidade. Isso por conta da pequena massa da partícula β, se comparada às massas nucleares, tornando os limiares de emissão menores que aqueles para emissão de partículas mais pesadas. No decaimento β um próton se converte em nêutron, emitindo um pósitron (β+). O processo inverso pode ocorrer, um nêutron decaindo em próton, emitindo um elétron (β-). Há ainda a captura eletrônica, na qual um elétron é capturado pelo núcleo, convertendo um próton em nêutron. Assim, os processos básicos nucleares envolvidos nesses três decaimentos são:
 (1)
(1) (2)
(2) (3)
(3)Apesar dos decaimentos acima estarem corretos, com a presença do neutrino, o entendimento dessas reações não era completo no início dos estudos de decaimentos nucleares. Não se sabia da existência do neutrino e, mesmo após ser postulado, foi necessário décadas para medí-lo. As evidências experimentais obtidas do decaimento β eram tão intrigantes que o completo entendimento do mesmo levou muito tempo para ocorrer, ao contrário do decaimento α, que consiste de um problema simples de tunelamento quântico.
A primeira evidência intrigante no decaimento β surgiu da medida do espectro de energia para os elétrons emitidos. Em um decaimento genérico de dois corpos
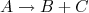 , com o núcleo mãe em repouso, podemos escrever que o valor-Q da reação está relacionado às energias cinéticas das partículas filhas através de:
, com o núcleo mãe em repouso, podemos escrever que o valor-Q da reação está relacionado às energias cinéticas das partículas filhas através de:
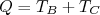 (4)
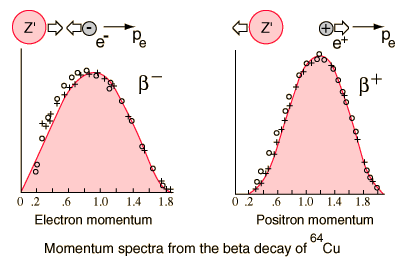
(4)Devemos impor a conservação de momento linear. A conservação do momento em decaimentos de dois corpos, aliado à (4), faz com que as energias cinéticas das partículas filhas sejam bem definidas. Ademais, no decaimento β a massa do elétron é muito menor que a massa do núcleo resultante de decaimento. Nesse caso, toda energia liberada pelo decaimento deveria ser convertida em energia cinética do elétron, igual ao valor-Q da reação, como observa-se, por exemplo, para o decaimento α, em primeira aproximação. Não foi isso o observado. Na figura 1 mostramos o espectro de elétrons (e pósitrons) medidos para o decaimento β do núcleo de 64Cu. A diferença entre os dados para elétrons e pósitrons vem, em uma visão mais ingênua, do fato de elétrons serem freados após o decaimento devido à interação atrativa com o núcleo resultante enquanto pósitrons são repelidos, pelo mesmo motivo. A energia cinética das partículas β emitidas apresenta uma larga distribuição, incompatível com o previsto para um decaimento de dois corpos. Esse foi um grande problema para a física nuclear no início do século XX. Para solucionar esse problema, havia apenas três alternativas:
- Propor que a lei de conservação de energia funciona apenas na média. Essa idéia foi proposta por Niels Bohr.
- Abandona-se a lei de conservação de energia. Isso seria realmente uma quebra gigantesca de paradigma na física e teria sérias consequências para o entendimento da Natureza. Contudo, como se vivia um período bastante conturbado na física, com o início da Mecância Quântica e observação de um mundo microscópico totalmente não intuitivo, essa opção foi considerada por muitos cientistas.
- Propõe-se algo novo, inusitado, que reconcilia as observações com os paradigmas vigentes.
Em 1930, Wolfgang Pauli, em carta submetida a cientistas em uma conferência (figura 2), sugere a existência de uma terceira partícula nesse decaimento. Naquele momento, Pauli chamou essa partícula de nêutron. A descoberta do nêutron por Chadwick, em 1932, com características diferentes das propostas por Pauli, renomeou essa partícula para neutrino. Em tradução (Phillippe Gouffon), temos: "Prezados senhoras e senhores radioativos. Rogo-lhes escutar com muita boa vontade o portador desta carta. Ele lhes dirá em detalhes que, para sanar a má estatística dos núcleos do N e Li6 e o espectro beta contínuo, descobri um remédio desesperado para salvar as leis de conservação da energia e as estatísticas. Trata-se da possibilidade da existência nos núcleos de partículas neutras de spin 1/2, obedecendo ao principio de exclusão, mas diferentes dos fótons pois elas não se movem à velocidade da luz, e que chamo de nêutrons. A massa dos nêutrons deve ser da mesma ordem de grandeza da dos elétrons e não deve em hipótese nenhuma exceder 0,01 da massa do próton. O espectro beta seria então compreensível se supusermos que durante a desintegração beta, com cada elétron emitido um nêutron seja emitido, de modo que a soma das energias do nêutron e do elétron seja constante."

Entre a previsão e descoberta passaram-se mais de 30 anos. Neutrinos foram descobertos apenas em 1953, por Reines e Cowan, que ganharam Prêmio Nobel, mais de 40 anos depois, em 1995. Eles usaram como fonte de neutrinos um reator nuclear e como detector, cintilador líquido rico em prótons. De fato, eles observaram a reação inversa
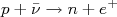 . Nesse primeiro experimento, a razão de sinal para fundo era de 1/10. Medidas mais precisas, alguns anos depois, com razão sinal/fundo de 4/1, confirmaram essa descoberta. A dificuldade em realizar essa medida vem do fato de neutrinos interagirem apenas por força fraca. De fato, neutrinos podem atravessar a Terra sem sofrer, na maioria das vezes, uma única interação. Medidas experimentais do espectro de energia de elétrons sugerem que neutrinos possuam massa muito pequena, se comparada à própria massa do elétron, inicialmente pensada até como nula. A observação da flutuação de neutrinos, que resolveu o problema de neutrinos solares, no início do século XXI, é uma evidência fundamental para a existência de massa não nula para essas partículas. Voltaremos a esse assunto um pouco adiante. Vamos inicialmente formular uma teoria para descrever o decaimento β do núcleo.
. Nesse primeiro experimento, a razão de sinal para fundo era de 1/10. Medidas mais precisas, alguns anos depois, com razão sinal/fundo de 4/1, confirmaram essa descoberta. A dificuldade em realizar essa medida vem do fato de neutrinos interagirem apenas por força fraca. De fato, neutrinos podem atravessar a Terra sem sofrer, na maioria das vezes, uma única interação. Medidas experimentais do espectro de energia de elétrons sugerem que neutrinos possuam massa muito pequena, se comparada à própria massa do elétron, inicialmente pensada até como nula. A observação da flutuação de neutrinos, que resolveu o problema de neutrinos solares, no início do século XXI, é uma evidência fundamental para a existência de massa não nula para essas partículas. Voltaremos a esse assunto um pouco adiante. Vamos inicialmente formular uma teoria para descrever o decaimento β do núcleo.
A teoria de Fermi para decaimento β
Em 1934 Fermi propôs uma teoria para o decaimento β. Essa teoria não é completa. Por exemplo, naquela época não se sabia sobre violação de paridade nos decaimentos β, só descoberta décadas mais tarde. Contudo, podemos explicar vários aspectos do decaimento β, tais como constantes de decaimento e espectros de energia das partículas emitidas. Naquela época eram conhecidos os decaimentos α e γ do núcleo. O decaimento α consiste em um simples problema de tunelamento quântico e não é possível aplicá-lo nesse caso. As razões são simples: a partícula β e neutrino não existem dentro do núcleo. Essa teoria deve ser capaz de explicar suas formações. No caso do decaimento β- não há barreira para tunelamento. No caso β+ pode-se mostrar que, por conta da massa da partícula, a probabilidade de tunelamento é próxima da unidade. Assim, o modelo para decaimento α não é aplicável. Além disso, devemos levar em conta que as partículas β e neutrinos devem ser tratados relativisticamente. As baixas massas dessas partículas fazem com que, nas energias típicas envolvidas, suas velocidades sejam muito altas.Fermi supôs que a interação responsável pelo decaimento β seja fraca e de curta duração, se comparada às constantes de decaimento envolvidas. Nesse caso, pode-se usar como base para construção dessa teoria a regra de ouro de Fermi, já deduzida:
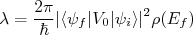 (5)
(5)onde
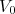 é a parte estática do potencial de interação e
é a parte estática do potencial de interação e 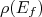 corresponde à densidade de estados finais envolvidos, já que elétrons e neutrinos podem assumir um contínuo de energias. Podemos escrever essa densidade de estados como sendo
corresponde à densidade de estados finais envolvidos, já que elétrons e neutrinos podem assumir um contínuo de energias. Podemos escrever essa densidade de estados como sendo 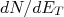 , ou seja, o número de estados possíveis para o intervalo de energia de desintegração entre
, ou seja, o número de estados possíveis para o intervalo de energia de desintegração entre 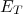 e
e  . Simplificando a notação para o elemento de matriz, de modo que
. Simplificando a notação para o elemento de matriz, de modo que 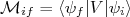 , temos que:
, temos que:
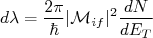 (6)
(6)A mudança de
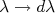 vem do fato que a constante de decaimento é medida independentemente da energia da partícula β e, nesse caso, estamos calculando a constante de decaimento para momentos específicos da partícula β e neutrino. O cálculo da constante de decaimento em (6), para ser realizado, depende do conhecimento das funções de onda inicial e final, da densidade de estados e do potencial de interação. Vamos discutir cada um deles em separado.
vem do fato que a constante de decaimento é medida independentemente da energia da partícula β e, nesse caso, estamos calculando a constante de decaimento para momentos específicos da partícula β e neutrino. O cálculo da constante de decaimento em (6), para ser realizado, depende do conhecimento das funções de onda inicial e final, da densidade de estados e do potencial de interação. Vamos discutir cada um deles em separado.
A função de onda inicial é a função de onda do núcleo original. Já discutimos um pouco sobre isso. Podemos utilizar, por exemplo, o modelo de camadas para obter a função de onda do núcleo original. A função de onda final, por outro lado, envolve três partículas distintas: o núcleo final, a partícula β e o (anti)neutrino. Nesse caso, podemos escrever que a função de onda do estado final é:
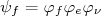 (7)
(7)onde
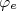 corresponde à função de onda do (elétron)pósitron e
corresponde à função de onda do (elétron)pósitron e 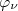 corresponde à função de onda do (anti)neutrino.
corresponde à função de onda do (anti)neutrino. 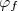 corresponde à função de onda do núcleo final. As funções de onda da partícula β e neutrino podem ser assumidas como aquelas para partículas livres de momentos
corresponde à função de onda do núcleo final. As funções de onda da partícula β e neutrino podem ser assumidas como aquelas para partículas livres de momentos 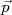 e
e 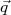 , respectivamente. Como essas funções precisam ser normalizadas, adotaremos um volume
, respectivamente. Como essas funções precisam ser normalizadas, adotaremos um volume 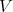 para normalização, de modo que:
para normalização, de modo que:
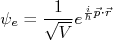 (8)
(8)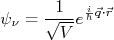 (9)
(9)(8) e (9) podem ser expandidas em:
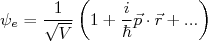 (10)
(10)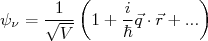 (11)
(11)Levando em consideração o comprimento de onda típico dessas partículas vemos que em volumes típicos de dimensões nucleares, podemos assumir que a função de onda é constante e tomar apenas o primeiro termo das expansões acima. Por exemplo, um elétron de 1 MeV de energia possui comprimento de onda da ordem de 900 fm, muito maior que dimensões típicas nucleares. Se tomarmos, por exemplo, a expansão em ondas parciais de uma onda plana, vemos que esse primeiro termo corresponde ao termo de momento angular orbital
 . Transições com
. Transições com  são denominadas transições permitidas. Cada termo subsequente consiste em um outro termo de momento angular orbital e são denominados de transições proibidas. Essa denominação é enganosa pois induz ao leitor que transições desse tipo não ocorrem, o que não é o caso. Essas contribuições são, a princípio, pequenas, apesar de haver casos nos quais o termo de
são denominadas transições permitidas. Cada termo subsequente consiste em um outro termo de momento angular orbital e são denominados de transições proibidas. Essa denominação é enganosa pois induz ao leitor que transições desse tipo não ocorrem, o que não é o caso. Essas contribuições são, a princípio, pequenas, apesar de haver casos nos quais o termo de  se anula no cálculo do elemento de matriz da transição, sendo necessário considerar os demais termos da expansão.
se anula no cálculo do elemento de matriz da transição, sendo necessário considerar os demais termos da expansão.
Vamos calcular, agora, a densidade de níveis no estado final. Para isso, vamos utilizar a densidade de estados de um gás de férmions. Utilizando da densidade de estados obtidos anteriormente, quando desenvolvemos o modelo de Fermi nuclear, temos, para partículas β e neutrinos, sabendo que
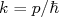 :
:
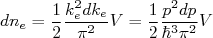 (12)
(12)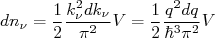 (13)
(13)O número total de estados finais (
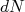 ) pode ser dado pelo produto de (12) e (13). Substituindo esse resultado em (6), chegamos à:
) pode ser dado pelo produto de (12) e (13). Substituindo esse resultado em (6), chegamos à:
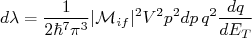 (14)
(14)Desprezando o recuo do núcleo filho, a energia final é dada pela soma das energias da partícula β e neutrino. Supondo a massa do neutrino nula, podemos fazer que
 , de modo a, para uma energia bem definida da partícula β:
, de modo a, para uma energia bem definida da partícula β:
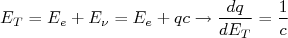 (15)
(15)o que resulta em:
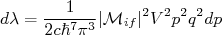 (16)
(16)A partir do valor-Q da reação, podemos escrever que:
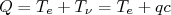
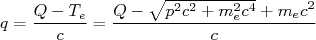 (17)
(17)que, substituindo em (16) obtém-se:
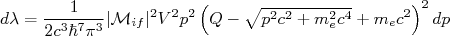 (18)
(18)Vamos fazer um breve comentário sobre o elemento de matriz
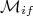 em (18). Esse termo depende da função de onda inicial e final do sistema, bem como do potencial de interação. Tomando apenas a transição permitida, ou seja, o primeiro termo de (10) e (11), podemos fazer:
em (18). Esse termo depende da função de onda inicial e final do sistema, bem como do potencial de interação. Tomando apenas a transição permitida, ou seja, o primeiro termo de (10) e (11), podemos fazer:
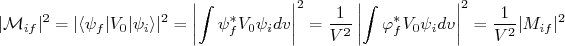 (19)
(19)onde, nesse caso:
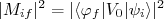 (20)
(20)é o elemento de matriz devido somente às funções de onda nucleares, já que a função de onda inicial é puramente nuclear. Voltaremos a esse assunto mais adiante. Nesse caso, podemos reescrever (18) como:
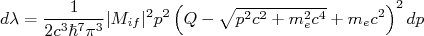 (21)
(21)que não mais depende do volume utilizado para normalizar as funções de onda das partículas β e neutrino. De fato, esse cancelamento ocorre independente do termo adotado na expansão realizada em (10) e (11) e não precisaríamos do artifício de usar somente o termo de transição permitida.
Como o número de partículas β observadas em um intervalo entre
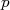 e
e 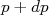 é proporcional à constante de decaimento
é proporcional à constante de decaimento  para esse intervalo, a forma espectral para emissão de parículas β pode ser obtida diretamente de (21), ou seja:
para esse intervalo, a forma espectral para emissão de parículas β pode ser obtida diretamente de (21), ou seja:
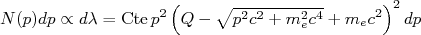 (22)
(22)Na figura 3 vemos um cálculo do espectro de momento de elétrons, a partir de (22), para um decaimento no qual
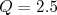 MeV. Temos também o mesmo cálculo para o espectro de energia dos elétrons para esse mesmo valor-Q.
MeV. Temos também o mesmo cálculo para o espectro de energia dos elétrons para esse mesmo valor-Q.
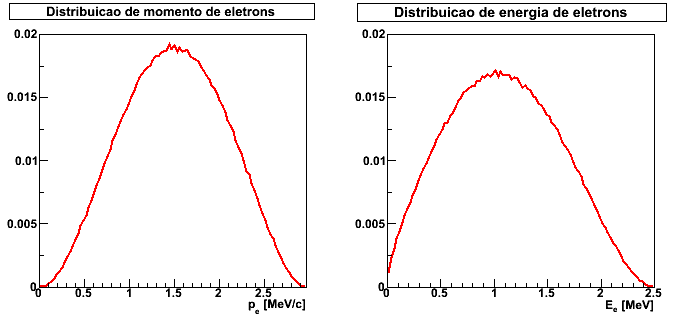
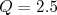 MeV.
MeV.Os espectros apresentados na figura 3 independem se o decaimento é β+ ou β-. Contudo, nos dados mostrados na figura 1 (para espectro de momentos) notamos uma clara diferença entre esses dois decaimentos para o cobre. Argumentamos que isso seria devido à interação da partícula β emitida e o núcleo. Essa interação seria atrativa para o caso da emissão β- e repulsiva para emissão β+. Do ponto de vista mais atual, levando em conta efeitos quânticos, não podemos tratar as funções de onda para as partículas β como sendo ondas planas, por conta da interação coulombiana com o núcleo, de longo alcance. Isso não ocorre no caso dos neutrinos. Esse efeito deve ser levando em consideração para a obtenção do espectro de emissão de elétrons. Esse efeito, de foma mais clara, pode ser visto na figura 4, onde mostramos os espectros em energia e momento para o decaimento β do cobre.
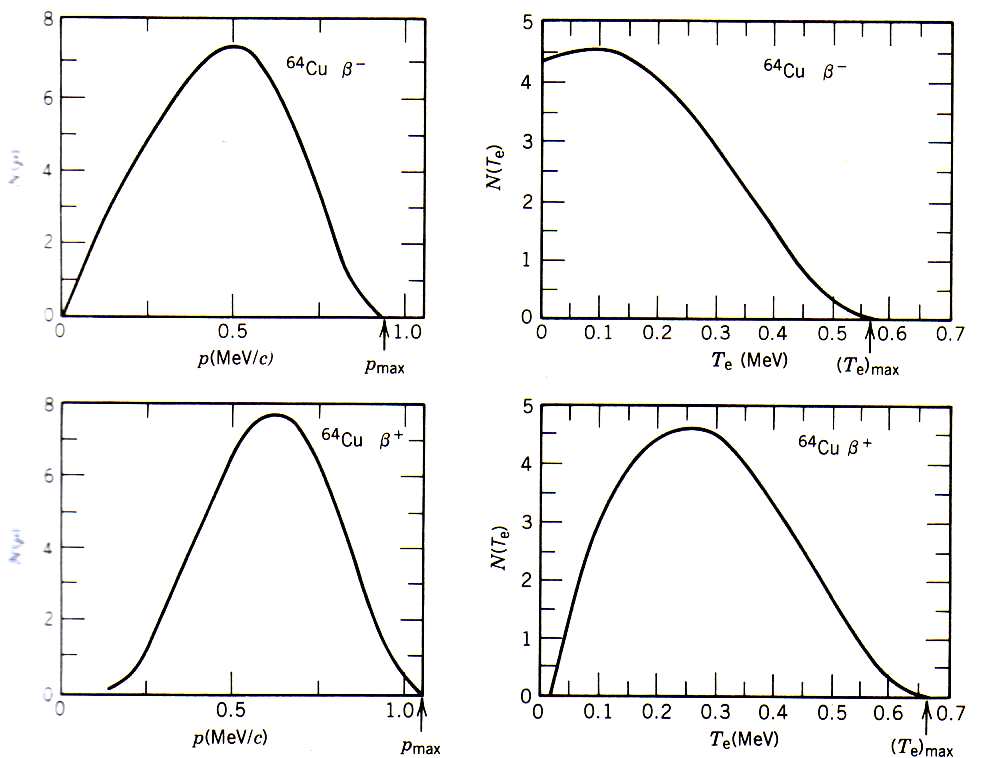
Em sua teoria de 1934, Fermi inclui essa correção devido a essa interação residual entre a partícula β e o núcleo filho, que distorce a função de onda dessa partícula. Podemos fazer isso incluindo um fator de correção em (22). Esse fator, conhecido como Função de Fermi, depende do número atômico do núcleo filho e do momento (ou energia) do elétron ou pósitron, normalmente representada por
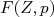 ou
ou 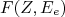 .
.  em (21) e, consequentemente,
em (21) e, consequentemente,  em (22) são modificadas por essa função, cuja dependência com momento ou energia, altera a forma do espectro teórico. No caso de (21), devemos reescrever essa expressão como:
em (22) são modificadas por essa função, cuja dependência com momento ou energia, altera a forma do espectro teórico. No caso de (21), devemos reescrever essa expressão como:
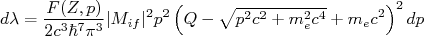 (23)
(23)A dedução de
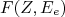 é um processo tedioso e complexo, que envolve o cálculo relativístico das interações dessas partículas com o campo coulombiano do núcleo. Esse cálculo foi apresentado por E. Fermi, em 1934 (ver leitura recomendada). A expressão final para
é um processo tedioso e complexo, que envolve o cálculo relativístico das interações dessas partículas com o campo coulombiano do núcleo. Esse cálculo foi apresentado por E. Fermi, em 1934 (ver leitura recomendada). A expressão final para 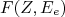 é bastante complexa e difícil de calcular. Normalmente utilizam-se valores tabelados ou gráficos para essa função. Muitos outros cálculos foram desenvolvidos ao longo das décadas seguintes na tentativa de simplificar
é bastante complexa e difícil de calcular. Normalmente utilizam-se valores tabelados ou gráficos para essa função. Muitos outros cálculos foram desenvolvidos ao longo das décadas seguintes na tentativa de simplificar 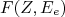 . Em 1985, Venkataramaiah et. al fizeram um estudo sistemático dessas várias parametrizações e chegaram a uma função empírica para
. Em 1985, Venkataramaiah et. al fizeram um estudo sistemático dessas várias parametrizações e chegaram a uma função empírica para 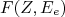 , com base em ajustes de valores tabelados diversos para a função de Fermi (ver leitura recomendada). Assim mesmo, a expressão original deduzida por Fermi é:
, com base em ajustes de valores tabelados diversos para a função de Fermi (ver leitura recomendada). Assim mesmo, a expressão original deduzida por Fermi é:
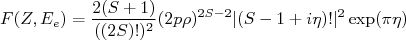 (24)
(24)com
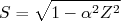 ,
, 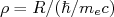 e
e 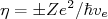 .
.  é a constante de estrutura fina,
é a constante de estrutura fina,  é o número atômico do núcleo residual,
é o número atômico do núcleo residual, 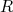 é o raio do núcleo residual e
é o raio do núcleo residual e 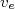 , a velocidade do elétron. O sinal de
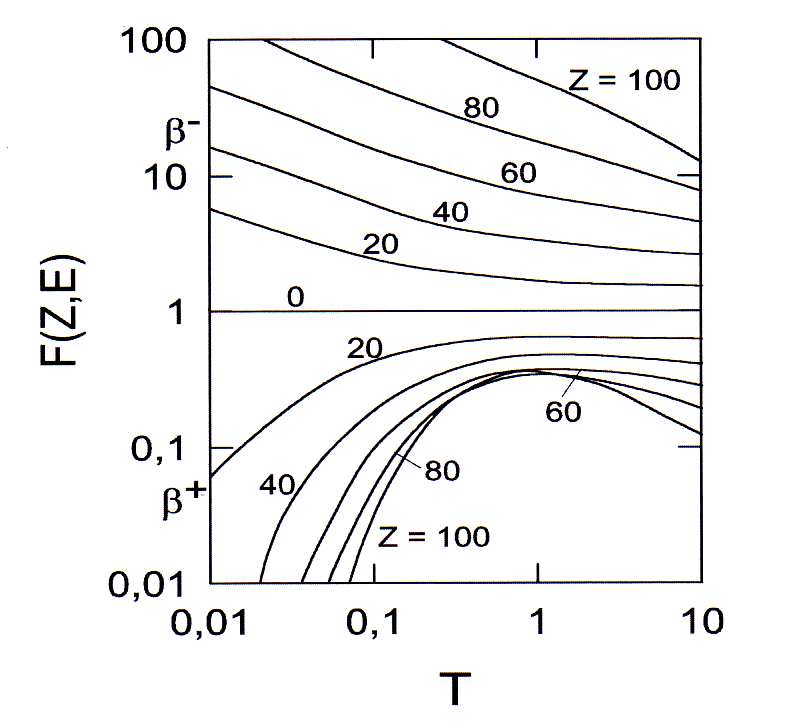
, a velocidade do elétron. O sinal de 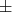 distingue pósitrons de elétrons, sendo positivo para elétrons. A figura 5 mostra algumas dessas funções para alguns núcleos.
distingue pósitrons de elétrons, sendo positivo para elétrons. A figura 5 mostra algumas dessas funções para alguns núcleos.
Vamos voltar a nossa atenção agora sobre o elemento de matriz
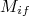 . Esse elemento de matriz contém informação acerca do potencial de interação que viabiliza a transição entre um estado nuclear para outro. No nosso caso, tomamos apenas o termo denominado de transição permitida, de modo que esse elemento de matriz depende somente das funções de onda nucleares inicial e final. No modelo proposto por Fermi, o potencial de interação fraco, responsável pelo decaimento β, foi tomado de forma bastante simples, sem levar em consideração possíveis efeitos relativísticos e de spin das partículas envolvidas. A forma mais simples de escrever o coeficiente de transmissão, nesse caso, é:
. Esse elemento de matriz contém informação acerca do potencial de interação que viabiliza a transição entre um estado nuclear para outro. No nosso caso, tomamos apenas o termo denominado de transição permitida, de modo que esse elemento de matriz depende somente das funções de onda nucleares inicial e final. No modelo proposto por Fermi, o potencial de interação fraco, responsável pelo decaimento β, foi tomado de forma bastante simples, sem levar em consideração possíveis efeitos relativísticos e de spin das partículas envolvidas. A forma mais simples de escrever o coeficiente de transmissão, nesse caso, é:
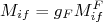 (25)
(25)sendo
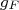 uma constante que representa a intensidade do acoplamento devido ao potencial de interação. O termo
uma constante que representa a intensidade do acoplamento devido ao potencial de interação. O termo 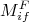 é tal que:
é tal que:
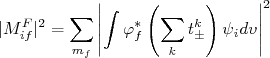 (26)
(26)A somatória em
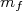 , projeção de momento angular total do núcleo final, vem da degenerescência do núcleo final nesse número quântico. A somatória em
, projeção de momento angular total do núcleo final, vem da degenerescência do núcleo final nesse número quântico. A somatória em 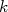 , no interior da integral. vem do fato da interação fraca poder ocorrer em todos os
, no interior da integral. vem do fato da interação fraca poder ocorrer em todos os 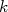 nucleons do núcleo inicial. Essa interação é representada por operadores de isospin,
nucleons do núcleo inicial. Essa interação é representada por operadores de isospin, 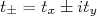 . Como sabemos, esses operadores satisfazem a algebra de momento angular de tal forma a, aplicados em um estado de isospin
. Como sabemos, esses operadores satisfazem a algebra de momento angular de tal forma a, aplicados em um estado de isospin 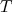 e projeção
e projeção  , aumentarem ou diminuem a projeção da componente z do isospin, satisfazendo as relações:
, aumentarem ou diminuem a projeção da componente z do isospin, satisfazendo as relações:
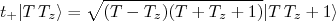 (27)
(27)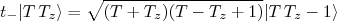 (28)
(28)O efeito prático desses operadores é de transformar um nêutron em próton ou vice-versa. Como discutimos anteriormente, o proton pode ser descrito como um estado
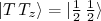 enquanto um nêutron pode ser descrito por
enquanto um nêutron pode ser descrito por 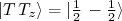 . Desse modo, temos:
. Desse modo, temos:
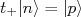 (29)
(29)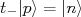 (30)
(30)Na prática, a somatória em
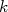 em (26), segundo o modelo de camadas, se reduz a poucos termos, dependendo do preenchimento dos níveis de energia, atuando, geralmente, apenas nos nucleons de valência. Isso porque, a transformação de um nucleon em um nível cheio para o outro nucleon correspondente não é permitida pelo princípio de exclusão de Pauli. Em alguns decaimentos, como o
em (26), segundo o modelo de camadas, se reduz a poucos termos, dependendo do preenchimento dos níveis de energia, atuando, geralmente, apenas nos nucleons de valência. Isso porque, a transformação de um nucleon em um nível cheio para o outro nucleon correspondente não é permitida pelo princípio de exclusão de Pauli. Em alguns decaimentos, como o 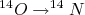 (ver exercício), esse elemento de matriz pode ser calculado facilmente. Nesse caso, conhecendo-se a meia vida do decaimento, pode-se determinar o valor da constante de acoplamento
(ver exercício), esse elemento de matriz pode ser calculado facilmente. Nesse caso, conhecendo-se a meia vida do decaimento, pode-se determinar o valor da constante de acoplamento 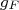 .
.
Substituindo (25) em (23) chegamos, finalmente, à:
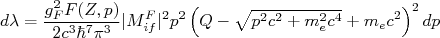 (31)
(31)A constante de decaimento
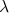 é obtida por integração de (31):
é obtida por integração de (31):
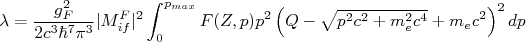 (32)
(32)Podemos definir a integral de Fermi,
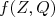 ou, como representada em alguns trabalhos,
ou, como representada em alguns trabalhos, 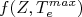 , como:
, como:
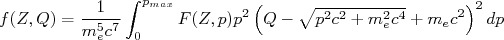 (33)
(33)As constantes em (33) deixam essa integral adimensional. Os valores da integral de Fermi são normalmente tabelados ou apresentados graficamente (ver figura 6).
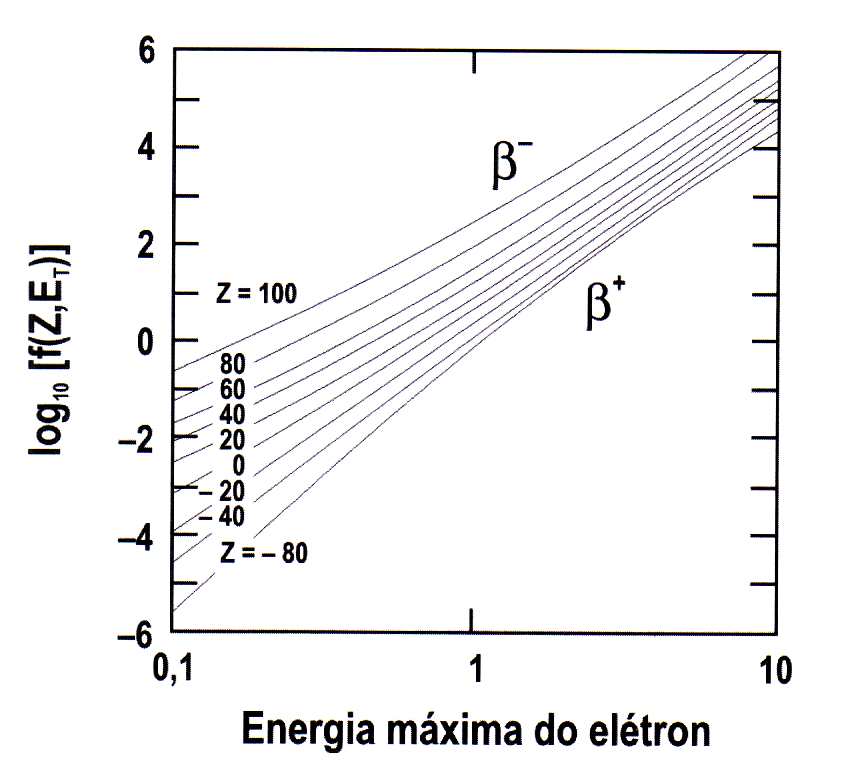
Desse modo, a constante de decaimento é escrita como:
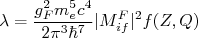 (34)
(34)Note que no modelo construído acima, consideramos apenas o termo de transição permitida para as funções de onda da partícula β e neutrino, bem como consideramos o neutrino uma partícula sem massa. Nesse modelo, também, efeitos interessantes, como violação de paridade, não são contemplados. A seguir vamos discutir esses fenômenos, que tornaram a física envolvida no decaimento β tão intrigante ao longo do século XX. Antes disso, porém, vamos introduzir duas representações para os resultados obtidos anteriormente de modo a facilitar consideravelmente a análise dos dados de decaimento β.
Gráfico de Kurie
O modelo descrito anteriormente possui algumas suposições. Duas importantes suposições são a hipótese da massa nula do neutrino (que discutiremos na próxima aula) e a adoção apenas do termo de transição permitida nas funções de onda da partícula β e neutrino. Dessas suposições, deduzimos a expressão para a constante de decaimento , que está relacionada à forma espectral para emissão de partículas β. De forma simplificada, o espectro de emissão de elétrons é dado por:
, que está relacionada à forma espectral para emissão de partículas β. De forma simplificada, o espectro de emissão de elétrons é dado por:
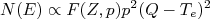 (35)
(35)A partir dessa relação podemos construir um gráfico de
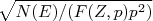 em função de
em função de  . Esse gráfico é chamado de gráfico de Kurie e é muito útil para identificar fenômenos não previstos pela teoria de Fermi descrito acima. Caso as suposições utilizadas na construção dessa teoria sejam válidas, espera-se uma reta para esse gráfico. Um exemplo é mostrado na figura 7, para o decaimento β do neutron, no qual esse gráfico apresenta um comportamento bem linear em grande parte da figura. Um outro exemplo é mostrado na figura 8, para o decaimento do 66Ga. Note que, também nesse caso, há uma dependência linear para uma porção significativa dos dados.
. Esse gráfico é chamado de gráfico de Kurie e é muito útil para identificar fenômenos não previstos pela teoria de Fermi descrito acima. Caso as suposições utilizadas na construção dessa teoria sejam válidas, espera-se uma reta para esse gráfico. Um exemplo é mostrado na figura 7, para o decaimento β do neutron, no qual esse gráfico apresenta um comportamento bem linear em grande parte da figura. Um outro exemplo é mostrado na figura 8, para o decaimento do 66Ga. Note que, também nesse caso, há uma dependência linear para uma porção significativa dos dados.
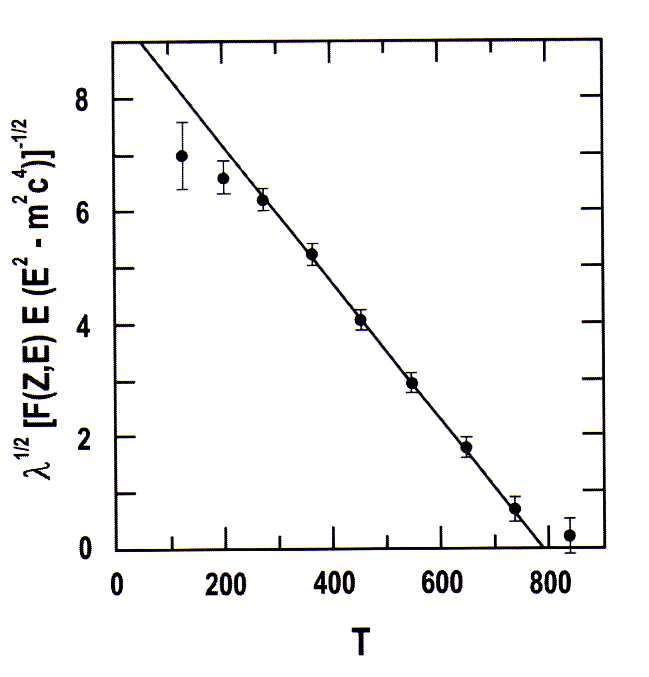
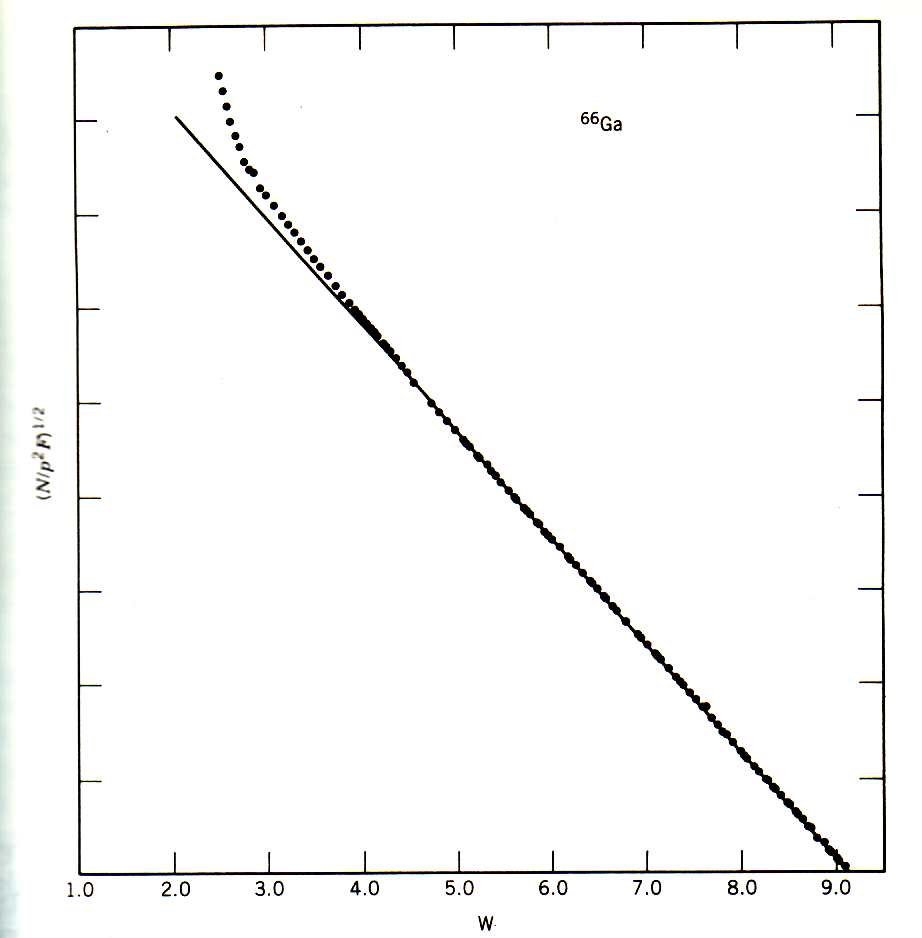
Desvios em relação a uma reta indicam a presença de fenômenos não considerados na teoria proposta. No caso da figura 8, por exemplo, os desvios em baixos momentos são atribuídos ao espalhamento das partículas β dentro da fonte radioativa, antes de atingirem o detector o que não seria, nesse caso específico, uma limitação da teoria proposta e sim uma limitação experimental. Contudo, pode-se observar também desvios significativos que indicariam fenômenos não considerados no desenvolvimento teórico. Por exemplo, na figura 8 mostramos um gráfico de Kurie que não apresenta nenhuma região linear. Esse gráfico corresponde ao decaimento β- do 91Y. Essa forma não linear é resultante da predominância de um decaimento proibido. No caso de decaimentos proibidos, o elemento de matriz em (19), tomando as expansões em (10) e (11), possuem uma dependência extra nos momentos do elétron e neutrino. Por exemplo, o primeiro termo proibido possui a dependência
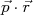 , gerando basicamente um termo extra de
, gerando basicamente um termo extra de 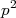 na forma espectral.
na forma espectral.
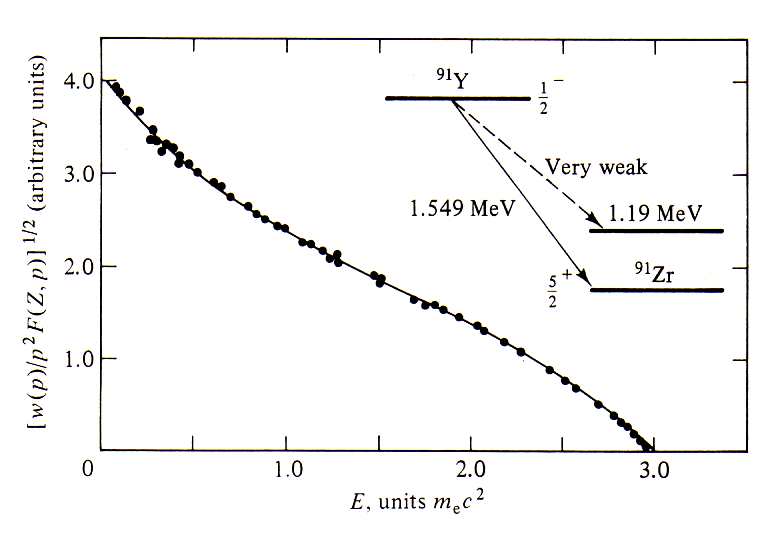
Pode-se também utilizar o gráfico de Kurie para investigar a possibilidade não nula para a massa do neutrino. Nesse caso, a energia cinética máxima das partículas β não seria mais o valor-Q considerado, pois essa foi calculada supondo a massa do neutrino nula. Nesse caso, a parte final do gráfico de Kurie seria deslocada e esse deslocamento seria uma medida da massa do neutrino. Contudo, essa é uma medida muito difícil de ser feita por conta da elevada precisão requerida. Voltaremos a esse assunto na próxima aula.
A meia-vida comparativa, ou fτ
A constante de decaimento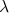 , como mostrada em (34), depende fortemente da integral de Fermi. A fim de comparar decaimentos β de diferentes núcleos, define-se uma quantidade denominada meia-vida comparativa, representada for
, como mostrada em (34), depende fortemente da integral de Fermi. A fim de comparar decaimentos β de diferentes núcleos, define-se uma quantidade denominada meia-vida comparativa, representada for 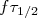 , ou simplesmente
, ou simplesmente 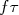 , dada pelo produto da meia-vida do decaimento e a integral de Fermi para esse mesmo decaimento. A partir da definição de meia-vida e de (34) pode-se chegar facilmente à:
, dada pelo produto da meia-vida do decaimento e a integral de Fermi para esse mesmo decaimento. A partir da definição de meia-vida e de (34) pode-se chegar facilmente à:
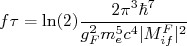 (36)
(36)O interessante de (36) é que o valor
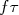 depende apenas do elemento de matriz para o decaimento e da constante
depende apenas do elemento de matriz para o decaimento e da constante 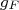 , que determina a intensidade da interação fraca sendo, portanto, útil para investigar diferenças entre decaimentos de núcleos similares.
, que determina a intensidade da interação fraca sendo, portanto, útil para investigar diferenças entre decaimentos de núcleos similares.
Uma situação interessante ocorre para transições
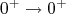 . Nessas transições (ver exercício), o elemento de matriz, segundo a teoria proposta, pode ser facilmente calculado, resultando em
. Nessas transições (ver exercício), o elemento de matriz, segundo a teoria proposta, pode ser facilmente calculado, resultando em 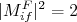 . Nesse caso, espera-se que transições desse tipo possuam o mesmo
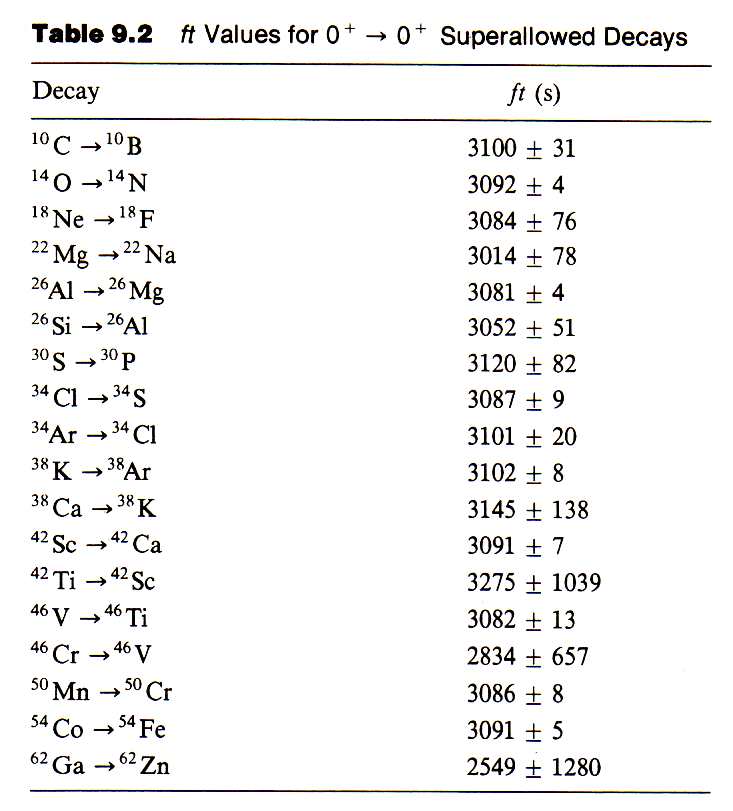
. Nesse caso, espera-se que transições desse tipo possuam o mesmo 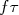 . Na figura 10, apresentamos uma tabela com as constantes
. Na figura 10, apresentamos uma tabela com as constantes 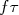 de vários decaimentos com transição
de vários decaimentos com transição 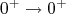 , cujos decaimentos sejam predominantemente os permitidos. Note a similaridade entre os valores de
, cujos decaimentos sejam predominantemente os permitidos. Note a similaridade entre os valores de 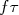 . A partir desses valores, podemos extrair a intensidade da constante de interação fraca
. A partir desses valores, podemos extrair a intensidade da constante de interação fraca 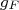 , obtendo:
, obtendo:
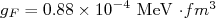 (37)
(37)
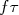 para decaimentos com transição
para decaimentos com transição 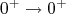
Apesar da teoria de Fermi explicar bem as propriedades observadas no decaimento β tais como constantes de decaimento e formas espectrais, ela não explica vários detalhes sutis do decaimento β, como violação de paridade. Teorias mais modernas, que incluem troca de partículas, como os bósons
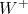 e
e 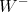 são mais adequadas nesse caso. Além disso, com a introdução do neutrino, vários fenômenos intrigantes foram observados nas décadas que se seguiram, criando uma nova área de pesquisa em física: a física de neutrinos. Esses serão os assuntos da próxima aula.
são mais adequadas nesse caso. Além disso, com a introdução do neutrino, vários fenômenos intrigantes foram observados nas décadas que se seguiram, criando uma nova área de pesquisa em física: a física de neutrinos. Esses serão os assuntos da próxima aula.
Exercícios
- Obtenha uma expressão para o espectro de energia de elétrons considerando a massa do neutrino diferente de zero. Faça o gráfico desse espectro para massas do neutrino de 1, 10 e 100 eV/c2. Compare os resultados.
- Mostre que, no decaimento β+ do 14O (0+) para o 14N (0+) temos que
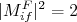 .
.
- Supondo que a massa do elétron seja pequena se comparada à energia do decaimento β, ache uma forma simplificada para o espectro de energia dos elétrons emitidos. Mostre que, nesse caso, o valor médio de energia é Q/2.
- Neutrons decaem em prótons com vida-média de 889 segundos. Conhecendo a diferença de massas entre pótons e neutrons e usando o valor de
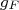 obtido anteriormente, obtenha
obtido anteriormente, obtenha 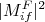 para essa transição.
para essa transição.
- A captura eletrônica pode ser calculada de forma similar ao realizado para o decaimento β. Mostre que a constante de decaimento para a captura eletrônica, em relação à obtida para o decaimento β+ pode ser dada por:
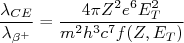
DICA: A função de onda inicial do sistema para a captura eletrônica inclui um elétron e um núcleo, enquanto a função de onda final, apenas o núcleo residual e neutrino. No caso da função de onda inicial, suponha que o elétron esteja na camada K do núcleo (lembre-se da energia de ligação desse elétron) e tome o seu limite para valores muito pequenos de raio, pois o elétron deve estar no interior do núcleo para ocorrer a captura eletrônica.
Leitura recomendada
- Paper de E. Fermi sobre decaimento β (tradução do artigo original em alemão), Versuch einer Theorie der β-Strahlen, E. Fermi, Zeitschrift für Physik A, 88 (1934) 161-177. Tradução: Fermi's Theory of Beta Decay, F. L. Wilson, American Journal of Physics, 36 (1968) 1150-1160.
- Discussão sobre função de Fermi, P Venkataramaiah, K Gopala, A Basavaraju, S S Suryanarayana and H Sanjeeviah, J. Phys. G: Nucl. Phys. 11 (1985) 359-364
- Introdução à Física Nuclear, H. Schechter e C. A. Bertulani, capítulo 7.
- Introductory Nuclear Physics, K. S. Krane, capítulo 9.
- Introduction to Nuclear and Particle Physics, A. Das e T. Ferbel, capítulo IV.




Oi Suaide,
No exercício 2, o elemento de Matriz do decaimento 140 -> 14N só será diferente de zero se o próton e o neutron da última camada do nitrogenio estiverem na configuração tripleto de isospin. Como saber que de fato é essa a configuração deles? Porque, por exemplo, no deuteron eles se encontram no estado singleto de isospin…