Momentos eletromagnéticos
Notas de aula são propriedade intelectual. Sendo assim, qualquer uso, no todo ou em parte, deve ter a origem referenciada apropriadamente, após autorização de seu autor.
O texto a seguir corresponde à anotações parciais de aula. Não é um texto em forma final, completo e totalmente revisado. Nesse caso, esse texto não tem como objetivo substituir livros sobre o assunto. Assim, esse texto deve ser entendido apenas como um guia de estudo para o aluno acompanhar a disciplina.
Nesse ponto já investigamos características importantes do núcleo, como raio, massa e propriedades relacionadas a momentos angulares. Muitas propriedades das interações fortes podem ser extraídas qualitativamente dessas características, como a saturação da força nuclear (curto alcance), a incompressibilidade do núcleo em condições normais, o balanço entre interações eletromagnéticas e fortes, estabilidade, etc. Muitos dos métodos empregados para inferir essas características, contudo, usam pouco de processos envolvendo, de fato, a interação forte. Note, por exemplo, que medidas de raios nucleares usam basicamente interações eletromagnéticas enquanto, grande parte da questão de estabilidade nuclear está diretamente relacionada à estabilidade β (interação fraca). Nesse tópico nós continuaremos a explorar algumas características nucleares novamente utilizando de propriedades eletromagnéticas do núcleo. Vamos estudar os multipolos eletromagnéticos.
Medidas de raios nucleares por espalhamento de elétrons medem a distribuição média de carga em um núcleo. Em primeira aproximação podemos tratar os núcleos como esféricos, de acordo com os resultados de espalhamento de elétrons. Contudo, o núcleo não é perfeitamente esférico e pequenos desvios provocam pequenas alterações no potencial coulombiano gerado por esses núcleos, que podem ser medidos e relacionadas a sua forma. Esses são os momentos eletrostáticos nucleares.
Por outro lado, os nucleons não são estáticos dentro do núcleo. Esse movimento resulta em correntes internas ao núcleo, resultando em campos magnéticos. Esses campos magnéticos estão, então relacionados à dinâmica dos nucleons no núcleo e, consequentemente, à sua estrutura. Essas propriedades dinâmicas são quantificadas através dos momentos magnéticos nucleares e fornecem informações importantes sobre momentos angulares e spin nucleares.
Momentos elétricos do núcleo
O potencial elétrico da distribuição de carga nuclear em um ponto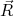 pode ser escrito como:
pode ser escrito como:
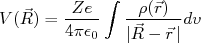 (1)
(1)Com
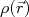 a distribuição de carga no núcleo normalizada, ou seja:
a distribuição de carga no núcleo normalizada, ou seja:
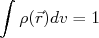 (2)
(2)Podemos escrever que:
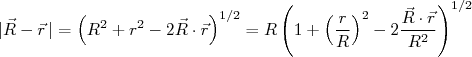
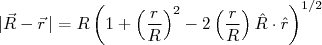 (3)
(3)Substituindo (3) em (1), temos:
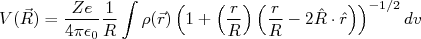 (4)
(4)Como
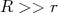 , podemos fazer uma expansão em Série de Taylor do termo de raiz quadrada da expressão (4), utilizando:
, podemos fazer uma expansão em Série de Taylor do termo de raiz quadrada da expressão (4), utilizando:
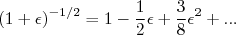 (5)
(5)com:
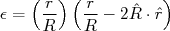 (6)
(6)Substituindo (5) e (6) em (4) e mantendo apenas os termos até a potência
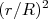 , temos:
, temos:
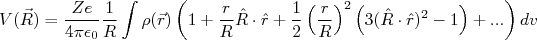 (7)
(7)A expressão (7) pode ser escrita como uma séries de termos, de acordo com a potência de
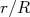 na forma:
na forma:
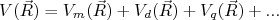 (8)
(8)com chamado termo de monopolo elétrico,
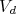 , termo de dipolo elétrico e
, termo de quadrupolo elétrico. Vamos olhar cada um desses termos separadamente.
, termo de dipolo elétrico e
, termo de quadrupolo elétrico. Vamos olhar cada um desses termos separadamente.
O termo de monopolo possui solução trivial:
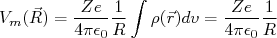 (9)
(9)e corresponde ao potencial gerado pelo núcleo considerando o mesmo como sendo perfeitamente esférico. Esse termo é dominante em relação aos outros e, em primeira aproximação foi utilizado para extrair propriedades nucleares importantes, como tamanho médio do núcleo.
O segundo termo, de dipolo elétrico, vale:
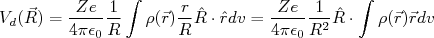 (10)
(10)define-se o momento de dipolo elétrico de uma distribuição de carga como sendo (note que a carga total do núcleo foi excluída dessa definição. Isso é bastante comum em física nuclear):
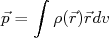 (11)
(11)Assim, a equação (10) torna-se:
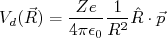 (12)
(12)Pelo fato do núcleo ser um sistema quântico, devemos exprimir a distribuição de carga do núcleo em termos da sua função de onda, ou seja:
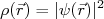 . Essa substituição gera uma consequência importante sobre o momento de dipolo elétrico do núcleo. Como vimos, o núcleo atômico possui estados sempre de paridade bem definida. Por conta disso,
. Essa substituição gera uma consequência importante sobre o momento de dipolo elétrico do núcleo. Como vimos, o núcleo atômico possui estados sempre de paridade bem definida. Por conta disso, 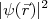 será sempre par. Da expressão (11), podemos ver, então, que o integrando será sempre uma função impar, resultando que a integral, no espaço, será sempre nula, tendo como consequência que o momento de dipolo elétrico de um núcleo é sempre nulo. Isso vai ocorrer também para todos os termos ímpares de expansão multipolar elétrica do núcleo. Como consequência, podemos definir um plano de simetria para a distribuição de carga de um núcleo, o que simplifica consideravelmente o entendimento sobre a sua forma.
será sempre par. Da expressão (11), podemos ver, então, que o integrando será sempre uma função impar, resultando que a integral, no espaço, será sempre nula, tendo como consequência que o momento de dipolo elétrico de um núcleo é sempre nulo. Isso vai ocorrer também para todos os termos ímpares de expansão multipolar elétrica do núcleo. Como consequência, podemos definir um plano de simetria para a distribuição de carga de um núcleo, o que simplifica consideravelmente o entendimento sobre a sua forma.
O potencial de quadrupolo elétrico é:
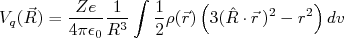 (13)
(13)Podemos simplificar a expressão acima tomando:
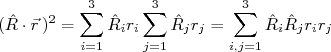 (14)
(14)e
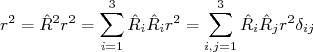 (15)
(15)Substituindo (14) e (15) em (13), e tirando a somatória para fora da integral, temos:
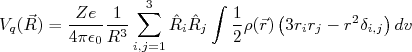 (16)
(16)Podemos definir o tensor momento de quadrupolo elétrico como sendo:
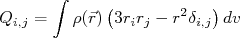 (17)
(17)De modo que:
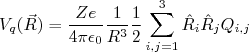 (18)
(18)Pode-se notar, a partir de (17) que as componentes do momento de quadrupolo possuem unidade de área. Costuma-se expressar esses momentos em unidades de barn (1 barn = 10-28 m2). O tensor momento de quadrupolo possui, a princípio, nove componentes. Contudo, é fácil ver, por razões de simetria que
 , reduzindo o tensor a apenas 6 componentes independentes.
, reduzindo o tensor a apenas 6 componentes independentes.
No caso nuclear podemos utilizar outros critérios de simetria para reduzir ainda mais o número de componentes desse tensor. Vamos considerar que a forma nuclear, por simplicidade, é um elipsóide de revolução em torno de um eixo-z qualquer. Nesse caso, pode-se mostrar que o tensor momento de quadrupolo possui apenas uma componente não nula, dada por:
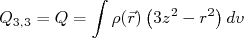 (19)
(19)Nessa situação, o potencial de quadrupolo se reduz à:
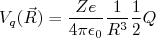 (20)
(20)A equação (19) fornece informações relevantes à forma da distribuição de carga. Se, o termo da integral que depende de
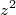 prevalece sobre o termo
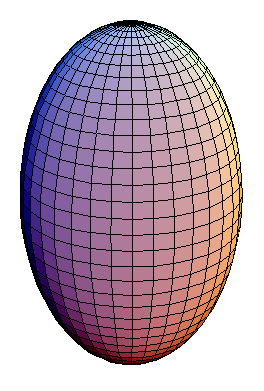
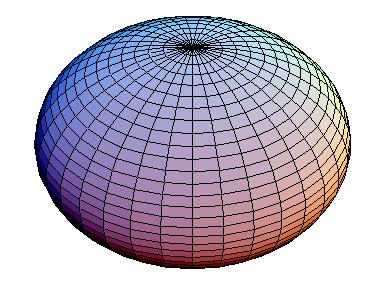
prevalece sobre o termo 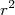 , o momento de quadrupolo é maior que zero. Nesse caso, a distribuição de carga está mais concentrada ao longo do eixo-z. Chamamos essa distribuição de prolata. Se o contrário ocorre, a distribuição de carga está mais concentrada ao longo do plano de simetria. O sistema é mais achatado, ou oblato. A figuras 1 e 2 mostram essas distribuições. Se o núcleo for esfericamente simétrico,
, o momento de quadrupolo é maior que zero. Nesse caso, a distribuição de carga está mais concentrada ao longo do eixo-z. Chamamos essa distribuição de prolata. Se o contrário ocorre, a distribuição de carga está mais concentrada ao longo do plano de simetria. O sistema é mais achatado, ou oblato. A figuras 1 e 2 mostram essas distribuições. Se o núcleo for esfericamente simétrico, 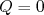 .
.
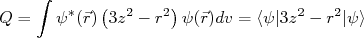 (21)
(21)Calcular o momento de quadrupolo elétrico de um núcleo não é uma tarefa simples pois a função de onda que descreve o seu estado quântico pode ser bastante complexa. Podemos, contudo, tentar simplificar esse cálculo através de algumas aproximações. Para um núcleo par-par, o momento angular de seu estado fundamental é nulo. Nesse caso, pode-se inferir que, por conta desse estado, a distribuição de carga seja esfericamente simétrica e o momento de quadrupolo seja muito próximo de zero. Assim, para um núcleo ímpar ou ímpar-ímpar o momento de quadrupolo pode ser estimado considerando os nucleons de valência, ou seja, aqueles que não estão emparelhados. No caso de nêutrons como nucleons de valência, esperamos que o momento de quadrupolo desse nucleon também seja nulo, por conta da carga elétrica nula do nêutron. Resta o caso no qual temos um núcleo com Z ímpar. Nesse caso, calcularemos o momento de quadrupolo elétrico como sendo aquele para o próton de valência. Para um próton em um estado de momento angular
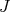 , há
, há 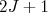 possíveis auto-estados. Nesse caso define-se o momento de quadrupolo como aquele calculado no auto-estado de maior projeção
possíveis auto-estados. Nesse caso define-se o momento de quadrupolo como aquele calculado no auto-estado de maior projeção 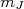 para o momento angular total. Assim, de (21) escrevemos:
para o momento angular total. Assim, de (21) escrevemos:
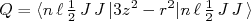 (22)
(22)O segundo
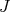 equilave ao valor de
equilave ao valor de 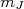 . Para um núcleo em um estado de momento angular orbital
. Para um núcleo em um estado de momento angular orbital 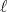 e spin 1/2, o momento angular total pode assumir dois valores distintos,
e spin 1/2, o momento angular total pode assumir dois valores distintos, 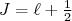 ou
ou 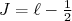 . No primeiro caso, há apenas uma possibilidade de compor o momento angular orbital com spin (
. No primeiro caso, há apenas uma possibilidade de compor o momento angular orbital com spin (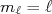 e
e 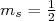 ). Assim, podemos escrever a função de onda desse estado como sendo:
). Assim, podemos escrever a função de onda desse estado como sendo:
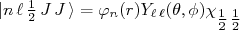 (23)
(23)A componente de spin da função de onda
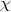 não atua no operador momento de quadrupolo, pois o mesmo só depende de coordenadas espaciais. Como essa componente é normalizada, o valor esperado de momento de quadrupolo elétrico se restringe à:
não atua no operador momento de quadrupolo, pois o mesmo só depende de coordenadas espaciais. Como essa componente é normalizada, o valor esperado de momento de quadrupolo elétrico se restringe à:
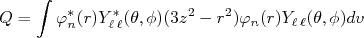 (24)
(24)reescrevendo
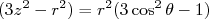 podemos decompor a integral acima na parte radial e angular. A parte radial resulta no valor esperado para raio quadrático médio e assim:
podemos decompor a integral acima na parte radial e angular. A parte radial resulta no valor esperado para raio quadrático médio e assim:
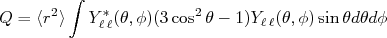 (25)
(25)A integral em (25) pode ser resolvida (exercício) resultando em:
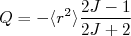 (26)
(26)Para o segundo caso de momento angular,
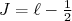 , há duas possibilidades de acoplamento,
, há duas possibilidades de acoplamento, 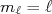 e
e  OU
OU 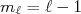 e
e 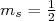 . Nesse caso, a função de onda é a composição desses dois estados, cada um com peso relativo dado pelo coeficiente de Clebsch-Gordan correspondente, ou seja:
. Nesse caso, a função de onda é a composição desses dois estados, cada um com peso relativo dado pelo coeficiente de Clebsch-Gordan correspondente, ou seja:
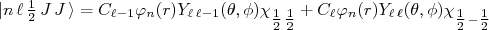 (27)
(27)Da mesma forma que no caso anterior, o resultado obtido para o momento de quadrupolo resulta na equação (26) (exercício).
Vamos então comparar a previsão desse modelo simples com resultados experimentais para núcleos diversos. Primeiramente vale notar que os valores de momento de quadrupolo elétrico são sempre negativos. Isso vem da escolha realizada para
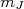 ser máxima. Nesse caso, alinhamos o momento angular total no eixo-z, resultando em um estado localizado principalmente no plano x-y. As figuras 3 e 4 mostram informações sobre momentos de quadrupolo elétrico medidos e calculados com esse modelo. Na figura 3 vemos que em alguns casos reproduzimos o sinal do momento de quadrupolo. Contudo a magnitude está incorreta. No caso do 175Lu, além do sinal estar errado, a magnitude do momento de quadrupolo experimental é muito maior que a calculada. Essa é uma característica comum em elementos Terra Rara, que possuem estados coletivos de elevada deformação e, nesse caso, o modelo de nucleon de valência não dá conta de reproduzir toda essa deformação.
ser máxima. Nesse caso, alinhamos o momento angular total no eixo-z, resultando em um estado localizado principalmente no plano x-y. As figuras 3 e 4 mostram informações sobre momentos de quadrupolo elétrico medidos e calculados com esse modelo. Na figura 3 vemos que em alguns casos reproduzimos o sinal do momento de quadrupolo. Contudo a magnitude está incorreta. No caso do 175Lu, além do sinal estar errado, a magnitude do momento de quadrupolo experimental é muito maior que a calculada. Essa é uma característica comum em elementos Terra Rara, que possuem estados coletivos de elevada deformação e, nesse caso, o modelo de nucleon de valência não dá conta de reproduzir toda essa deformação.
Há ainda alguns casos interessantes, na figura 3, para núcleos com N ímpar. Esperávamos que o momento de quadrupolo desses núcleos fosse nulo, como o nosso modelo assume. Os momentos de quadrupolo desses núcleos não são nulos, apesar de pequenos. Isso pode ser explicado pelo fato do nucleon de valência interagir com o caroço par-par do núcleo. Essa interação pode causar uma pequena polarização desse caroço, gerando o momento de quadrupolo observado.
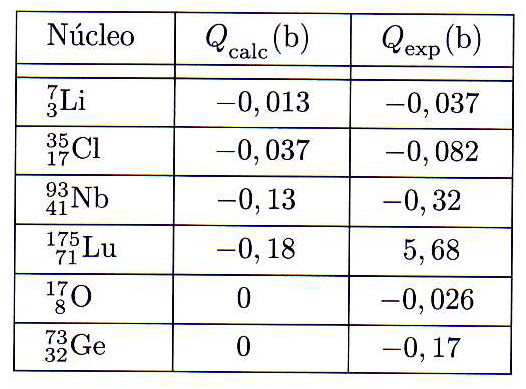
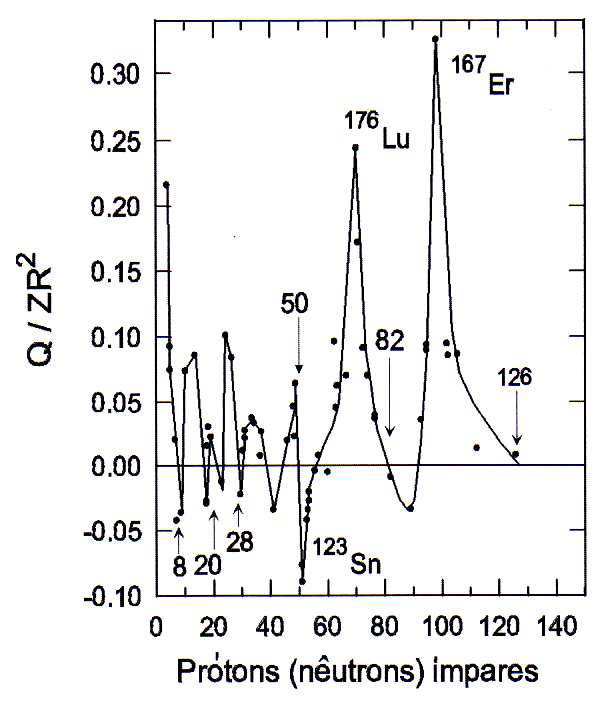
Na figura 4 vemos valores de momentos de quadrupolo em função de Z (ou N) para núcleos ímpares. Note que há vários núcleos com momentos positivos e negativos. A transição entre valores positivos e negativos ocorre periodicamente em valores de Z (ou N) bem determinados. Esses valores irão surgir novamente quando discutirmos números mágicos em modelo de camadas, pois correspondem a valores nos quais se preenche totalmente uma camada nuclear, o que tem implicações diretas no momento de quadrupolo elétrico nuclear.
Momentos magnéticos do núcleo
Um estado nuclear qualquer com vários nucleons é formado da composição dos mesmos em diferentes estados de momento angular e spin. Por conta disso há um arranjo complexo de correntes elétricas no núcleo. É natural pensar que essas correntes elétricas geram campos magnéticos. A medida desses campos magnéticos fornece dados para compreender melhor a estrutura e distribuição de partículas no núcleo. Em um sistema no qual as correntes estão bem localizadas, como no núcleo atômico, é possível descrever o campo magnético como sendo o rotacional de um potencial vetorial. Esse potencial vetor, nessa situação, pode ser escrito como: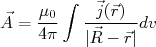 (28)
(28)Da mesma forma que fizemos com o potencial eletrostático nuclear, sabendo que
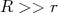 podemos expandir (28) em multipolos magnéticos. Realizando a mesma expansão anterior, temos:
podemos expandir (28) em multipolos magnéticos. Realizando a mesma expansão anterior, temos:
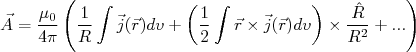 (29)
(29)O primeiro termo da expansão, denominado termo de monopolo magnético é nulo. O segundo termo é chamado termo de dipolo magnético. Considerando apenas esse termo, temos:
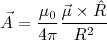 (30)
(30)onde
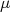 é denominado de momento de dipolo magnético, definido como:
é denominado de momento de dipolo magnético, definido como:
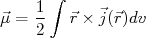 (31)
(31)Para uma espira circular de raio
 e corrente
e corrente 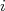 , o momento magnético é tal que
, o momento magnético é tal que 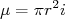 . Se essa corrente for devida a uma única partícula carregada (por exemplo, um elétron), circulando com velocidade
. Se essa corrente for devida a uma única partícula carregada (por exemplo, um elétron), circulando com velocidade  , podemos escrever:
, podemos escrever:
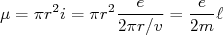 (32)
(32)onde
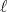 é o módulo do momento angular dessa partícula. Pode-se analogamente definir o vetor momento de dipolo magnético em mecânica quântica como sendo:
é o módulo do momento angular dessa partícula. Pode-se analogamente definir o vetor momento de dipolo magnético em mecânica quântica como sendo:
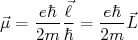 (33)
(33)Daqui para frente vamos nos referir aos vetores
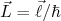 e
e 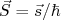 . A grandeza
. A grandeza 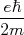 é chamada de magneton. Para um elétron temos que essa grandeza vale
é chamada de magneton. Para um elétron temos que essa grandeza vale 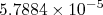 eV/T. Costuma-se chamá-la de magneton de Bohr e usar
eV/T. Costuma-se chamá-la de magneton de Bohr e usar 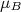 para representá-la. No caso nuclear, usando a massa do próton, temos o magneton nuclear, que vale
para representá-la. No caso nuclear, usando a massa do próton, temos o magneton nuclear, que vale 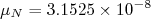 eV/T. Nesse caso é mais conveniente escrever (33) como:
eV/T. Nesse caso é mais conveniente escrever (33) como:
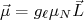 (34)
(34)onde
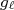 é um fator numérico associado ao momento angular e tipo de partícula e vale 1 para o próton e 0 para o nêutron, que não possui carga.
é um fator numérico associado ao momento angular e tipo de partícula e vale 1 para o próton e 0 para o nêutron, que não possui carga.
Observa-se que, mesmo estando em um estado de momento angular orbital nulo, nucleons possuem momento de dipolo magnético. Isso é devido ao seu spin. Nesse caso, adiciona-se uma componente à (34), de forma análoga, devido ao spin do nucleon, tornando o seu momento de dipolo:
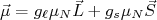 (35)
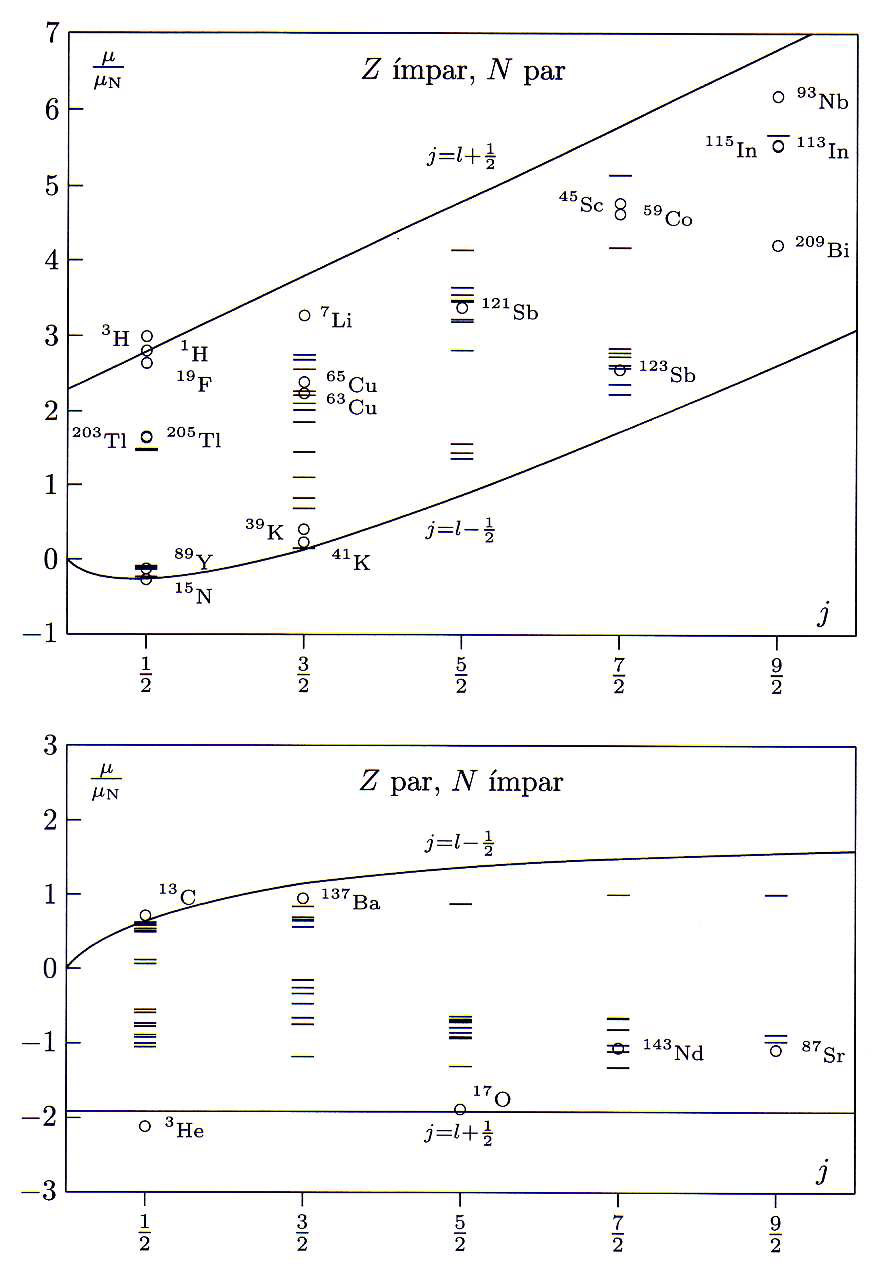
(35)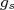 é conhecido como fator de spin e pode ser obtido a partir da equação de Dirac. Para uma partícula sem estrutura e spin 1/2, espera-se que
é conhecido como fator de spin e pode ser obtido a partir da equação de Dirac. Para uma partícula sem estrutura e spin 1/2, espera-se que 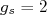 . Obtém-se experimentalmente para o elétron
. Obtém-se experimentalmente para o elétron 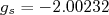 . O sinal negativo é devido à carga do elétron. Os valores experimentais obtidos para o próton e neutron são, respectivamente (Krane):
. O sinal negativo é devido à carga do elétron. Os valores experimentais obtidos para o próton e neutron são, respectivamente (Krane): 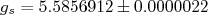 e
e 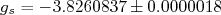 . O fato desse valor para o próton não ser compatível com 2 e o valor para o neutron não ser nulo é um forte indício que essas partículas não são pontuais, possuindo, portanto, estrutura interna. Note que a diferença
. O fato desse valor para o próton não ser compatível com 2 e o valor para o neutron não ser nulo é um forte indício que essas partículas não são pontuais, possuindo, portanto, estrutura interna. Note que a diferença 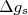 em relação ao valor esperado, em ambos os casos, é aproximadamente a mesma (~3.6) com sinal trocado. Essa diferença pode ser atribuída à núvem mesônica (píons) que envolve esses nucleons. No caso do próton essa núvem é composta basicamente por pions neutrons e positivos (quando da dissociação temporária do próton em neutron + pion) enquanto para o nêutron é composta de píons neutros e negativos (quando da da dissociação temporária do nêutron em próton + pion). As cargas opostas desses píons gera essa diferença de sinal. Note que essa é uma explicação por demais qualitativa, uma vez que o estudo de momentos de dipolo magnéticos de nucleons ainda é objeto de intenso estudo.
em relação ao valor esperado, em ambos os casos, é aproximadamente a mesma (~3.6) com sinal trocado. Essa diferença pode ser atribuída à núvem mesônica (píons) que envolve esses nucleons. No caso do próton essa núvem é composta basicamente por pions neutrons e positivos (quando da dissociação temporária do próton em neutron + pion) enquanto para o nêutron é composta de píons neutros e negativos (quando da da dissociação temporária do nêutron em próton + pion). As cargas opostas desses píons gera essa diferença de sinal. Note que essa é uma explicação por demais qualitativa, uma vez que o estudo de momentos de dipolo magnéticos de nucleons ainda é objeto de intenso estudo.
Assim como no caso do momento de quadrupolo elétrico, podemos calcular o momento de dipolo elétrico de um núcleo atômico. A princípio, calcular o momento de dipolo magnético seria extremamente complexo, pois teríamos que somar a contribuição de cada nucleon. Contudo, observações indicam que os momentos de dipolo magnético de todos os núcleos par-par são nulos. Isso permite assumir que o momento de dipolo magnético de um núcleo ímpar é dado pelo momento de dipolo magnético do nucleon desemparelhado. Como as direções dos vetores
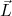 e
e 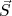 não são fixas, define-se, para fins práticos, o momento de dipolo como sendo a componente z de (35) calculada no valor máximo da projeção do momento angular total, ou seja,
não são fixas, define-se, para fins práticos, o momento de dipolo como sendo a componente z de (35) calculada no valor máximo da projeção do momento angular total, ou seja,  . Assim, para o nucleon desemparelhado no seu estado de momento angular, temos que:
. Assim, para o nucleon desemparelhado no seu estado de momento angular, temos que:
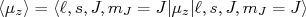 (36)
(36)Como as componentes z do vetor momento angular orbital e spin não são constantes do movimento, precisamos contornar esse pequeno problema. Podemos re-escrever (36) como:
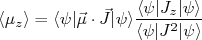
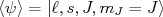
ou seja:
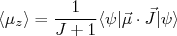 (37)
(37)Assim, substituindo (35) em (37) temos:
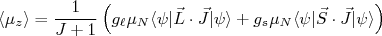 (38)
(38)Fazendo, por exemplo:
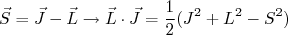 (39)
(39)de modo que (o mesmo pode ser feito para
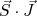 ):
):
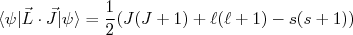 (40)
(40)Substituindo (40) (e o equivalente para o outro termo) em (38), podemos calcular o momento de dipolo magnético de nucleon desemparelhado.
No caso do nucleon desemparelhado, temos duas opções de acoplamento de momento angular orbital e spin em momento angular total:
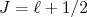 e
e 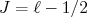 . Calculando (38) para essas duas opções temos, para
. Calculando (38) para essas duas opções temos, para 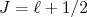 :
:
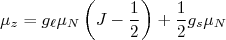 (41)
(41)e, para
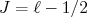 :
:
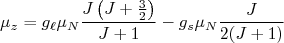 (42)
(42)As equações em (41) e (42) são chamadas Linhas de Schmidt e correspondem às duas possibilidades de momento de dipolo magnético para um determinado núcleo ímpar. Na figura 5 podemos ver essas linhas comparadas a valores experimentais para núcleos ímpares. Dessa figura podemos concluir:
- Os pontos experimentais se situam, na maioria dos casos, entre as duas linhas. Contudo, a incluinação da distribuição dos dados acompanha razoavelmente a inclinação das linhas. Como essa inclinação é dominada por
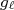 , podemos inferir que o valor de
, podemos inferir que o valor de 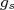 no núcleo não é igual àquele para núcleon livre. Como esse valor está relacionado com a núvem mesônica criada pelo nucleon, essa núvem deve ser modificada devido às interações entre nucleons e, portanto, espera-se, de fato, que
no núcleo não é igual àquele para núcleon livre. Como esse valor está relacionado com a núvem mesônica criada pelo nucleon, essa núvem deve ser modificada devido às interações entre nucleons e, portanto, espera-se, de fato, que 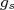 seja modificado.
seja modificado.
- outra forma de encarar esses dados que o modelo de nucleon de valência é uma simplificação exagerada. Se fosse o caso, núcleos nos quais o caroço correspondem a números mágicos (veremos isso mais a frente em modelo de camadas, guarde essa informação) estariam mais próximos das linhas de Schmidt. Isso não ocorre (círculos na figura 5). Isso sugere que, mesmo nesse caso, o nucleon desemparelhado pode gerar uma pequena polarização no caroço, como discutido do caso do momento de quadrupolo elétrico, e o mesmo passe a contrubuir para o momento de dipolo magnético.
Exercícios
- Mostre (26) a partir de (25).
- Usando (27), mostre (26).
- Mostre (30) a partir de (28).
- Mostre (41) e (42) a partir de (38).
- Supondo um núcleo na forma de um elipsóide de revolução, ou seja, usando a parametrização
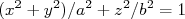 , deduza a expressão para o momento de quadrupolo elétrico desse núcleo em termos de
, deduza a expressão para o momento de quadrupolo elétrico desse núcleo em termos de  e
e 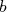 . Com base nos dados experimentais acima, calcule a razão
. Com base nos dados experimentais acima, calcule a razão 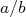 para o 175Lu.
para o 175Lu.
Leitura recomendada
- Introductory Nuclear Physics, K. S. Krane, capítulo 3.5.
- Introdução à Física Nuclear, H. Schechter e C. A. Bertulani, capítulos 1.7, 3.5 a 3.7.




No comments