Aproximação de Born
Notas de aula são propriedade intelectual. Sendo assim, qualquer uso, no todo ou em parte, deve ter a origem referenciada apropriadamente, após autorização de seu autor.
O texto a seguir corresponde à anotações parciais de aula. Não é um texto em forma final, completo e totalmente revisado. Nesse caso, esse texto não tem como objetivo substituir livros sobre o assunto. Assim, esse texto deve ser entendido apenas como um guia de estudo para o aluno acompanhar a disciplina.
Muitas das observações realizadas em Física Nuclear fazem uso de colisões entre partículas. Nesse caso, o estudo do espalhamento dessas partículas fornece as informações necessárias para o descobrimento das propriedades do núcleo atômico. É importante, nesse caso, um entendimento sólido acerca de teoria de espalhamento em Mecânica Quântica. Na medida do necessário tentarei discutir aspectos desse assunto. Nesse texto tratarei da aproximação de Born para espalhamento elástico. Darei mais atenção à dedução dessa aproximação e deixarei outros aspectos de lado. Contudo, imagino que esses aspectos não prejudicam a compreensão do que se segue.
Vamos tratar o espalhamento de uma partícula por outra. Algumas simplificações são necessárias para desenvolver este exercício nesse momento. Por exemplo, não trataremos de possíveis interações devido ao spin das partículas e também vamos lidar apenas com colisões elásticas, ou seja, desprezaremos possíveis estruturas internas que possam criar inelasticidade na colisão. Vamos assumir também que a interação entre as partículas possa ser descrita por um potencial que dependa apenas da distância entre elas. O tratamento correto exige que o desenvolvimento se dê no referencial do centro de massa do sistema. Nesse caso, pode-se descrever o processo de colisão no centro de massa como sendo o de uma partícula de massa efetiva
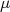 sendo espalhada por um potencial
sendo espalhada por um potencial 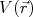 . Essa massa efetiva (também chamada de massa reduzida) vale:
. Essa massa efetiva (também chamada de massa reduzida) vale:
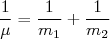 (1)
(1)No caso do espalhamento de elétrons por um núcleo pesado,
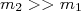 , de modo que
, de modo que  .
Como o potencial não depende do tempo, a evolução temporal da função de onda do sistema tem solução trivial. Desse modo, estudar o espalhamento resulta em estudar os auto-estados da Equação de Schrödinger independente do tempo, ou seja, obter as funções de onda
.
Como o potencial não depende do tempo, a evolução temporal da função de onda do sistema tem solução trivial. Desse modo, estudar o espalhamento resulta em estudar os auto-estados da Equação de Schrödinger independente do tempo, ou seja, obter as funções de onda 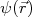 que satisfaçam:
que satisfaçam:
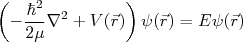 (2)
(2)Vamos assumir que o potencial de interação possua alcance finito, de forma que a partícula incidente, antes de interagir com o potencial, pode ser descrita como uma onda plana. Vamos assumir a direção de propagação do feixe de partículas como z, de modo a definir um vetor de onda
 . A energia da partícula, em termos do vetor de onda vale:
. A energia da partícula, em termos do vetor de onda vale:
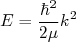 (3)
(3)Substituindo (3) em (2) e definindo
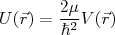 , podemos reduzir a expressão (2) à:
, podemos reduzir a expressão (2) à:
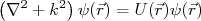 (4)
(4)Após a interação com o potencial a estrutura da função de onda é modificada. Em física nuclear, contudo, as medidas são realizadas assintoticamente, ou seja, em distâncias muito maiores que a região de interação. Nesse caso, a função de onda do sistema após interação com o potencial espalhador pode ser escrita como sendo a superposição de uma onda plana de iguais características que a onda incidente e uma onda espalhada em todas as direções. Essa onda espalhada possui a mesma energia que a onda incidente. Essa onda deve possuir uma dependência radial que cai com 1/r. Essa dependência assegura que o fluxo total de partículas espalhadas não depende do raio no qual se posiciona o detector. A amplitude da onda espalhada pode depender, contudo, de (θ, φ) por conta do potencial espalhador. Assim, podemos escrever que a função é composta pela onda incidente e uma componente espalhada, ou seja:
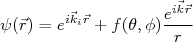 (5)
(5)A função
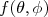 é denominada de amplitude de espalhamento e depende diretamente do potencial de interação.
é denominada de amplitude de espalhamento e depende diretamente do potencial de interação. 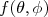 pode ser obtida experimentalmente a partir da medida de seção de choque diferencial. Para obter a seção de choque diferencial de espalhamento precisamos determinar o fluxo de partículas incidente e a taxa de partículas espalhadas, segundo a definição de seção de choque discutida em aula anterior. Em M.Q. define-se fluxo (ou corrente) como:
pode ser obtida experimentalmente a partir da medida de seção de choque diferencial. Para obter a seção de choque diferencial de espalhamento precisamos determinar o fluxo de partículas incidente e a taxa de partículas espalhadas, segundo a definição de seção de choque discutida em aula anterior. Em M.Q. define-se fluxo (ou corrente) como:
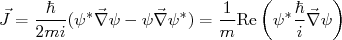 (6)
(6)O fluxo incidente pode ser calculado como:
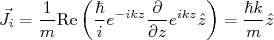 (7)
(7)O fluxo espalhado pode ser feito da mesma maneira que o incidente, considerando o termo de espalhamento da função de onda em (5). Note que, nesse caso, estamos negligenciando possíveis contribuições devido à interferência entre a onda incidente e espalhada. Isso pode ser feito considerando que estamos medindo seção de choque em ângulos de espalhamento não muito próximos de zero, o que é, em geral, verdadeiro. Dessa vez, contudo, é mais simples considerar o gradiente em coordenadas esféricas, ou seja:
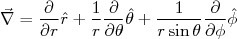 (8)
(8)Como estamos pensando na solução assintótica, ou seja, r muito grande, podemos assumir que os termos angulares no gradiente são muito pequenos, ou seja, o fluxo espalhado é puramente radial. Nesse caso, o fluxo espalhado pode ser dado por:
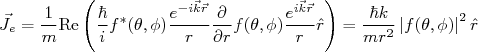 (9)
(9)A seção de choque é a razão entre o número de partículas espalhadas e o fluxo incidente, ou seja:
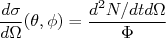 (10)
(10)Sendo
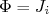 e:
e:
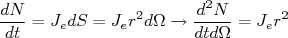 (11)
(11)Substituindo (7), (9) e (11) em (10), resulta em:
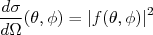 (12)
(12)Pode-se calcular a seção de choque a partir de
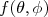 . Contudo, ainda precisamos relacionar
. Contudo, ainda precisamos relacionar 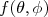 com o potencial de interação, pois é esse que contém informação acerca da interação entre as partículas envolvidas no processo de espalhamento. Há muitas técnicas e métodos para fazer essa associação.
com o potencial de interação, pois é esse que contém informação acerca da interação entre as partículas envolvidas no processo de espalhamento. Há muitas técnicas e métodos para fazer essa associação.
Vamos inferir uma solução para a equação (4) considerando o potencial e obter
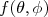 . Inicialmente, vamos supor que exista uma função
. Inicialmente, vamos supor que exista uma função  que satisfaça a seguinte equação:
que satisfaça a seguinte equação:
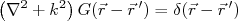 (13)
(13)Essa função é chamada de Função de Green para o operador
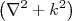 . Havendo essa função, a função de onda espalhada pelo potencial pode ser escrita como:
. Havendo essa função, a função de onda espalhada pelo potencial pode ser escrita como:
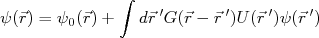 (14)
(14)Vamos verificar se (14) realmente é uma solução para (4). Para isso, substituimos (14) em (4). Obtemos:
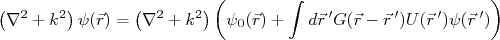
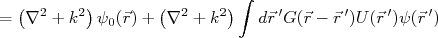
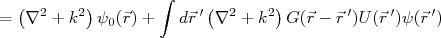
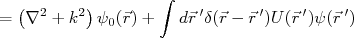
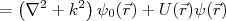 (15)
(15)A equação (15) se iguala à (4) se
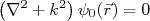 . Isso é verdade se
. Isso é verdade se 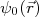 for uma onda plana com número de onda
for uma onda plana com número de onda 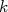 . A função
. A função 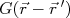 que satisfaz (13) vale (consulte o seu livro de FísMat favorito):
que satisfaz (13) vale (consulte o seu livro de FísMat favorito):
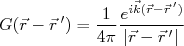 (16)
(16)Para obter a função de onda na expressão (14) precisamos conhecê-la previamente, pois a integral do lado direito da expressão depende da função de onda. Para contornar esse problema, vamos fazer uma expansão na expressão (14) conhecida como expansão de Born. Essa expansão consiste em alterar os índices
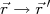 e
e 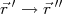 e substituir no lado direito de (14). Assim:
e substituir no lado direito de (14). Assim:
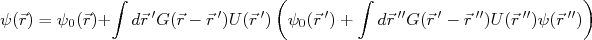
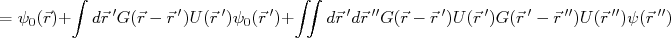 (17)
(17)Note que, nesse caso, a expansão "empurrou" a função de onda para um termo quadrático no potencial. Podemos fazer essa substituição sucessivamente indefinidamente. Supondo que o potencial de interação seja pequeno, de modo que o seu quadrado seja ainda menor, podemos tomar apenas o primeiro termo da expansão, desprezando os seguintes. Nesse caso, a expressão (17) resulta em:
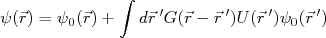 (18)
(18)Sabendo que
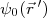 é uma onda plana e que
é uma onda plana e que 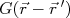 é dada por (16), podemos escrever que:
é dada por (16), podemos escrever que:
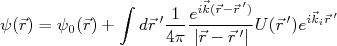 (19)
(19)No limite de
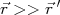 podemos escrever que:
podemos escrever que:
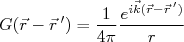 (20)
(20)de modo que:
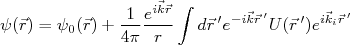 (21)
(21)Comparando (5) com (21), podemos, finalmente, escrever que:
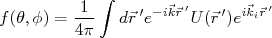 (22)
(22)Assim, a seção de choque diferencial de espalhamento, dada pela expressão (6), substituindo
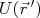 pelo equivalente para
pelo equivalente para 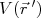 fica sendo:
fica sendo:
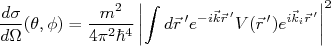 (23)
(23)A expressão (23) é a chamada Aproximação de Born para seção de choque de espalhamento. É muito comum a representação de (23) na notação de Dirac, na qual podemos substituir a integral por BraKet, ou seja:
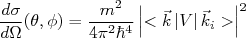 (24)
(24)Vamos olhar com calma a expressão (23) para seção de choque diferencial de espalhamento. Vamos definir o vetor de onda transferido transferido como sendo a diferença entre o vetor de onda final e inicial. Assim, fazendo
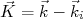 , temos que:
, temos que:
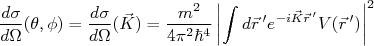 (25)
(25)Lembrando que a transformada de Fourier de uma função em um espaço tridimensional é dada por:
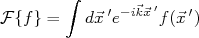 (26)
(26)é fácil notar que a seção de choque diferencial de espalhamento é proporcional ao módulo quadrático da transformada de Fourier do potencial de interação, ou seja:
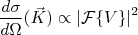 (27)
(27)A dependência da seção de choque com a transformada de Fourier do potencial, na aproximação de Born, permite, através de medidas experimentais, determinar o potencial de interação entre duas partículas interagentes. Essa técnica é muito utilizada em Física Nuclear para determinação de potenciais de interação.
Exercícios
- Demonstre (6) e (9).
- Desenvolva a expansão (equação 17) de Born até o termo de terceira ordem.
- Obtenha a seção de choque de espalhamento de Rutherford, utilizando a aproximação de Born, como na expressão (23).
Leitura recomendada
- Quantum Mechanics, Cohen-Tannoudji, capítulo VIII, volume 2.
- Tranformada de Fourier, http://en.wikipedia.org/wiki/Fourier_transform




No comments