O raio nuclear
Notas de aula são propriedade intelectual. Sendo assim, qualquer uso, no todo ou em parte, deve ter a origem referenciada apropriadamente, após autorização de seu autor.
O texto a seguir corresponde à anotações parciais de aula. Não é um texto em forma final, completo e totalmente revisado. Nesse caso, esse texto não tem como objetivo substituir livros sobre o assunto. Assim, esse texto deve ser entendido apenas como um guia de estudo para o aluno acompanhar a disciplina.
Uma grandeza fundamental para caracterização do núcleo atômico é o seu tamanho. No experimento original de Geiger e Marsden, Rutherford obteve que as dimensões típicas do núcleo seriam inferiores a 10-14 m. A descoberta que o núcleo atômico seria constituído basicamente por prótons (Rutherford, 1919, através da reação 42He + 147N -> 178O + p) e nêutrons (Chadwick, 1932, através da reação 42He + 94Be -> 126C + n) tornou importante o estudo da sua estrutura interna. Assim, a medida do seu tamanho, bem como a distribuição de matéria e carga no seu interior, se tornaram uma área importante de pesquisa em Física Nuclear.
São muitas as técnicas utilizadas para medir tamanho e distribuição de matéria no núcleo. Vamos discutir algumas delas a seguir, bem como suas peculiaridades e limitações. Antes de prosseguir, contudo, vamos construir uma expectativa simples para as dimensões nucleares. Se um núcleo atômico é constituído basicamente por prótons e nêutrons e tratássemos os mesmos como esferas duras, de raio r, impenetráveis, empacotadas em uma esfera maior, o número de nucleons (nome genérico para prótons e nêutrons) que caberiam em uma esfera de raio R seria, aproximadamente:
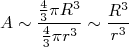 (1)
(1)Desse modo, é natural esperar que o raio nuclear, considerando o núcleo esférico, seja proporcional à raiz cúbica do número atômico, ou seja:
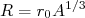 (2)
(2)Sendo
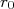 uma constante de proporcionalidade, determinada experimentalmente. Vamos ver, a seguir, que para a grande maioria dos núcleos, essa correlação é verdadeira, com
uma constante de proporcionalidade, determinada experimentalmente. Vamos ver, a seguir, que para a grande maioria dos núcleos, essa correlação é verdadeira, com  fm.
fm.
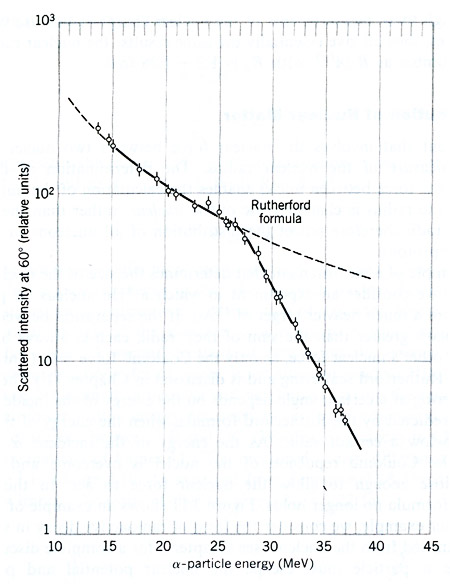
O método mais direto de medida de raio nuclear consiste em utilizar o espalhamento de partículas α por núcleos diversos. Como vimos, quando as energias das partículas α são baixas o suficiente para a distância de máxima aproximação ser tal que não haja superposição dos núcleos, a seção de choque diferencial de espalhamento segue a fórmula de Rutherford. Contudo, aumentando a energia, a distância de máxima aproximação diminui, até o ponto que começa a haver superposição dos núcleos. Quando isso ocorre, o potencial de interação não é mais da forma 1/r e a seção de choque de espalhamento começa a desviar da previsão de Rutherford. A figura 1 ilustra esse processo. Nessa figura temos o espalhamento de partículas α por núcleos de ouro em função da energia da colisão. A partir de um certo ponto, a seção de choque diminui em relação à expressão de Rutherford, indicando que o potencial não é mais da forma 1/r. Experiências conduzidas por Rutherford, Geiger e Mardsen, na década de 1910, já obtiveram resultados para medidas de raio nuclear compatíveis com a expressão (2) com
 fm.
fm.
Um outro método utilizado para medida de raios nucleares consiste na observação de raios-X devido a transições atômicas para a camada K. Vamos olhar, por exemplo, o Raio-X Kα, correspondente à transição atômica do nível 2p para o nível 1s. Para simplificar e tornar o problema factível, vamos considerar transições em átomos de apenas um elétron e também desconsiderar correções nos níveis de energia devido a efeitos relativísticos. Contudo, essas correções são consideradas em análises de dados reais obtidos.
Em átomos de um elétron, as componentes radiais das funções de onda dos níveis 1s e 2p são, respectivamente:
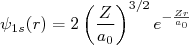 (3)
(3)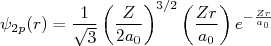 (4)
(4)Com
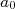 sendo o raio de Bohr, dado por:
sendo o raio de Bohr, dado por:
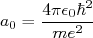 (5)
(5)Essas funções de onda são obtidas considerando o núcleo pontual. Vamos também assumir que o núcleo é muito pequeno e que as suas dimensões não alterem significativamente as formas das funções de onda.
O método consiste em observar a diferença de energia entre os raios-X Kα de dois isótopos diferentes, com números atômicos A e A'. A diferença de energia entre esses raios-X vale:
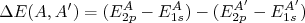 (6)
(6)Se os núcleos fossem pontuais, essa diferença seria nula. Contudo, considerando o núcleo como sendo uma esfera de raio
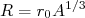 , no qual, o potencial coulombiano para
, no qual, o potencial coulombiano para 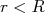 vale:
vale:
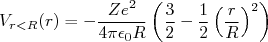 (7)
(7)Essa diferença não é nula, pois existe uma diferença entre os raios nucleares dos isótopos. Considerando que a componente cinética das energias não se alterem entre um núcleo e outro, já que estamos considerando as funções de onda inalteradas, a expressão (6) se reduz a diferenças entre valores médios de potenciais, ou seja:
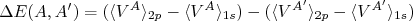 (8)
(8)Sendo:
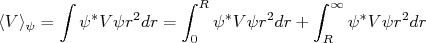 (9)
(9)Em primeira aproximação, as integrais para r > R se anulam, pois nesse caso os potenciais são praticamente os mesmos. Resta-nos calcular os valores médios dos potenciais para r < R. No caso das ondas 2p, como a função de onda, conforme eq. (4) vai a zero para raios pequenos, podemos também desprezá-las no cálculo de ΔE. Assim, resta-nos escrever que:
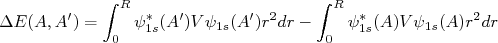 (10)
(10)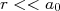 , podemos fazer que
, podemos fazer que 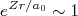 . Assim, usando a equação (2) para o raio nuclear, pode-se deduzir que:
. Assim, usando a equação (2) para o raio nuclear, pode-se deduzir que:
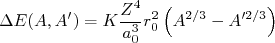 (11)
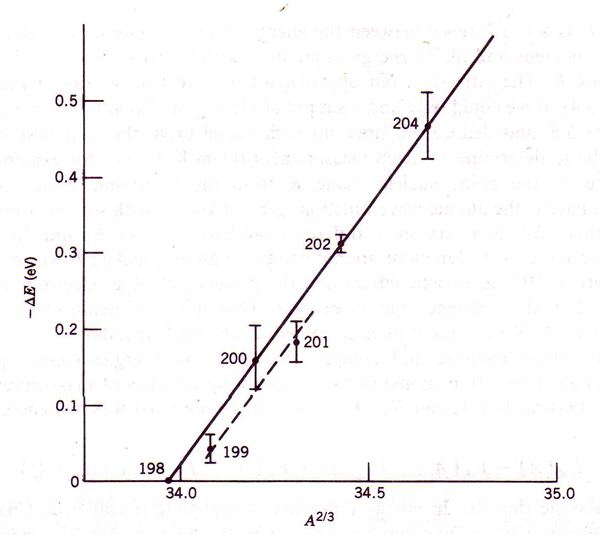
(11)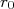 . A figura 2 mostra medidas de ΔE em função de A2/3 para isótopos de mercúrio. Vemos claramente a linearidade da dependência. A diferença entre isótopos com A pares e ímpares vem do fato de haver uma partícula desemparelhada, com função de onda mais espalhada espacialmente, acarretando em um raio ligeiramente maior.
. A figura 2 mostra medidas de ΔE em função de A2/3 para isótopos de mercúrio. Vemos claramente a linearidade da dependência. A diferença entre isótopos com A pares e ímpares vem do fato de haver uma partícula desemparelhada, com função de onda mais espalhada espacialmente, acarretando em um raio ligeiramente maior.
O principal problema desse método é o fato de
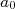 ser muito grande, se comparado ao raio nuclear. Nesse caso, os valores de ΔE são muito pequenos e difíceis de serem medidos. Uma alternativa consiste de medir a diferença de energia entre raios-X de átomos muônicos. Átomos muônicos são aqueles nos quais os elétrons são substituídos por múons. Isso pode ser feito em experimentos com aceleradores de partículas. Múons são criados nesses aceleradores e podem ser capturados por átomos. O múom é um lépton, assim como o elétron, porém sua massa é cerca de 200 vezes maior. Da expressão (5) podemos ver que o valor de
ser muito grande, se comparado ao raio nuclear. Nesse caso, os valores de ΔE são muito pequenos e difíceis de serem medidos. Uma alternativa consiste de medir a diferença de energia entre raios-X de átomos muônicos. Átomos muônicos são aqueles nos quais os elétrons são substituídos por múons. Isso pode ser feito em experimentos com aceleradores de partículas. Múons são criados nesses aceleradores e podem ser capturados por átomos. O múom é um lépton, assim como o elétron, porém sua massa é cerca de 200 vezes maior. Da expressão (5) podemos ver que o valor de 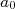 para um átomo muônico é muito menor que o átomo eletrônico. Note que, na expressão (11), ΔE depende do inverso ao cubo de
para um átomo muônico é muito menor que o átomo eletrônico. Note que, na expressão (11), ΔE depende do inverso ao cubo de 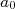 . Assim, a medida de ΔE com átomos muônicos é muito mais precisa que aquelas realizadas com átomos eletrônicos.
. Assim, a medida de ΔE com átomos muônicos é muito mais precisa que aquelas realizadas com átomos eletrônicos.
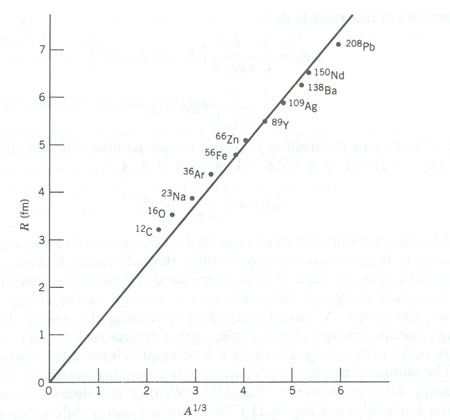
A figura 3 mostra medidas de raios nucleares obtidas a partir da medida de raios-X de átomos muônicos. Note a clara dependência com A1/3. Um ajuste passando pela orígem retorna
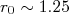 fm, muito próximo ao valor obtido por espalhamento de partículas α.
fm, muito próximo ao valor obtido por espalhamento de partículas α.
Há outros métodos para medidas de raios nucleares, tais como medidas de decaimento nuclear em partículas α, medidas de energia coulombiana, etc. Esses métodos pressupõem uma distribuição conhecida de carga no núcleo, como fizemos no caso de medidas de raios-X, assumindo que o núcleo é uma esfera uniformemente carregada com bordas bem definidas. Essa hipótese é razoável? Como a carga nuclear está distribuída no núcleo?
Para responder essas perguntas, pesquisadores da Universidade de Stanford, nos anos de 1950, desenvolveram uma técnica experimental capaz de revelar a distribuição de carga elétrica no núcleo. Essa técnica consiste na medida da seção de choque de espalhamento de elétrons no núcleo. Lembre-se contudo que para efeitos ondulatórios serem significativos, o comprimento de onda de de Broglie para o elétron deve ser da ordem de grandeza da dimensão que se quer investigar. Sabemos que a seção de choque diferencial de espalhamento, de acordo com a aproximação de Born está relacionada com a transformada de Fourier do potencial de interação, ou seja:
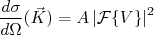 (12)
(12)sendo
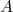 uma constante de proporcionalidade, facilmente calculável. A interação de elétrons com o núcleo é eletromagnética. Considerando o núcleo atômico como possuindo uma distribuição espacial de carga
uma constante de proporcionalidade, facilmente calculável. A interação de elétrons com o núcleo é eletromagnética. Considerando o núcleo atômico como possuindo uma distribuição espacial de carga 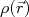 , de tal forma que:
, de tal forma que:
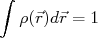 (13)
(13)O potencial de interação
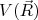 vale:
vale:
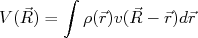 (14)
(14)onde
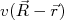 é o potencial de interação entre o elétron na posição
é o potencial de interação entre o elétron na posição 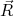 e a carga pontual
e a carga pontual  localizada na posição
localizada na posição 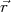 . Podemos ver que o potencial de interação é a função convolução entre a função de distribuição de carga
. Podemos ver que o potencial de interação é a função convolução entre a função de distribuição de carga 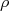 e o potencial de interação
e o potencial de interação  . Usando o teorema da convolução, no qual a transformada de Fourier da convolução de duas funções
. Usando o teorema da convolução, no qual a transformada de Fourier da convolução de duas funções 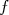 e
e 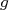 pode ser dada por:
pode ser dada por:
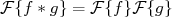 (15)
(15)temos que:
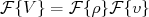 (16)
(16)Substituindo (16) em (12), chegamos à:
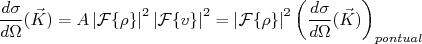 (16)
(16)Isto é, a seção de choque diferencial de espalhamento por uma distribuição de carga é equivalente à seção de choque diferencial de espalhamento do elétron por uma carga pontual
 , facilmente calculável, modificada por um fator
, facilmente calculável, modificada por um fator 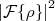 . Com base nisso, define-se o fator de forma,
. Com base nisso, define-se o fator de forma, 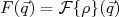 como sendo:
como sendo:
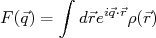 (17)
(17)sendo
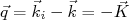 , a mudança de momento do elétron espalhado. Por definição, o fator de forma é normalizado de modo que
, a mudança de momento do elétron espalhado. Por definição, o fator de forma é normalizado de modo que 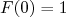 . Assim, medindo-se a seção de choque de espalhamento em vários ângulos para várias energias de colisão, pode-se mapear experimentalmente
. Assim, medindo-se a seção de choque de espalhamento em vários ângulos para várias energias de colisão, pode-se mapear experimentalmente 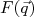 e, através da sua transformada inversa de Fourier, obtém-se
e, através da sua transformada inversa de Fourier, obtém-se 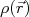 .
.
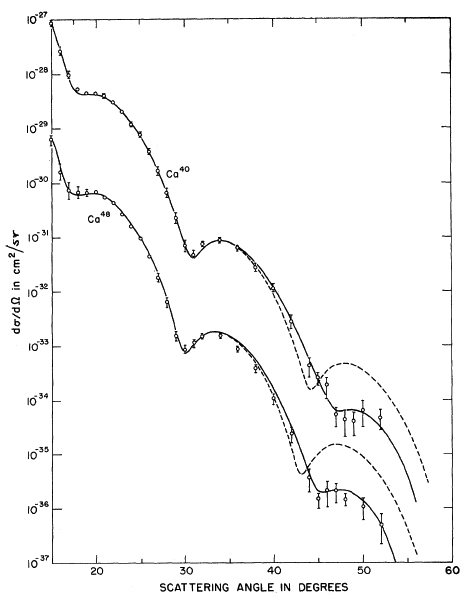
A figura 4 mostra seções de choque de espalhamento de elétrons por isótopos de cálcio. Note o padrão similar aquele observado em figuras de difração óptica. Os mínimos locais não vão a zero devido a vários efeitos mas, principalmente devido à forma difusa da superfície nuclear, como veremos a seguir. Dessa figura pode-se obter o fator de forma nuclear e, a partir da sua transformada inversa de Fourier, obter a distribuição espacial de carga.
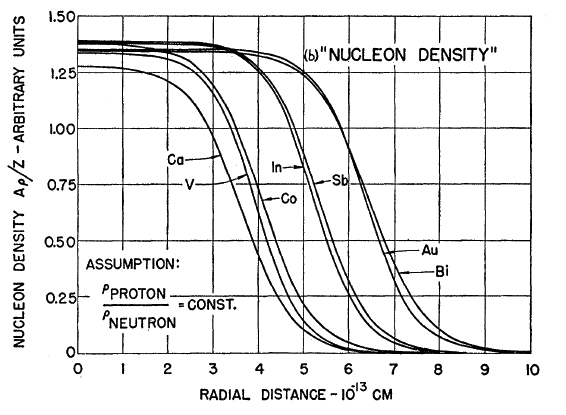
A figura 5 mostra a distribuição de carga obtida para vários núcleos. Nessa figura, o eixo-y mostra a densidade de carga normalizada pela razão A/Z para cada núcleo. Note que a densidade de carga no interior do núcleo é praticamente a mesma. Dessa figura pode-se extrair que os núcleos apresentados possuem distribuições de carga aproximadamente esféricas, porém com superfícies difusas. Contrário ao senso comum, no qual esperávamos que os prótons, devido a repulsão coulombiana, estivessem mais concentrados na superfície nuclear, eles estão distribuídos em todo o volume nuclear. Uma sistemática para núcleos mais pesados (A>20) mostra que podemos escrever que a densidade de carga pode ser descrita por uma distribuição de Fermi do tipo:
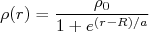 (18)
(18)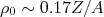 fm-3 é a densidade máxima de distribuição de carga.
fm-3 é a densidade máxima de distribuição de carga. 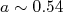 fm corresponde à difusividade da superfície nuclear. A espessura na qual a densidade cai de 90% a 10% do valor máximo equivale a
fm corresponde à difusividade da superfície nuclear. A espessura na qual a densidade cai de 90% a 10% do valor máximo equivale a 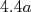 .
. 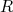 corresponde ao raio no qual a densidade é metade do seu valor máximo. O ajuste sistemático dos dados não passa pela orígem quando A tende a zero. Isso é devido ao fato de núcleos leves possuirem poucos nucleons, e assim, ser difícil associar uma distribuição de carga como a mostrada em (18). Contudo, fazendo um ajuste de
corresponde ao raio no qual a densidade é metade do seu valor máximo. O ajuste sistemático dos dados não passa pela orígem quando A tende a zero. Isso é devido ao fato de núcleos leves possuirem poucos nucleons, e assim, ser difícil associar uma distribuição de carga como a mostrada em (18). Contudo, fazendo um ajuste de 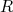 forcando-o a passar pela orígem resulta em:
forcando-o a passar pela orígem resulta em:
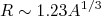 (19)
(19)Note a similaridade dos resultados obtidos em todos os métodos apresentados. O mais importante, todavia, é a similaridade entre os resultados obtidos com pontas de prova eletromagnéticas (espalhamento de elétrons, átomos muônicos), onde a medida é sensível à distribuição de carga, com aquelas obtidas por pontas de prova nucleares (espalhamento de partículas α por exemplo). Essas últimas são sensíveis a distribuição de matéria nuclear como um todo. Conclui-se, dai, que a distribuição de prótons e nêutrons no núcleo, salvo alguns núcleos com características exóticas, é muito similar.
Exercícios
- Obtenha o raio nuclear para a reação cujas seções de choque são mostradas na figura 1.
- Deduza a expressão (11) a partir da expressão (10). Obtenha o valor da constante K. Qual a razão típica para
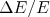 para isótopos naturais de Hg? E no caso de átomos muônicos de Hg?
para isótopos naturais de Hg? E no caso de átomos muônicos de Hg?
- Qual deve ser a energia típica de um feixe de elétrons para realizar medidas de distribuição de carga para núcleos com A ~ 100?
- Obtenha o fator de forma nuclear para uma distribuição na qual
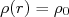 , se
, se 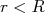 e 0, se
e 0, se 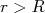 . Faça o gráfico do fator de forma em função do ângulo de espalhamento, assumindo que a colisão é elástica.
. Faça o gráfico do fator de forma em função do ângulo de espalhamento, assumindo que a colisão é elástica.
- Compute o número de nucleons distribuídos em
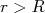 , utilizando a equação (18) para o núcleo de 120Sn.
, utilizando a equação (18) para o núcleo de 120Sn.
Leitura recomendada
- Fundamentals of nuclear physics, N. A. Jelley, capítulo 1.2.
- Introductory nuclear physics, K. S. Krane, capítulo 3.1.
- Nuclear and Particle Physics, W. S. C. Williams, capítulo 3.
two comments
Eu nunca fiz a conta explicitamente para aquele potencial mas ele não deve reproduzir bem os dados por conta de haver também a interação forte adicionada à coulombiana. O potencial mais simples que se pode utilizar para descrever a interação forte (e é utilizado com razoável sucesso) é um poço radial, ou seja, V = -V0 para r < R e V = 0 para r > R. Adicione isso ao potencial coulombiano e você tem o potencial de interação total.




Suaide, na experiência de Rutherford sobre a investigação do tamanho nuclear, a fórmula para a seção de choque com potencial 1/r deixa de valer para distâncias de máxima aproximação menores que 1.2 fm, e, segundo a figura (1), passa a ter um comportamento linear com a energia. É possível reproduzir esse comportamento para a seção de choque utilizando o potencial da fórmula (7)? Senão, qual o potencial que descreve a interação das partículas alfa (que interagem fortemente?) com o núcleo?