Propagação de incertezas
Em algumas situações a avaliação de incertezas pode ser feita na força bruta, simplesmente através da repetição de um experimento e avaliação dos desvios padrão da amostra obtida. Por exemplo, imagine-se jogando um balão de água do alto de uma torre. Você pode medir o tempo de queda deste balão e, através de um cálculo simples, supondo o movimento como sendo uniformemente variado e partindo do repouso, calcular a aceleração deste balão. Pois bem, para avaliar a incerteza nesta aceleração simplesmente repete-se à exaustão o experimento. Para cada balão jogado calcula-se a aceleração. No final, calcula-se a média das acelerações, desvio padrão e desvio padrão da média. Tem-se, portanto, o valor médio da aceleração e sua incerteza. O que aconteceu, de fato, é que a flutuação no tempo de queda do balão gerou uma flutuação na aceleração medida (veja a figura 1). Essas flutuações foram avaliadas simplesmente através da repetição da medida.
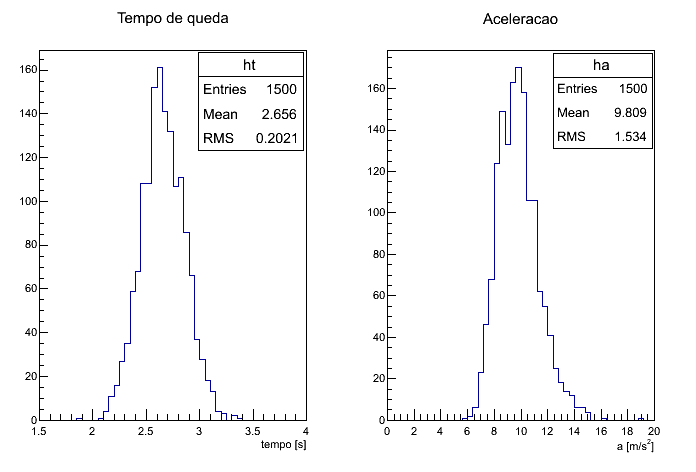
Figura 1 - Histograma com dados de um experimento de queda repetido 1500 vezes. A flutuação na medida de tempo gera uma flutuação no valor calculado de aceleração.
Por outro lado, em muitas situações não é possível repetir a medida à exaustão de forma a avaliar essas flutuações e o impacto delas em grandezas derivadas. Em uma situação bem simples, tem-se a medida
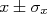 e quer-se calcular a grandeza
e quer-se calcular a grandeza 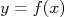 , derivada, bem como sua incerteza
, derivada, bem como sua incerteza 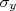 . O cálculo de
. O cálculo de  é simples, basta substituir o valor de
é simples, basta substituir o valor de  na função
na função 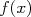 . Mas como eu calculo
. Mas como eu calculo 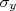 conhecendo
conhecendo 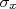 ? Para isso precisamos aprender a fazer propagações de incertezas. O objetivo deste texto é deduzir uma expressão para propagação de incertezas e discutir alguns exemplos simples.
? Para isso precisamos aprender a fazer propagações de incertezas. O objetivo deste texto é deduzir uma expressão para propagação de incertezas e discutir alguns exemplos simples.
Fórmula geral de propagação de incertezas
Em um caso geral, digamos que eu tenho medidas de vários observáveis (por exemplo, altura e largura de uma folha de papel) e quero calcular uma grandeza derivada (por exemplo, a área desta folha). Conheço as incertezas dessas medidas e quero calcular a incerteza na grandeza derivada (por exemplo, a incerteza na área da folha). Para estabelecer uma notação, vamos denominar as grandezas observáveis como sendo
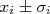 e a grandeza derivada como sendo
e a grandeza derivada como sendo 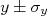 , que pode ser calculada através do uso de uma fórmula
, que pode ser calculada através do uso de uma fórmula 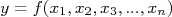 . Neste caso,
. Neste caso, 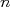 é o número de grandezas observáveis que tenho à disposição.
é o número de grandezas observáveis que tenho à disposição. Na força bruta, para calcular a incerteza em
 , simplesmente repetiríamos a medida do conjunto
, simplesmente repetiríamos a medida do conjunto 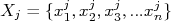 um determinado número de vezes (
um determinado número de vezes (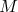 ) e calcularíamos
) e calcularíamos 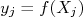 para cada repetição. No final, a variância (quadrado do desvio padrão) de
para cada repetição. No final, a variância (quadrado do desvio padrão) de  poderia ser calculado como:
poderia ser calculado como: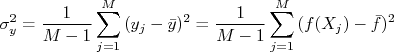
Agora temos somente um conjunto de medidas e, por conta disso, apenas um valor para
 . Porém, conhecemos o conjunto de incertezas das grandezas
. Porém, conhecemos o conjunto de incertezas das grandezas 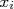 , dado por
, dado por 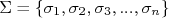 . Para calcular a incerteza em
. Para calcular a incerteza em  vamos admitir que as incertezas em
vamos admitir que as incertezas em 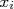 são pequenas o suficiente para que possamos aproximar a função
são pequenas o suficiente para que possamos aproximar a função 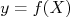 por uma reta por em torno de
por uma reta por em torno de 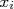 em um intervalo da ordem de
em um intervalo da ordem de 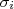 para mais e para menos. A inclinação desta reta ao longo da variável
para mais e para menos. A inclinação desta reta ao longo da variável 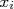 é dada pela derivada parcial de
é dada pela derivada parcial de 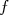 em relação à
em relação à 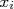 (ver figura 2). Deste modo, podemos escrever a função
(ver figura 2). Deste modo, podemos escrever a função 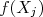 como sendo, aproximadamente:
como sendo, aproximadamente: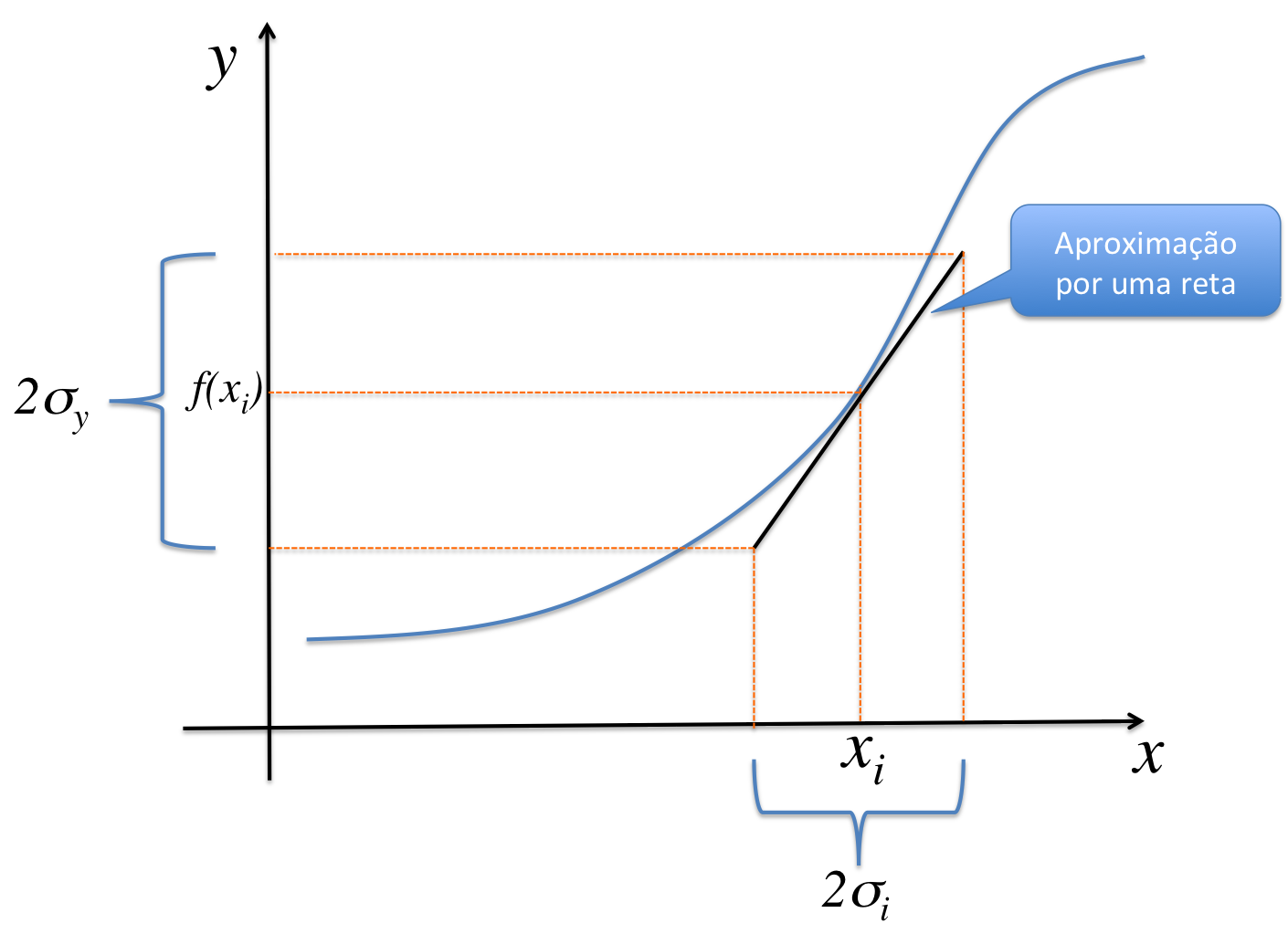
Figura 2 - Aproximação de uma função por uma reta em um ponto qualquer e como uma variação em x gera uma variação em y.
A equação desta reta é:
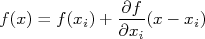
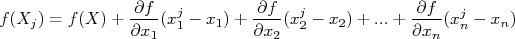
Qué é uma expansão em série de Taylor de primeira ordem. Como só temos um conjunto de medidas, vamos também aproximar que o valor médio de
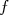 é aquele calculado em
é aquele calculado em 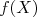 , ou seja,
, ou seja, 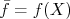 . Substituindo isso, bem como a expansão em série de Taylor, na expressão para o desvio padrão de
. Substituindo isso, bem como a expansão em série de Taylor, na expressão para o desvio padrão de  , temos que:
, temos que: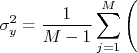 |
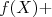 |
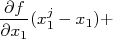 | |
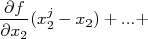 | |
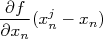 | |
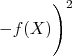 |
Expandindo o quadrado na somatória, temos:
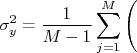 |
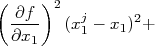 |
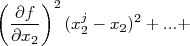 | |
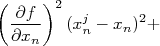 | |
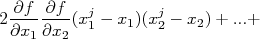 | |
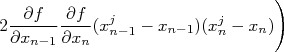 |
Como as derivadas são constantes para a somatória, podemos rearranjar a expressão acima de forma que:
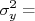 |
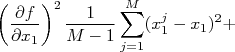 |
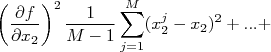 | |
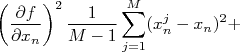 | |
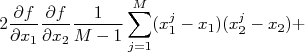 | |
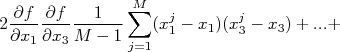 | |
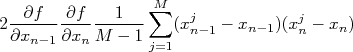 |
Na expressão acima, temos dois tipos de somatória. O primeiro deles tem a forma:
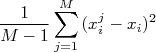
Que nada mais é do que a definição da variância (
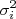 ) do observável
) do observável 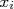 .
. O segundo tipo de somatória tem a forma:
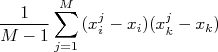
Esse termo é chamado de covariância (
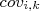 ) e será discutido em momento oportuno.
) e será discutido em momento oportuno. Substituindo essas definições de variância e covariância, temos que:
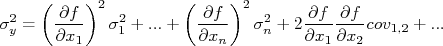
Em resumo, podemos escrever que:
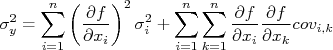
Que é a expressão geral para propagação de incertezas. Se os observáveis
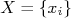 forem todos independentes um do outro, os termos de covariância são nulos e a expressão acima fica mais simplificada na forma:
forem todos independentes um do outro, os termos de covariância são nulos e a expressão acima fica mais simplificada na forma:
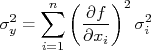
Ou seja, para propagar as incertezas de observáveis para uma grandeza derivada desses observáveis, basta calcular todas as derivadas parciais e substituir na expressão acima. Em algumas situações esses cálculos são bastante complexos então uma análise da contribuição relativa de cada observável na incerteza final pode poupar um trabalho enorme.
Um exemplo
Vamos dizer que alguém mediu tempo de queda de um balão de uma altura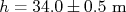 e obteve que
e obteve que 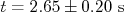 . Usando um modelo simples de queda livre, pode-se deduzir que a aceleração vale:
. Usando um modelo simples de queda livre, pode-se deduzir que a aceleração vale: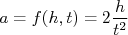 .
.
Substituindo os valores de
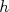 e
e 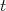 na expressão acima obtém-se que
na expressão acima obtém-se que 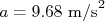 . Qual a incerteza na aceleração? Os nossos observáveis, neste caso, são
. Qual a incerteza na aceleração? Os nossos observáveis, neste caso, são 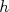 e
e 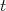 e são medidos independentemente, de forma que a covariância entre eles é nula. Assim, podemos escrever que a incerteza em
e são medidos independentemente, de forma que a covariância entre eles é nula. Assim, podemos escrever que a incerteza em  ao quadrado vale:
ao quadrado vale: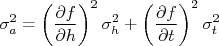
As derivadas são, respectivamente:
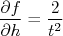
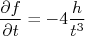
de modo que, substituindo essas derivadas na expressão para a incerteza, temos:
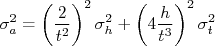
Então basta substituir os valores nesta expressão (
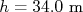 ,
, 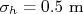 ,
, 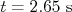 e
e 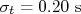 ),e obter que:
),e obter que: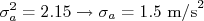
Ou seja:
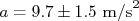
Compare este resultado com o desvio padrão (RMS) no histograma da aceleração na figura 1.
Outro exemplo
Alguém mediu o tamanho de uma sala e obteve para a largura e comprimento, respectivamente, e
e  . A área desta sala é
. A área desta sala é 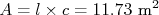 . Qual a incerteza nesta área? A área depende de duas medidas, a largura e o comprimento, de modo que a incerteza na área é:
. Qual a incerteza nesta área? A área depende de duas medidas, a largura e o comprimento, de modo que a incerteza na área é:
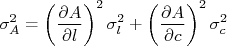
As derivadas são, respectivamente:
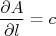
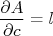
de modo que, substituindo essas derivadas na expressão para a incerteza, temos:
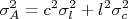
Substituindo os valores, obtemos que:
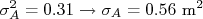
Ou seja:
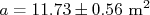
Exercícios
- Mostre que, se
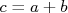 ou
ou 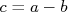 , a incerteza em
, a incerteza em  pode ser escrita como:
pode ser escrita como: 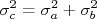 .
.
- Mostre que, se
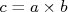 ou
ou 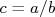 , a incerteza em
, a incerteza em  pode ser escrita como:
pode ser escrita como: 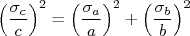 .
.
- O volume,
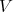 de uma esfera pode ser obtido a partir do seu diâmetro
de uma esfera pode ser obtido a partir do seu diâmetro 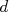 , determinado experimentalmente. Mostrar que a incerteza no volume pode ser obtida da expressão:
, determinado experimentalmente. Mostrar que a incerteza no volume pode ser obtida da expressão: 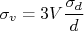 .
.
- O ângulo de Brewster de um material foi medido experimentalmente e obteve-se
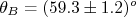 . O índice de refração deste material pode ser obtido a partir da expressão
. O índice de refração deste material pode ser obtido a partir da expressão 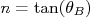 . Obtenha o valor do índice de refração e sua incerteza.
. Obtenha o valor do índice de refração e sua incerteza.
- Uma caixa retangular tem largura, altura e profundidade, respectivamente (em cm):
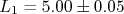 ,
, 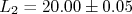 e
e 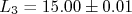 . Determine o volume desta caixa e sua incerteza.
. Determine o volume desta caixa e sua incerteza.
- Um pêndulo de comprimento
 teve o seu período de oscilação medido em
teve o seu período de oscilação medido em 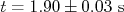 com o objetivo de determinar o valor da aceleração da gravidade. Sabendo que o período de um pêndulo simples pode ser dado por
com o objetivo de determinar o valor da aceleração da gravidade. Sabendo que o período de um pêndulo simples pode ser dado por 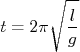 , determine a aceleração da gravidade
, determine a aceleração da gravidade 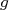 e sua incerteza.
e sua incerteza.
- A velocidade de queda de um paraquedista pode ser calculada por
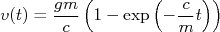 onde
onde 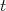 é o instante de tempo,
é o instante de tempo, 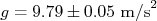 é a aceleração da gravidade,
é a aceleração da gravidade, 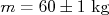 é a massa do paraquedista e
é a massa do paraquedista e 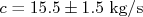 é uma constante que estabelece o arrasto do paraquedas. Calcule a velocidade de queda do paraquedista, com sua incerteza, para
é uma constante que estabelece o arrasto do paraquedas. Calcule a velocidade de queda do paraquedista, com sua incerteza, para 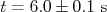 .
.




No comments