Extraindo coeficientes de gráficos
Em muitas situações durante a análise de um gráfico, independente do tipo de escala, observamos comportamentos aparentemente lineares. Nestas situações é razoavelmente simples obter a expressão matemática que representa este comportamento sem a necessidade de utilizar métodos sofisticados ou programas de computador, utilizando apenas régua e operações simples de uma calculadora. Vamos ver como fazer isso.
A ideia geral
Suponha qu a gente tenha um conjunto de dados qualquer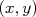 com suas respectivas incertezas. Após uma escolha adequada, seja através de uma mudança explícita de variáveis ou uma escolha de tipo de escala (log, por exemplo), obtém-se um gráfico com comportamento linear. Vamos denominar os eixos deste gráfico como
com suas respectivas incertezas. Após uma escolha adequada, seja através de uma mudança explícita de variáveis ou uma escolha de tipo de escala (log, por exemplo), obtém-se um gráfico com comportamento linear. Vamos denominar os eixos deste gráfico como 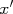 e
e 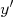 , conforme a figura abaixo (o gráfico está sem escala para ser bem genérico):
, conforme a figura abaixo (o gráfico está sem escala para ser bem genérico):
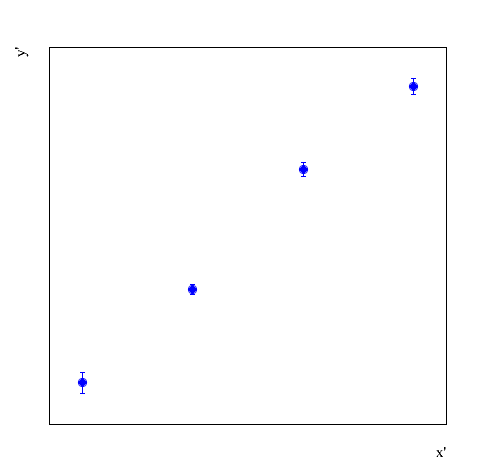
Com uma régua, desenha-se a reta que visualmente descreva o comportamento dos dados mostrados, como mostamos na próxima figura:
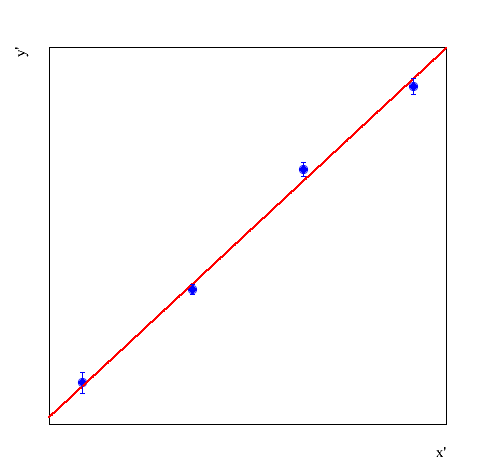
A reta desenhada na figura acima, em vermelho, pode ser parametrizada por uma expressão do tipo
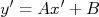 (note as variáveis linha). Para determinar os valores de
(note as variáveis linha). Para determinar os valores de 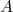 e
e 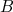 escolhemos dois pontos quaisquer nesta reta (de preferência bem distantes um do outro), conforme mostra a figura abaixo. Vamos denominar estes pontos com as coordenadas
escolhemos dois pontos quaisquer nesta reta (de preferência bem distantes um do outro), conforme mostra a figura abaixo. Vamos denominar estes pontos com as coordenadas 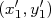 e
e 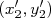 .
.
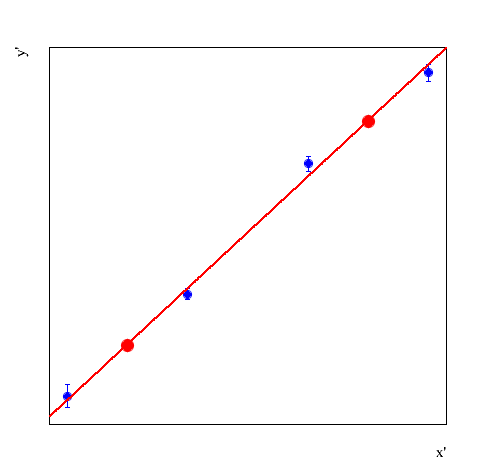
Dos valores destes pontos, podemos calcular
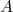 através de:
através de: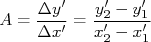
O valor de
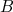 é aquele assumido pela reta quando
é aquele assumido pela reta quando 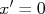 . Em algumas situações as escalas no gráfico não permitem visualizar esta posição no gráfico. Neste caso, toma-se um dos pontos marcados e substitui-se o valor obtido para
. Em algumas situações as escalas no gráfico não permitem visualizar esta posição no gráfico. Neste caso, toma-se um dos pontos marcados e substitui-se o valor obtido para 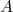 , ou seja, tomando o ponto
, ou seja, tomando o ponto 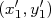 , podemos escrever:
, podemos escrever:
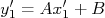
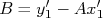
Como o tipo de escala é considerado
O esquema de obtenção de coeficientes de retas valem para todos os tipos de escalas gráficas, bastando apenas prestar atenção em quem são as constantes que serão determinadas e quais são as mudanças de variáveis implícitas nas escalas utilizadas. Vamos examinar 3 tipos de gráficos bastante comuns: o linear-linear (ou milimetrado), o linear-log (mono-log) e o log-log (di-log).O gráfico linear-linear
No gráfico linear-linear (ou milimetrado), não há mudança implícita no desenho da escala no papel, ou seja
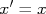 e
e 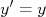 . Veja um exemplo abaixo.
. Veja um exemplo abaixo.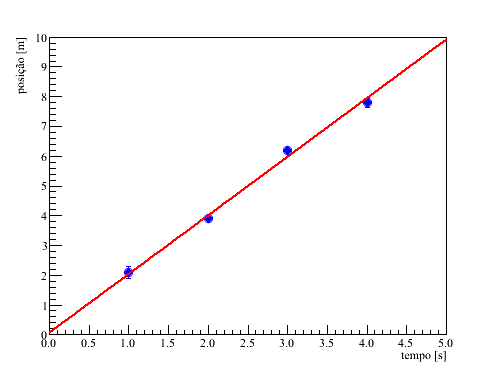
A função que melhor descreve os dados no gráfico é
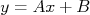 . Vamos determinar os valores destes coeficientes. Neste caso, tomemos dois pontos quaisquer na reta ajustada
. Vamos determinar os valores destes coeficientes. Neste caso, tomemos dois pontos quaisquer na reta ajustada 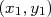 e
e 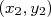 . O coeficiente angular deste gráfico vale, então:
. O coeficiente angular deste gráfico vale, então:
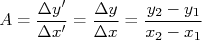
e o coeficiente linear corresponde ao valor de
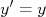 quando
quando 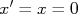 . Se não for possível fazer a leitura direta deste ponto no gráfico, fazemos:
. Se não for possível fazer a leitura direta deste ponto no gráfico, fazemos:
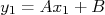
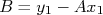
O gráfico linear-log
Em algumas situações um dos eixos do gráfico está em escala logarítmica. Pode ser o eixo x ou o eixo y, tanto faz. Neste caso, há uma mudança implícita na escala deste eixo, já que a distância ao longo do eixo no gráfico é proporcional ao logaritmo da grandeza que está sendo representada no eixo. Vou tratar aqui apenas do caso no qual este eixo é o eixo y. Mas a mesma ideia se aplica no outro eixo. Um exemplo é mostrado abaixo.
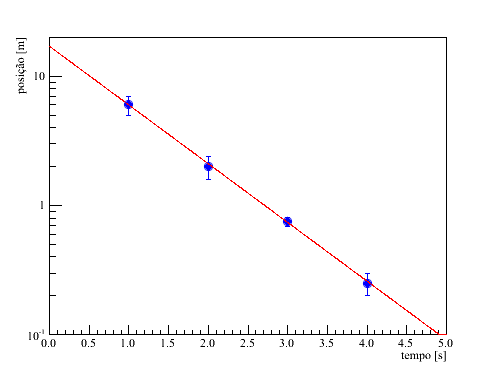
Note que os dados seguem uma tendência visual de uma reta nesta escala. Sabendo que a mudança implícita de variáveis que esta escala proporciona é
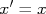 e
e 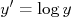 , qual a função que, quando desenhada nesta escala, assume a aparência de reta? Vamos tomar a função:
, qual a função que, quando desenhada nesta escala, assume a aparência de reta? Vamos tomar a função:
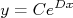
Vamos agora tomar o logaritmo desta expressão, ou seja:
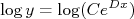
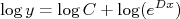
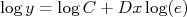
Fazendo a escolha
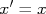 e
e 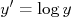 a expressão acima resulta em:
a expressão acima resulta em:
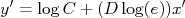
que é uma reta onde
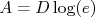 e
e 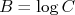 .
.Segundo o nosso padrão, o coeficiente angular é dado por:
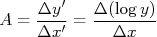
Tomando dois pontos quaisquer na reta ajustada aos dados,
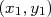 e
e 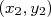 , e substituindo acima (note que, apesar da escala em y ser logarítmica, nós lemos o valor de y diretamente e não o valor do seu logaritmo):
, e substituindo acima (note que, apesar da escala em y ser logarítmica, nós lemos o valor de y diretamente e não o valor do seu logaritmo):
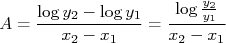
Como
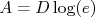 , temos que:
, temos que:
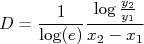
Vamos agora pensar em determinar o valor da constante
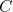 . Sabemos que o valor da constante
. Sabemos que o valor da constante 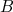 pode ser obtida diretamente do gráfico do valor de
pode ser obtida diretamente do gráfico do valor de 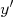 na reta quando
na reta quando 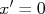 . Como
. Como 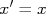 , basta ler o valor na reta que cruza
, basta ler o valor na reta que cruza 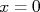 . Como, também, na escala, nós lemos diretamente
. Como, também, na escala, nós lemos diretamente 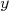 e não o seu logaritmo, o valor da constante
e não o seu logaritmo, o valor da constante 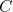 é aquele no qual a reta assume o valor para
é aquele no qual a reta assume o valor para 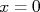 .
.
Quando não for possível fazer esta leitura direta do gráfico, basta aplicar nossa definição para a constante
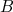 , o que resulta em:
, o que resulta em:
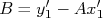
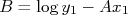
Como
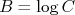 temos que:
temos que:
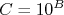
Ou seja, determinamos o valor das constantes
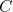 e
e 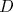 , como queríamos inicialmente.
, como queríamos inicialmente.
O gráfico log-log
Vamos olhar a situação na qual ambos eixos são logarítmicos. Neste caso, as mudanças de variáveis são, implicitamente,
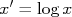 e
e 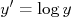 . Um exemplo deste tipo de gráfico é mostrado abaixo.
. Um exemplo deste tipo de gráfico é mostrado abaixo.
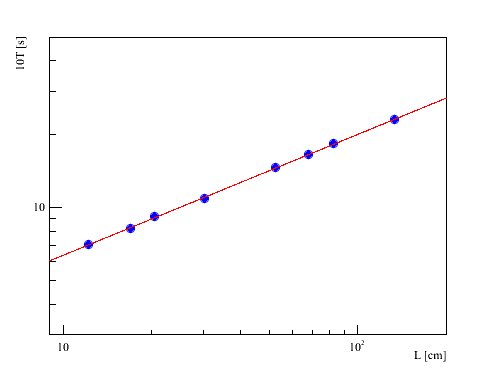
Em algumas situações, como na apresentada acima, o comportamento dos dados, por conta da escolha de escalas, aparenta uma reta. Qual função matemática que, nesta escala, torna-se uma reta? Qual a equação (valores dos parâmetros) desta função (no caso, a linha vermelha)? Vamos tomar a função:
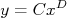
Vamos agora tomar o logaritmo desta expressão, ou seja:
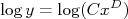
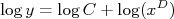
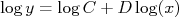
Fazendo a escolha
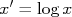 e
e 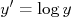 a expressão acima resulta em:
a expressão acima resulta em:
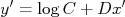
que é uma reta onde
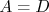 e
e 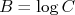 .
.Segundo o nosso padrão, o coeficiente angular é dado por:
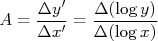
Tomando dois pontos quaisquer na reta ajustada aos dados,
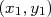 e
e 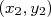 , e substituindo acima (note que, apesar da escala em x ey serem logarítmicas, nós lemos os valores de x e de y diretamente e não o valor dos seus logaritmom):
, e substituindo acima (note que, apesar da escala em x ey serem logarítmicas, nós lemos os valores de x e de y diretamente e não o valor dos seus logaritmom):
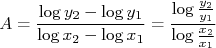
Como
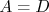 , temos que:
, temos que:
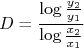
Vamos agora pensar em determinar o valor da constante
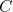 . Sabemos que o valor da constante
. Sabemos que o valor da constante 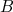 pode ser obtida diretamente do gráfico do valor de
pode ser obtida diretamente do gráfico do valor de 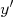 na reta quando
na reta quando 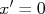 . Como
. Como 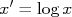 , basta ler o valor na reta que cruza
, basta ler o valor na reta que cruza 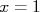 (pois
(pois 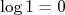 ). Como, também, na escala, nós lemos diretamente
). Como, também, na escala, nós lemos diretamente 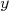 e não o seu logaritmo, o valor da constante
e não o seu logaritmo, o valor da constante 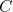 é aquele no qual a reta assume o valor para
é aquele no qual a reta assume o valor para 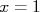 .
.
Quando não for possível fazer esta leitura direta do gráfico, basta aplicar nossa definição para a constante
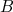 , o que resulta em:
, o que resulta em:
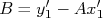
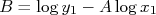
Como
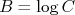 temos que:
temos que:
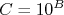
Ou seja, determinamos o valor das constantes
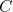 e
e 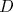 , como queríamos inicialmente.
, como queríamos inicialmente.





Professor, muito obrigado pelo material, ficou muito facil de entender o assunto desse jeito.