Porque quando ω >> ωRC o circuito RC é um integrador?

These icons link to social bookmarking sites where readers can share and discover new web pages.
  • Facebook
  • Google
  • Twitter
Surgiu essa dúvida em um aluno. Vou tentar respondê-la abaixo.

Uma tensão qualquer 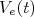V_e(t), por exemplo, uma onda quadrada, pode ser escrita como uma expansão de Fourier, ou seja:

V_e(t) = \sum_{n}{V_{e}^{n} e^{ j \omega_{n} t }

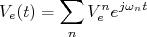
Em um circuito RC, o ganho em função da frequência pode ser escrito como:

G(\omega) = \frac{1}{ \sqrt{1+\left(\frac{\omega}{\omega_{RC}\right)^2}} }

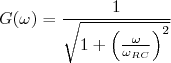
e a fase:

\phi_\omega=\arctan\left( -\frac{\omega}{\omega_{RC}} \right)

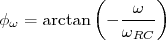
O sinal de tensão de saída, no nosso caso, a tensão no capacitor, corresponde ao ganho aplicado em cada componente da expansão de Fourier, ou seja:

V_C(t) = \sum_{n}{G(\omega_{n}) e^{j\phi_{\omega_n}} V_{e}^{n} e^{ j \omega_{n} t }

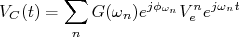
No limite em que 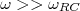\omega>>\omega_{RC}, os ganho e fase acima tornam-se:

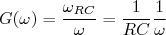G(\omega) = \frac{\omega_{RC}}{ \omega}=\frac{1}{RC}\frac{1}{\omega}       e       \phi_\omega=-\frac{\pi}{2}

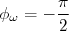
Pois bem, se o sinal de entrada tiver todas as suas componentes de Fourier com 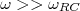\omega>>\omega_{RC}, o que é o caso para uma onda quadrada de \omega>>\omega_{RC}, a tensão no capacitor torna-se:

V_C(t) = \sum_{n}{ \frac{1}{RC}\frac{1}{ \omega_n} e^{-j\frac{\pi}{2}} V_{e}^{n} e^{ j \omega_{n} t } = \sum_{n}{ -\frac{1}{RC}\frac{j}{ \omega_n} V_{e}^{n} e^{ j \omega_{n} t }

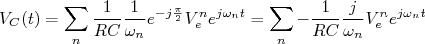
Lembre-se que, para uma onda harmônica simples:

\int{Ve^{j\omega t}dt} = \frac{1}{j\omega}Ve^{j\omega t} = -\frac{j}{\omega}Ve^{j\omega t}

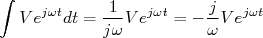
Por comparação, a tensão no capacitor fica:

V_C(t) = \sum_{n}{ \frac{1}{RC}\left(\int{V_{e}^{n} e^{ j \omega_{n} t }dt}\right)

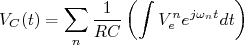
rearranjando os termos:

V_C(t) = \frac{1}{RC}\int{\left(\sum_{n}V_{e}^{n} e^{ j \omega_{n} t }\right)dt} = \frac{1}{RC}\int{V_{e}(t) dt}

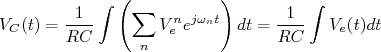
ou seja, no limite de altas frequências, com 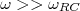\omega>>\omega_{RC}, a tensão no capacitor, a menos da constante 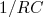1/RC, corresponde à integral no tempo da tensão de entrada.
Alexandre Thursday 10 March 2011 at 8:07 pm | | Linkdump

« Triste notícia | Home | Doses de radiação »