Regra de ouro de Fermi
Notas de aula são propriedade intelectual. Sendo assim, qualquer uso, no todo ou em parte, deve ter a origem referenciada apropriadamente, após autorização de seu autor.
O texto a seguir corresponde à anotações parciais de aula. Não é um texto em forma final, completo e totalmente revisado. Nesse caso, esse texto não tem como objetivo substituir livros sobre o assunto. Assim, esse texto deve ser entendido apenas como um guia de estudo para o aluno acompanhar a disciplina.
A emissão de radiação faz com que um sistema quântico evolua no tempo. A probabilidade de encontrar o sistema em um estado quântico definido decai exponencialmente. A constante de decaimento, relacionada à vida-média do estado, faz com que o sistema não se encontre em uma energia bem definida, e sim a uma superposição de várias energias, resultando em uma distribuição de probabilidade lorentziana. A largura dessa distribuição está diretamente relacionada à vida-média do estado. Por outro lado, se o sistema se encontra em um auto-estado do Hamiltoniano, a evolução temporal possui evolução trivial, dada por
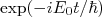 e o sistema deveria permanecer nesse estado indefinidamente. Quando forçamos o estado a decair exponencialmente, estamos sugerindo que o sistema não se encontra mais em um auto-estado do Hamiltoniano (obviamente, a superposição de diferentes energias para descrever essa evolução já confirma isso). Qual a razão para isso ocorrer? O que ocorre para que haja o decaimento do sistema, ou seja, a mudança do estado quântico?
e o sistema deveria permanecer nesse estado indefinidamente. Quando forçamos o estado a decair exponencialmente, estamos sugerindo que o sistema não se encontra mais em um auto-estado do Hamiltoniano (obviamente, a superposição de diferentes energias para descrever essa evolução já confirma isso). Qual a razão para isso ocorrer? O que ocorre para que haja o decaimento do sistema, ou seja, a mudança do estado quântico?
Seja um sistema quântico definido por um estado
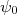 , superposição de auto-estados do Hamiltoniano
, superposição de auto-estados do Hamiltoniano 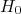 . Se, em determinado momento, um potencial
. Se, em determinado momento, um potencial 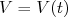 , dependente do tempo, é aplicado ao sistema, o Hamiltoniano, durante o tempo em que esse potencial atua, é modificado e vale:
, dependente do tempo, é aplicado ao sistema, o Hamiltoniano, durante o tempo em que esse potencial atua, é modificado e vale:
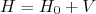 (1)
(1)e assim, o estado
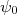 deixa de ter uma evolução temporal trivial. Quando esse potencial deixa de agir, a configuração do estado evoluído pode ser tal que ele se encontre em um estado
deixa de ter uma evolução temporal trivial. Quando esse potencial deixa de agir, a configuração do estado evoluído pode ser tal que ele se encontre em um estado 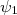 , diferente do inicial. Um exemplo de um potencial desse tipo pode ser uma perturbação devido à radiação eletromagnética ou uma perturbação de natureza fraca, responsável pelo decaimento β de um núcleo. Esperamos que esse potencial seja de natureza perturbativa e que atue em um intervalo finito de tempo. Desse modo, podemos usar teoria de perturbações dependentes do tempo para determinar como é a evolução do sistema.
, diferente do inicial. Um exemplo de um potencial desse tipo pode ser uma perturbação devido à radiação eletromagnética ou uma perturbação de natureza fraca, responsável pelo decaimento β de um núcleo. Esperamos que esse potencial seja de natureza perturbativa e que atue em um intervalo finito de tempo. Desse modo, podemos usar teoria de perturbações dependentes do tempo para determinar como é a evolução do sistema.
Para descrever esse problema, vamos iniciar supondo o conhecimento do Hamiltoniano não perturbado,
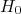 e todos os seus auto-estados
e todos os seus auto-estados 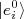 , de modo que:
, de modo que:
 (2)
(2)Podemos escrever o estado inicial do sistema como sendo a superposição de todos possíveis auto-estados de
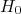 , já que esses formam uma base ortonormal. Assim, em
, já que esses formam uma base ortonormal. Assim, em  o estado quântico pode ser descrito como:
o estado quântico pode ser descrito como:
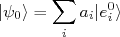 (3)
(3)Sendo esse estado normalizado devemos respeitar:
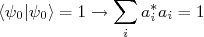 (4)
(4)Durante a ação do potencial perturbativo, o estado evolui. Essa evolução pode ser obtida resolvendo a Equação de Schrödinger dependente do tempo:
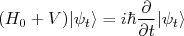 (5)
(5)respeitando a condição de contorno data por (3) no instante inicial. Da mesma forma que escrevemos a condição inicial em (3), podemos escrever a evolução temporal desse estado, de modo a:
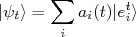 (6)
(6)Substituindo (6) em (5) temos:
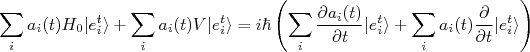 (7)
(7)O primeiro termo do lado esquerdo de (7) e o segundo termo do lado direito corresponde à evolução temporal do estado não perturbado, cancelando um ao outro. Assim, podemos reduzir (7) à:
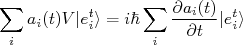 (8)
(8)Podemos fazer o produto interno de (8) com um estado
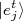 , sabendo que
, sabendo que 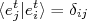 , temos:
, temos:
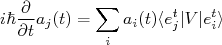 (9)
(9)Como:
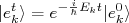 (10)
(10)temos que:
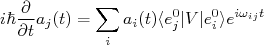 (11)
(11)Sendo:
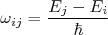 (12)
(12)A equação (11) pode ser escrita em termos de um sistema de equações acopladas. Em termos matriciais, temos que resolver a seguinte equação:
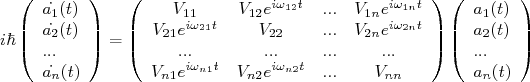 (13)
(13)Com:
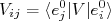 (14)
(14)Resolvendo o sistema de equações em (13), conhecendo-se as condições iniciais, pode-se calcular a evolução temporal do estado e, consequentemente, a probabilidade de encontrá-lo em uma configuração específica em qualquer instante de tempo.
O inconveniente de (13) surge do fato de as equações serem todas acopladas. Muitas vezes o potencial
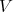 pode ser pequeno e, consequentemente, tratado como uma perturbação. Nesse caso, teoria de perturbação pode ser utilizada para desacoplar as várias equações, tornando a resolução do sistema mais simples.
pode ser pequeno e, consequentemente, tratado como uma perturbação. Nesse caso, teoria de perturbação pode ser utilizada para desacoplar as várias equações, tornando a resolução do sistema mais simples.
A resolução desse sistema, em primeira ordem, é de substituir os coeficientes
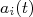 do lado direito da equação pelos seus valores iniciais
do lado direito da equação pelos seus valores iniciais 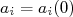 . Desse modo, (13) se reduz a um sistema independente de equações diferenciais de primeira ordem, do tipo:
. Desse modo, (13) se reduz a um sistema independente de equações diferenciais de primeira ordem, do tipo:
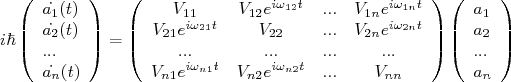 (15)
(15)Integrando (15), resulta, para cada um dos coeficientes
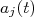 , em primeira ordem:
, em primeira ordem:
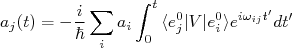 (16)
(16)Sem perder generalização, contudo facilitando o entendimento, podemos supor que no instante inicial o sistema se encontre no estado
 , ou seja, tomamos
, ou seja, tomamos 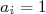 e
e 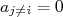 . Desse modo, podemos simplificar (16) para:
. Desse modo, podemos simplificar (16) para:
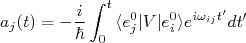 (17)
(17)Vamos calcular a evolução temporal dos coeficientes
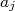 tendo como potencial perturbador uma onda harmônica, ou seja:
tendo como potencial perturbador uma onda harmônica, ou seja:
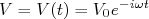 (18)
(18)Esse potencial é especialmente importante em física por representar muito bem interações com partículas, por exemplo, um fóton (ou raio-γ), de frequência
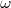 , em uma interação eletromagnética. Representa também uma partícula livre, por exemplo, um elétron (ou pósitron) em um decaimento β. As aplicações desse potencial em física são muito amplas e a resolução de (17) é bastante simples. Aplicando (18) em (17), temos:
, em uma interação eletromagnética. Representa também uma partícula livre, por exemplo, um elétron (ou pósitron) em um decaimento β. As aplicações desse potencial em física são muito amplas e a resolução de (17) é bastante simples. Aplicando (18) em (17), temos:
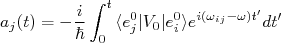 (19)
(19)Cuja solução é trivial e vale:
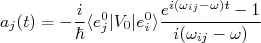 (20)
(20)A probabilidade de encontrar o sistema no estado
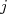 em um instante de tempo qualquer é dado pelo módulo quadrático de
em um instante de tempo qualquer é dado pelo módulo quadrático de 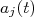 . Assim, tomando (20) e calculando o seu módulo quadrático temos:
. Assim, tomando (20) e calculando o seu módulo quadrático temos:
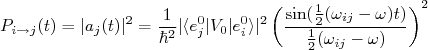 (21)
(21)Como já discutimos anteriormente, as vidas-médias envolvidas nos decaimentos estudados são muito grandes se comparadas aos intervalos típicos dos processos que ocorrem nos núcleos. Nesse caso, estamos interessados no comportamento de (21) para tempos muito longos. Assim, vamos tomar o limite:
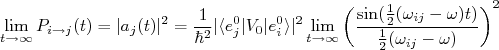 (22)
(22)Usando a relação (ver Quantum Mechanics, Cohen-Tannoudji, apêndice II):
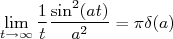 (23)
(23)Podemos escrever (22) como:
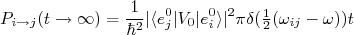 (24)
(24)A dependência linear no tempo do resultado em (24) não supreende. Como resolvemos a evolução em primeira ordem apenas, o aumento na probabilidade de encontrar o estado
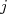 deve variar linearmente no tempo. Usando a definição para
deve variar linearmente no tempo. Usando a definição para 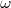 em (12) e a propriedade de funções
em (12) e a propriedade de funções 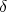 de Dirac:
de Dirac:
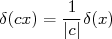 (25)
(25)Podemos reescrever (24) como:
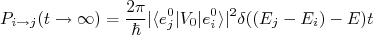 (26)
(26)Sendo
 o equivalente em energia do potencial perturbativo de frequência
o equivalente em energia do potencial perturbativo de frequência 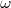 . O resultado em (26) é bastante significativo. A função
. O resultado em (26) é bastante significativo. A função 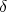 de Dirac assegura que para haver a mudança entre um estado de energia
de Dirac assegura que para haver a mudança entre um estado de energia 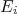 para outro
para outro 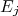 a onda perturbadora deve ter energia igual à diferença de energia dos estados. Esse resultado é amplamente observado em absorção/emissão de radiação por átomos, núcleos, etc. A inclusão de efeitos de ordem superiores resultam em situações similares, porém, a quantidade de energia absorvida/emitida é diferente. No caso de uma correção de segunda ordem, a transição só é permitida através da absorção ou emissão de dois quanta de energia sequencialmente (emissão ou absorção de dois fótons, por exemplo).
a onda perturbadora deve ter energia igual à diferença de energia dos estados. Esse resultado é amplamente observado em absorção/emissão de radiação por átomos, núcleos, etc. A inclusão de efeitos de ordem superiores resultam em situações similares, porém, a quantidade de energia absorvida/emitida é diferente. No caso de uma correção de segunda ordem, a transição só é permitida através da absorção ou emissão de dois quanta de energia sequencialmente (emissão ou absorção de dois fótons, por exemplo).
Como podemos relacionar o resultado em (26) com medidas, como constantes de decaimento
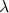 ? Lembrando da aula passada, o número de partículas que surgem no estado
? Lembrando da aula passada, o número de partículas que surgem no estado 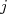 entre um intervalo
entre um intervalo 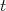 e
e 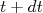 pode ser escrito como:
pode ser escrito como:
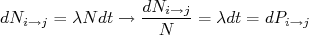 (27)
(27)Note que o sinal negativo desapareceu por conta de não estarmos contando o número de decaimentos e sim o número de filhos que surgem desse decaimento. A razão
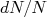 em (27) corresponde à variação na probabilidade em encontrar o sistema no estado
em (27) corresponde à variação na probabilidade em encontrar o sistema no estado 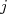 . A partir de (26) podemos calcular essa variação, resultando:
. A partir de (26) podemos calcular essa variação, resultando:
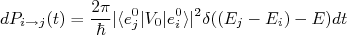 (28)
(28)Comparando (28) com (27) é fácil ver que:
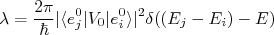 (29)
(29)O resultado apresentado em (29) é muito importante em física e é conhecido como Regra de ouro de Fermi. Esse resultado permite calcular a probabilidade de decaimento entre dois estados. O resultado em (29) é similar ao obtido a partir da aproximação de Born para espalhamento elástico. Não é por acaso. Podemos pensar no espalhamento como sendo uma transição entre dois estados de energia, nesse caso um com vetor de onda
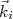 e outro com vetor de onda
. A passagem da partícula pela região de potencial pode ser vista, pelo referencial da partícula, como a presença de um potencial perturbador dependente do tempo, que atua por um intervalo de tempo pequeno (passagem da partícula pela região de interação). A medida de seção de choque é feita assintoticamente, ou seja, em tempos muito longos, se comparado ao tempo de interação. Ou seja, o mesmo que fizemos aqui, porém com outra perspectiva.
e outro com vetor de onda
. A passagem da partícula pela região de potencial pode ser vista, pelo referencial da partícula, como a presença de um potencial perturbador dependente do tempo, que atua por um intervalo de tempo pequeno (passagem da partícula pela região de interação). A medida de seção de choque é feita assintoticamente, ou seja, em tempos muito longos, se comparado ao tempo de interação. Ou seja, o mesmo que fizemos aqui, porém com outra perspectiva.
É comum apresentar a regra de ouro de Fermi de forma mais generalizada. Caso o estado final
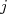 possa ser composto por um número muito grande de estados, pode-se, mostrar, da mesma forma que fizemos para transições entre dois estados simples que:
possa ser composto por um número muito grande de estados, pode-se, mostrar, da mesma forma que fizemos para transições entre dois estados simples que:
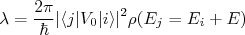 (30)
(30)onde
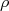 é a densidade de estados que satisfacam a conservação de energia, dada pela função
é a densidade de estados que satisfacam a conservação de energia, dada pela função 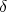 de Dirac. Essa forma de apresentar a regra de ouro de Fermi é útil em diversas situações. Por exemplo, uma situação na qual a perturbação remove a partícula de um estado ligado para um estado livre. Nesse caso, o número de estados finais permitidos podem ser muito grandes e a função de onda final corresponde a uma soma sobre todos esses estados.
de Dirac. Essa forma de apresentar a regra de ouro de Fermi é útil em diversas situações. Por exemplo, uma situação na qual a perturbação remove a partícula de um estado ligado para um estado livre. Nesse caso, o número de estados finais permitidos podem ser muito grandes e a função de onda final corresponde a uma soma sobre todos esses estados.
Leitura recomendada
- Quantum Mechanics, Cohen-Tannoudji, capítulo XIII.
- Introdução à Física Nuclear, H. Schechter e C. A. Bertulani, capítulos 5.9.




No comments