Modelo de Nilsson e rotações nucleares
Notas de aula são propriedade intelectual. Sendo assim, qualquer uso, no todo ou em parte, deve ter a origem referenciada apropriadamente, após autorização de seu autor.
O texto a seguir corresponde à anotações parciais de aula. Não é um texto em forma final, completo e totalmente revisado. Nesse caso, esse texto não tem como objetivo substituir livros sobre o assunto. Assim, esse texto deve ser entendido apenas como um guia de estudo para o aluno acompanhar a disciplina.
Muitos núcleos na tabela periódica possuem características que não são compatíveis com distribuição de matéria nuclear esfericamente simétrica. Por exemplo, os núcleos terra raras possuem, em geral, momentos de quadrupolos elétricos de elevada magnitude. Nesses casos, podemos interpretar esses valores como devidos a estados fundamentais com elevada deformação espacial. Uma explicação qualitativa para que alguns núcleos possuam elevada deformação pode ser obtida através do preenchimento dos últimos nucleons acima da última camada fechada em estados de elevado momento angular orbital. Por exemplo, suponha que o primeiro estado livre após uma camada fechada possua
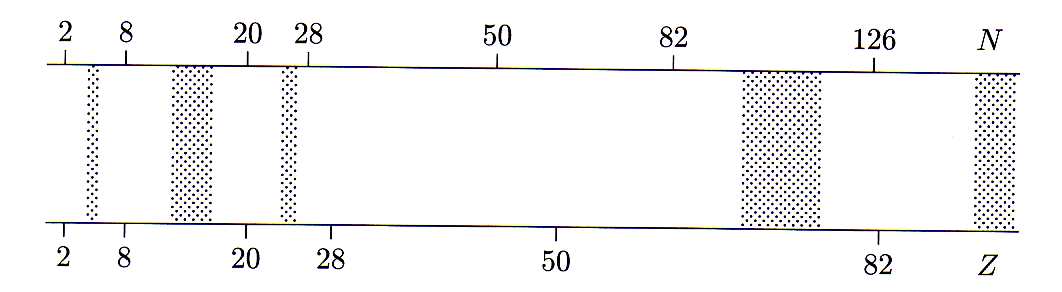
 . O primeiro par de nucleons terá preferência para ocupar os estados
. O primeiro par de nucleons terá preferência para ocupar os estados  e
e  . Isso é devido ao fato de a função de onda desses orbitais serem as mais concentradas espacialmente, promovendo, portanto, uma interação de emparelhamento maior, aumentando a estabilidade do núcleo. Os outros nucleons preencheriam os outros estados de
. Isso é devido ao fato de a função de onda desses orbitais serem as mais concentradas espacialmente, promovendo, portanto, uma interação de emparelhamento maior, aumentando a estabilidade do núcleo. Os outros nucleons preencheriam os outros estados de 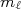 . Porém, esses outros estados não possuem deformação significativa. O resultado seria um sistema final deformado. Assim, em algumas regiões da tabela periódica, os estados finais disponíveis para preenchimento são aqueles de elevado momento angular, gerando grandes deformações nucleares. Na figura 1, as regiões em cinza correspondem a núcleos cujos estados fundamentais apresentam deformações.
. Porém, esses outros estados não possuem deformação significativa. O resultado seria um sistema final deformado. Assim, em algumas regiões da tabela periódica, os estados finais disponíveis para preenchimento são aqueles de elevado momento angular, gerando grandes deformações nucleares. Na figura 1, as regiões em cinza correspondem a núcleos cujos estados fundamentais apresentam deformações.
É de se esperar que, nesses casos, potenciais esfericamente simétricos não correspondam a uma descrição apropriada do sistema. De fato, temos dificuldade em explicar momentos de quadrupolo elétrico desses núcleos com base no modelo de partícula de valência, que supõe que o núcleo possua um caroço esférico e que todo momento de quadrupolo seria devido ao último nucleon desemparelhado. Contudo, um potencial não esférico, representando uma distribuição de matéria nuclear coletivamente deformada, deve ser mais apropriado para explicar essas propriedades desses núcleos.
S. G. Nilsson, em 1955, propôs um modelo de potencial de interação para explicar as propriedades de núcleos deformados. Hoje em dia denominamos esse potencial e, consequentemente, suas previsões, de Modelo de Nilsson. O Modelo de Nilson parte das mesmas hipóteses utilizadas para construir o modelo de camadas extremo com um potencial de interação não esférico e alguns termos de correção.
No modelo de Nilsson, o hamiltoniano de interação pode ser escrito supondo o potencial de interação como o de um oscilador harmônico anisotrópico, ou seja:
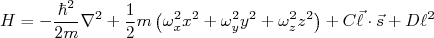 (1)
(1)O termo
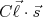 é a correção de acoplamento spin-órbita e o termo
é a correção de acoplamento spin-órbita e o termo  é uma correção para tentar simular um achatamento do potencial do oscilador harmônico e torná-lo mais próximo do potencial real. As constantes desses termos são parâmetros ajustados aos dados experimentais.
é uma correção para tentar simular um achatamento do potencial do oscilador harmônico e torná-lo mais próximo do potencial real. As constantes desses termos são parâmetros ajustados aos dados experimentais.
Suponha o núcleo um elipsóide de revolução com eixo maior dado por
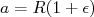 e eixo menor dado por
e eixo menor dado por 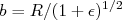 , conforme mostra a figura 2. Nesse caso, assumindo o eixo-z ao longo do eixo maior desse elipsóide, temos que as frequências de oscilação em x e y são iguais, ou seja
, conforme mostra a figura 2. Nesse caso, assumindo o eixo-z ao longo do eixo maior desse elipsóide, temos que as frequências de oscilação em x e y são iguais, ou seja  . Devido à simetria do problema, as frequencias de oscilação são inversamente proporcionais aos comprimentos desses eixos, ou seja:
. Devido à simetria do problema, as frequencias de oscilação são inversamente proporcionais aos comprimentos desses eixos, ou seja:
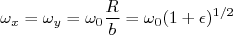 (2)
(2)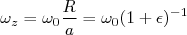 (3)
(3)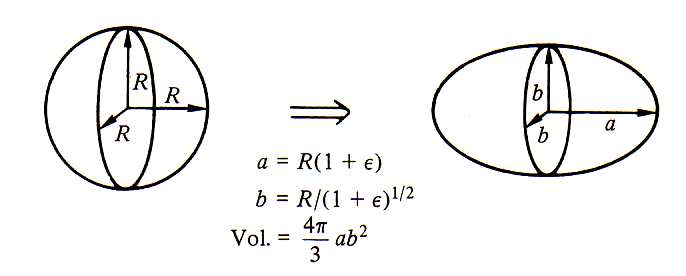
É comum reescrever essas frequências de oscilação em termos de um parâmetro de deformação
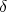 de forma que
de forma que 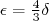 (cuidado! Há muitas parametrizações diferentes para
(cuidado! Há muitas parametrizações diferentes para 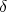 ). Substituindo esse valor em (2) e (3) e fazendo uma expansão em Taylor que resulta em:
). Substituindo esse valor em (2) e (3) e fazendo uma expansão em Taylor que resulta em:
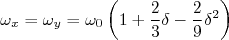 (4)
(4)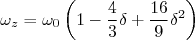 (5)
(5)Essa substituição assegura que
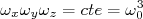 até segunda ordem. Essa condição é necessária para haver conservação do volume nuclear. O parâmetro
até segunda ordem. Essa condição é necessária para haver conservação do volume nuclear. O parâmetro 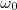 é determinado a partir de medidas de raio médio nuclear (exercício) e vale:
é determinado a partir de medidas de raio médio nuclear (exercício) e vale:
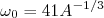 MeV (6)
MeV (6)Dessa forma podemos dizer que, do ponto de vista da forma do potencial do oscilador harmônico há um único parâmetro a ser determinado,
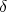 . Assim, uma vez determinadas as constantes do acoplamento spin-órbita e o termo de achatamento do potencial, pode-se determinar os valores de energia para os estados desse potencial em função desse parâmetro de deformação
. Assim, uma vez determinadas as constantes do acoplamento spin-órbita e o termo de achatamento do potencial, pode-se determinar os valores de energia para os estados desse potencial em função desse parâmetro de deformação 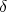 . A comparação desses valores com aqueles medidos experimentalmente determinam a deformação do potencial. Esse cálculo é bastante complexo e não será descrito em detalhes aqui. Valores positivos para
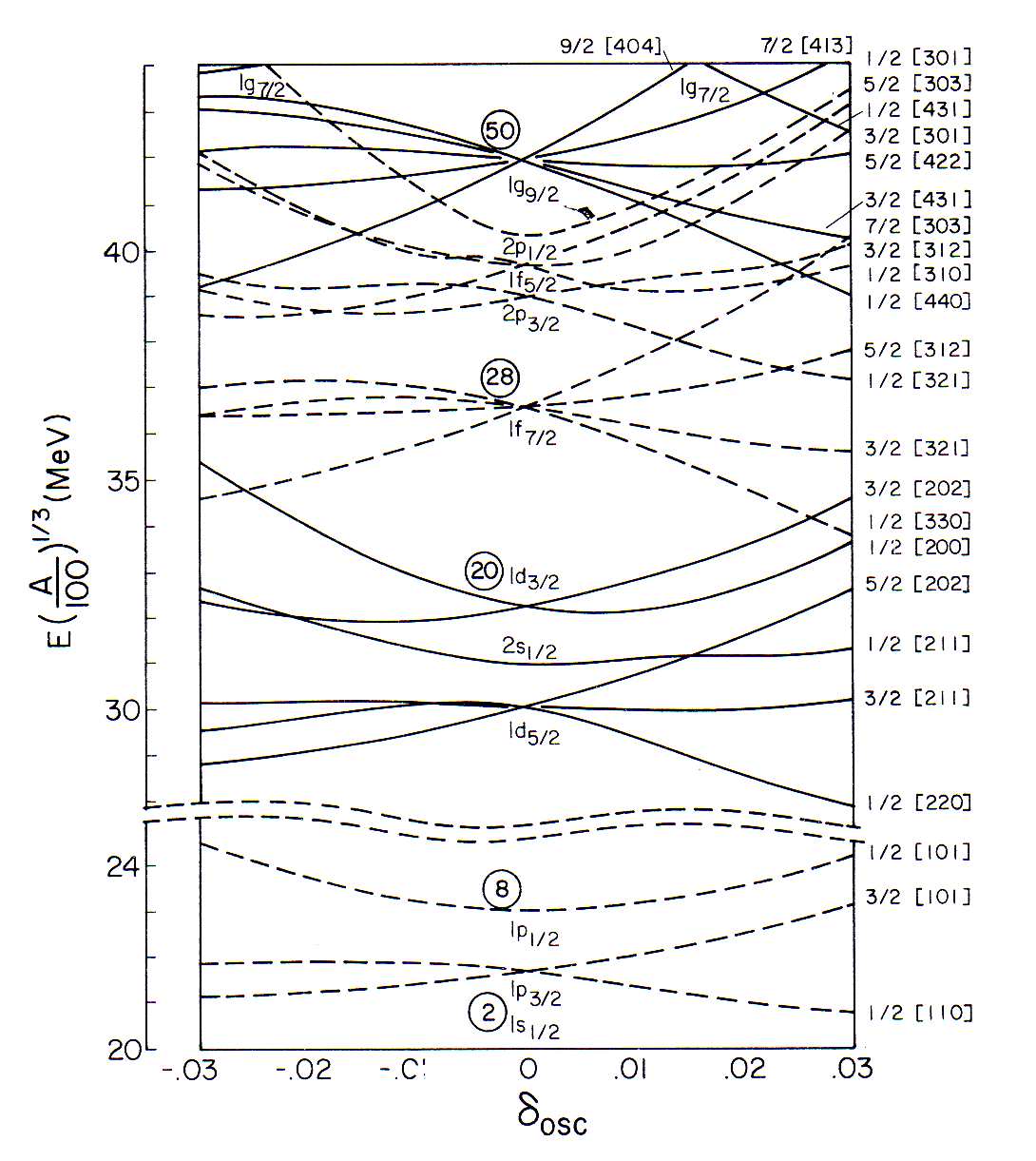
. A comparação desses valores com aqueles medidos experimentalmente determinam a deformação do potencial. Esse cálculo é bastante complexo e não será descrito em detalhes aqui. Valores positivos para 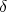 correspondem a um núcleo prolato enquanto valores negativos, oblato. A figura 3 mostra os níveis de energia em função de
correspondem a um núcleo prolato enquanto valores negativos, oblato. A figura 3 mostra os níveis de energia em função de 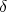 . Note que em um potencial deformado, os momentos angulares
. Note que em um potencial deformado, os momentos angulares 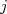 e
e 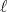 não são bons números quânticos já que essas não são grandezas conservadas. Voltaremos nesse assunto mais a frente quando tratarmos de rotações.
não são bons números quânticos já que essas não são grandezas conservadas. Voltaremos nesse assunto mais a frente quando tratarmos de rotações.
O modelo de Nilsson obteve grande sucesso (em comparação ao modelo de camadas esférico) por ser capaz de explicar, dentre outras grandezas:
- o estado de spin de todos os núcleos leves e quase todos os pesados;
- momentos de dipolo magnético de muitos nucleos (ver figura 4) de forma muito mais acurada que os cáclulos realizados pelas Linhas de Schmidt;
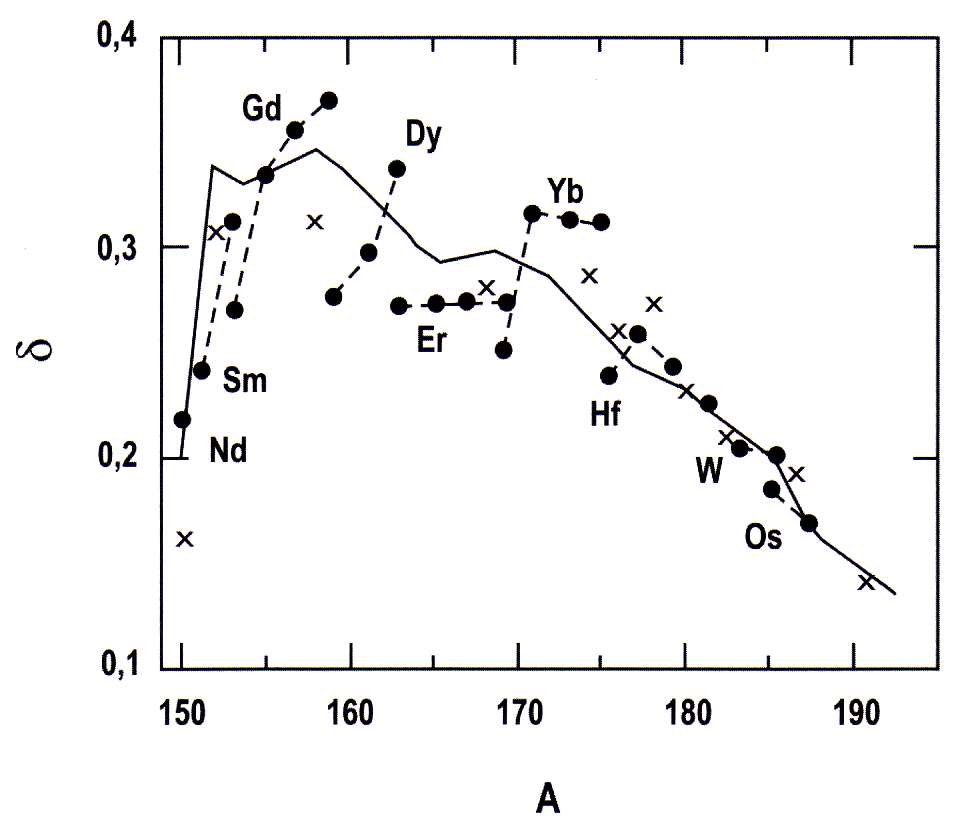
- momentos de quadrupolo elétricos são melhores determinados. Na região de massa entre 150 e 180, por exemplo (ver figura 5), o parâmetro de deformação nuclear é calculado de forma precisa em relação àqueles medidos experimentalmente.

Não poderíamos deixar de notar que a existência de núcleos deformados resulta na possibilidade de existência de rotações coletivas nucleares. Sistemas esfericamente simétricos não são passíveis de rotações. Rotações constituem uma forma peculiar de absorver energia. A absorção de energia por meio de rotações possui características peculiares que podem, dentre outros, revelar informações sobre momentos de inércia do núcleo. Desse modo, o estudo de bandas rotacionais constitui um assunto interessante de ser explorado em física nuclear.
Um esquema de como construiremos um modelo para rotações nucleares encontra-se na figura 6. Definimos o eixo-z como aquele ao longo do eixo de simetria axial do núcleo. Note que, devido a essa simetria, não é possível observar rotações coletivas em torno desse eixo, pois o núcleo é simétrico por rotações em torno de z. Nesse caso, o momento angular devido à rotações coletivas (
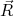 ) deve ser perpendicular a esse eixo. Na figura 6, o vetor
) deve ser perpendicular a esse eixo. Na figura 6, o vetor 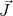 corresponde ao momento angular total intrínseco do núcleo enquanto o vetor
corresponde ao momento angular total intrínseco do núcleo enquanto o vetor 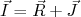 corresponde ao momento angular total, considerando rotações coletivas.
corresponde ao momento angular total, considerando rotações coletivas.
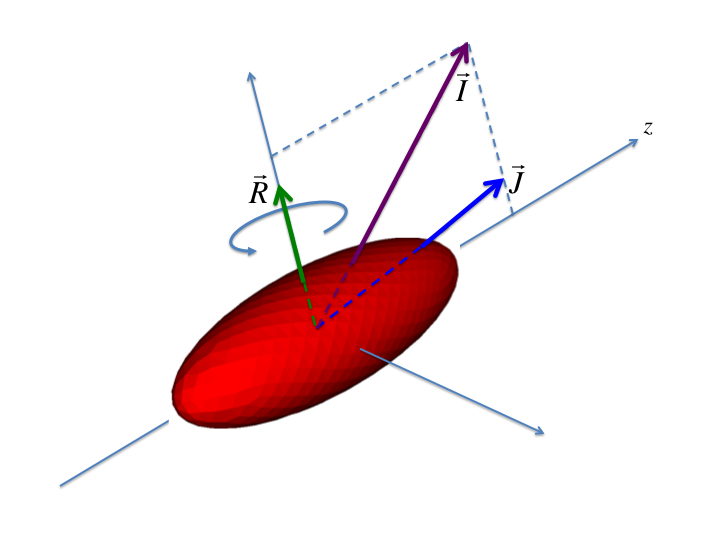
Se as frequências típicas de rotação coletiva do núcleo forem significativamente menores que aquelas devido ao movimento interno dos nucleons, podemos tratar o problema de rotações independente daquele devido à estrutura interna. Nessa situação, a rotação coletiva interfere pouco na função de onda do nucleon e podemos escrever que:
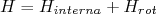 (7)
(7)Nessa situação podemos fazer da função de onda total em uma parte interna e uma parte rotacional. O mesmo se aplica à energia total, ou seja:
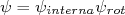 (8)
(8)e
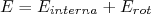 (9)
(9)O Hamiltoniano de rotação do núcleo pode ser escrito de forma análoga à energia de um corpo rígido em rotação, ou seja:
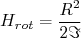 (10)
(10)sendo
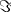 o momento de inércia do núcleo. Como
o momento de inércia do núcleo. Como 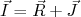 , podemos fazer:
, podemos fazer:
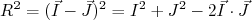 (11)
(11)O produto escalar em (11) pode ser calculado, de modo que:
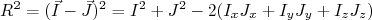 (12)
(12)Lembrando dos operadores de momento angular
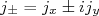 podemos reescrever (12) como:
podemos reescrever (12) como:
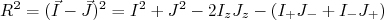 (13)
(13)Também podemos separar o Hamiltoniano de rotação em dois termos, sendo o segundo termo de acoplamento, que vale:
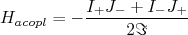 (14)
(14)Esse termo faz um acoplamento entre o momento angular de rotação e o momento angular intrínseco do núcleo. Esse termo corresponde à força de Coriolis no núcleo. Isso cria uma flutuação no momento angular intrínseco do núcleo. Os operadores atuam de forma a mudar em uma unidade o momento angular, aumentando ou diminuindo. Assim, esses operadores interferem em estados cuja projeção do momento angular intrínseco difere apenas de uma unidade. Esse efeito é importante quando essa projeção de momento angular vale
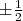 . Vamos, por enquanto, negligenciar esse termo. Nesse caso, o Hamiltoniando de rotação resulta em:
. Vamos, por enquanto, negligenciar esse termo. Nesse caso, o Hamiltoniando de rotação resulta em:
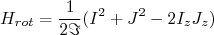 (15)
(15)Como a rotação coletiva do núcleo ocorre perpendicularmente ao eixo-z (ver figura 6), é fácil notar que as componentes em z do momento angular intrínseco (
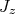 ) e do momento angular total (
) e do momento angular total (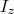 ) são as mesmas. Os autovalores de energia para a parte rotacional do Hamiltoniano nuclear vale, a partir de (15):
) são as mesmas. Os autovalores de energia para a parte rotacional do Hamiltoniano nuclear vale, a partir de (15):
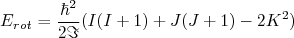 (15)
(15)onde
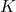 corresponde à projeção do momento angular intrínseco (ou total) no eixo-z. Em (15), como desprezamos possíveis interferências devido à rotação na função de onda interna do núcleo, temos que
corresponde à projeção do momento angular intrínseco (ou total) no eixo-z. Em (15), como desprezamos possíveis interferências devido à rotação na função de onda interna do núcleo, temos que 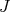 e
e 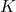 são constantes do movimento. Assim, os níveis de energia de rotação dependem apenas de
são constantes do movimento. Assim, os níveis de energia de rotação dependem apenas de 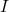 , ou seja, do momento angular de rotação
, ou seja, do momento angular de rotação 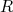 .
.
Podemos voltar agora a uma breve discussão sobre o termo de Coriolis no Hamiltoniano. Em (15), vemos que um autoestado de rotação é degenerado em relação aos auto-estados com projeção
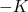 e
e 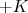 . A força de Coriolis mistura momentos angulares que diferem em
. A força de Coriolis mistura momentos angulares que diferem em  . Para
. Para 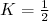 isso é importante pois os estados
isso é importante pois os estados 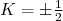 correspondem ao mesmo valor de energia e diferem de uma unidade. Assim, estados rotacionais com
correspondem ao mesmo valor de energia e diferem de uma unidade. Assim, estados rotacionais com 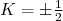 são perturbados por esse acoplamento, alterando os valores dos níveis de energia rotacionais.
são perturbados por esse acoplamento, alterando os valores dos níveis de energia rotacionais.
Rotações nucleares dão orígem a níveis de energia com separação constante entre eles, facilmente de ser calculada a partir de (15). Essa separação está diretamente relacionada ao momento de inércia do núcleo para a banda rotacional investigada. Note que núcleos podem possuir diferentes momentos de inércia. Esses momentos de inércia dependem da orientação do momento angular de rotação e do estado de estrutura interna do núcleo. Além disso, o núcleo possui um comportamento macroscópico similar a uma gota líquida. Desse modo, é natural pensar que elevados momentos angulares de rotação podem provocar deformações nucleares relacionadas à viscosidade da matéria nuclear. Esses estados de elevada rotação podem, portanto, criar estados super-deformados do núcleo. O estudo desses estados super-deformados constitui um campo interessante de pesquisa em Física Nuclear atualmente. Assim, quando falamos em separação constante entre estados de rotação devemos ter o cuidado de pensar em situações nas quais o momento angular de rotação é relativamente baixo.
Vamos explorar duas situações mais simples, que não envolvem o termo de Coriolis. Nesse caso, temos:
- Núcleos par-par - para núcleos par-par, o momento angular intrínseco é nulo, ou seja,
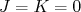 . Nesse caso, os níveis de energia são:
. Nesse caso, os níveis de energia são:
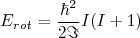 , com
, com 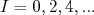 (16)
(16)
O fato de apenas os valores pares de momento angular serem populados não pode ser explicado pelo Hamiltoniando de rotação, que permite qualquer valor inteiro de momento angular. Essa restrição surge da necessidade de respeitar a forma da função de onda total do núcleo, que deve manter simetria no plano x-y. Assim, apenas valores pares de momento angular são observados nesse caso. Na figura 7 vemos um exemplo de bandas rotacionais de dois núcleos par-par deformados.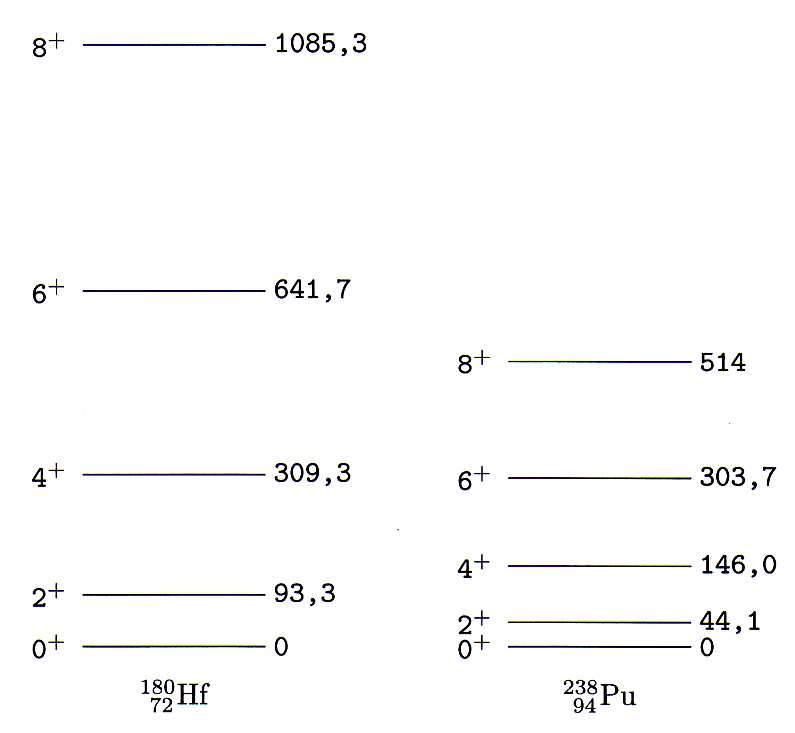
Figura 7 - Exemplo de banda rotacional de núcleos par-par.
- Núcleos ímpares com
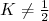 . Nesses casos os níveis de energia são construídos partindo do estado fundamental (sem rotação). Todos os valores de momento angular de rotação são permitidos. Assim, os níveis de energia possuem momento angular dados por
. Nesses casos os níveis de energia são construídos partindo do estado fundamental (sem rotação). Todos os valores de momento angular de rotação são permitidos. Assim, os níveis de energia possuem momento angular dados por 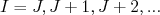 . Um exemplo de uma banda rotacional de um núcleo ímpar pode ser visto na figura 8, para o 175Lu. Na figura 9 vemos o diagrama de níveis de energia para o 239Np. Nesse caso, há duas bandas rotacionais observadas no esquema de níveis, uma construída sobre o estado fundamental
. Um exemplo de uma banda rotacional de um núcleo ímpar pode ser visto na figura 8, para o 175Lu. Na figura 9 vemos o diagrama de níveis de energia para o 239Np. Nesse caso, há duas bandas rotacionais observadas no esquema de níveis, uma construída sobre o estado fundamental  e outra construída sobre o primeiro estado excitado do núcleo que corresponde ao estado
e outra construída sobre o primeiro estado excitado do núcleo que corresponde ao estado  . Os momentos de inércia dessas bandas são diferentes, refletindo as diferenças nas estruturas internas desse núcleo.
. Os momentos de inércia dessas bandas são diferentes, refletindo as diferenças nas estruturas internas desse núcleo.
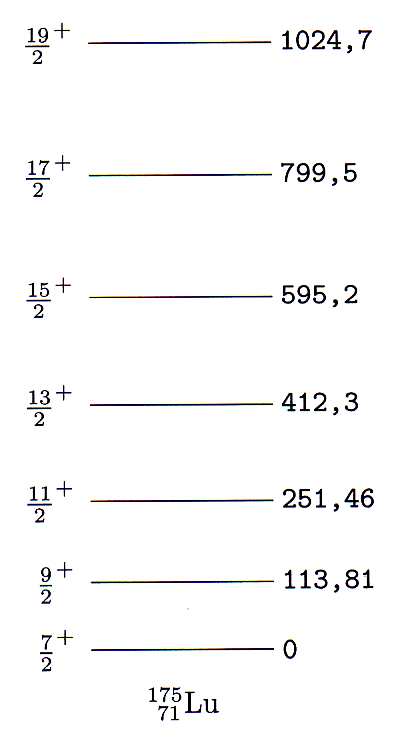
Figura 8 - Exemplo de uma banda rotacional de um núcleo ímpar.

Figura 9 - Núcleo com duas bandas rotacionais.
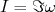 . Tomando:
. Tomando:
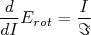 (17)
(17)Faz com que:
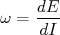 (18)
(18)Experimentalmente podemos determinar a frequência de rotação como a diferença entre dois níveis de energia consecutivos. Lembrando também de substituir o operador I pelo seu auto valor, temos:
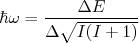 (19)
(19)Para um núcleo par-par, por exemplo:
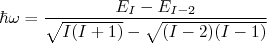 (20)
(20)que, para altos valores de
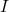 podemos escrever, com boa aproximação:
podemos escrever, com boa aproximação:
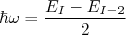 (21)
(21)Por outro lado, pode-se determinar também o momento de inércia do núcleo pela diferença entre a energia de dois níveis consecutivos. A partir de (16) podemos escrever que:
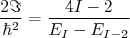 (22)
(22)Se o núcleo fosse um corpo rígido indeformável, um gráfico de momento de inércia em função da frequência de rotação deveria ser uma constante. Pequenos desvios em relação à constante indicariam uma variação do momento de inércia na medida em que o núcleo se deforma devido à sua elevada rotação. O efeito da rotação é de aumentar o momento de inércia. A figura 10 mostra o momento de inércia em função da frequência de rotação para dois núcleos. Para o 174Hf notamos um leve aumento do momento de inércia na medida em que aumentamos a frequência angular, compatível com o esperado. No caso do 158Eu o comportamento observado não é compatível com o esperado. Os números nos pontos experimentais correspondem ao momento angular para cada nível de energia computado. Note que, no caso do 158Eu, o aumento do momento angular, entre 12 e 16, diminui a frequência de rotação.
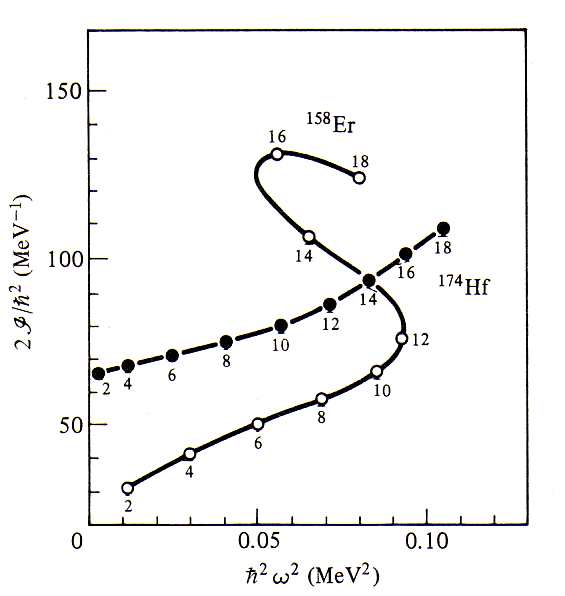
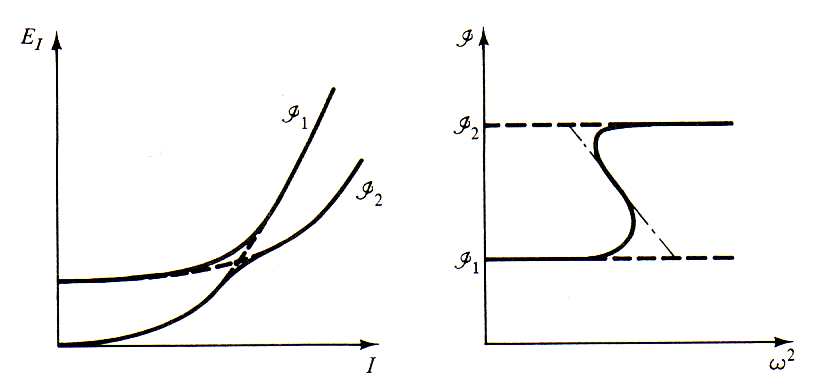
Isso pode ser compreendido a partir da força de Coriolis presente no núcleo, que acopla o momento angular total com o momento angular intrínseco do núcleo. Na medida em que aumentamos o momento angular total, a componente de Coriolis aumenta. Isso gera uma competição entre esse termo e as forças internas de emparelhamento entre nucleons. Em um determinado momento, essa interação pode ser significativamente grande a ponto de romper o emparelhamento interno desses nucleons, levando o núcleo a um estado de excitação interna, rearranjando os nucleons para uma nova configuração de camadas. Nesse caso, há uma mudança drástica do momento de inércia. Um esquema simplificado desse processo é mostrado na figura 11. Esse fenômeno, chamado de backbending, foi observado pela primeira vez por A. Johnson et al. em 1972. Há várias formas de se observar esse comportamento. Por exemplo, na figura 12, vemos um gráfico de momento angular (nesse caso o autor usa o símbolo
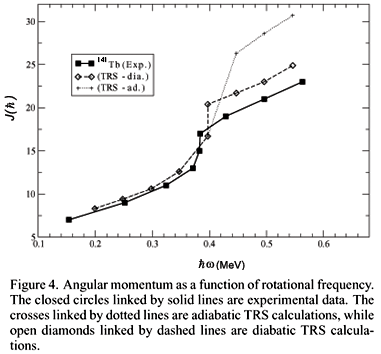
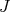 ) em função da frequência de rotação para o núcleo 141Tb. Se o momento angular fosse constante observaríamos uma reta. Nesse caso, nota-se o desvio do comportamento linear e, próximo ao momento angular
) em função da frequência de rotação para o núcleo 141Tb. Se o momento angular fosse constante observaríamos uma reta. Nesse caso, nota-se o desvio do comportamento linear e, próximo ao momento angular 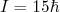 vemos uma mudança busca, compatível com backbending.
vemos uma mudança busca, compatível com backbending.
O fenômeno de backbending é bastante observado na natureza. Em alguns núcleos, como o 160Yb nota-se, inclusive, um segundo backbending. Hoje em dia se conhece um número enorme de bandas de rotação nucleares. Muitas dessas bandas são caracterizadas por estados superdeformados do núcleo, alguns com razão entre eixo maior e menor de aproximadamente 2:1. Esse é um campo extremamente ativo de pesquisa.
A estrutura do núcleo é muito complexa, por ser um sistema fortemente interagente de muitos corpos. A complexidade das interações binárias tornam os observaveis nucleares muito sensíveis à estrutura desses núcleos. Discutimos diversos modelos nucleares, desde modelos de partícula independente, como o modelo de camadas e variações/correções nesses modelos, como o acoplamento spin-órbita, correções de interações de dois corpos, emparelhamento, etc. Vimos também como comportamentos coletivos nucleares podem influenciar a estrutura interna. Por exemplo, o modelo de Nilsson para um potencial deformado. Isso sugere a existência de estados coletivos de rotações. Essas rotações geram efeitos interessantes na estrutura nuclear, como deformações dinâmicas e backbending. Vários outros efeitos foram deixados de lado, como efeitos vibracionais nucleares, por exemplo. Essa complexidade mantém a o estudo da estrutura nuclear como um dos grandes tópicos de pesquisa atual em física nuclear.
Exercícios
- Mostre (6). Dica: ver apêndice B de "Introdução à Física Nuclear", H. Schechter e C. A. Bertulani.
- O momento de quadrupolo magnético do 177Lu é 3.33 barns e seu momento angular é
 . Usando o modelo de Nilsson, calcule o parâmetro de deformação
. Usando o modelo de Nilsson, calcule o parâmetro de deformação 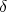 para esse núcleo.
para esse núcleo.
- A partir dos dados da figura 8, obtenha o gráfico do momento de inércia em função da frequência de oscilação (similar à figura 10). O momento de inércia desse núcleo pode ser considerado constante? Discuta.
- Repita o exercício anterior para as duas bandas mostradas na figura 9. Compare os dois momentos de inércia.
Leitura recomendada
- Introductory Nuclear Physics, K. S. Krane, capítulo 5.
- Fundamentals of nuclear physics, N. A. Jelley, capítulo 2.
- Introdução à Física Nuclear, H. Schechter e C. A. Bertulani, capítulos 4.




No comments