Modelo de camadas - spin-órbita
Notas de aula são propriedade intelectual. Sendo assim, qualquer uso, no todo ou em parte, deve ter a origem referenciada apropriadamente, após autorização de seu autor.
O texto a seguir corresponde à anotações parciais de aula. Não é um texto em forma final, completo e totalmente revisado. Nesse caso, esse texto não tem como objetivo substituir livros sobre o assunto. Assim, esse texto deve ser entendido apenas como um guia de estudo para o aluno acompanhar a disciplina.
Em 1949 Maria G. Mayer e Hans Jensen introduziram a idéia de acoplamento spin-órbita no modelo de camadas nuclear. Até então, potenciais radiais não eram capazes de descrever os números mágicos observados nem a estrutura de níveis de energia. Ao contrário de outros vários termos no potencial de interação nucleon-nucleon, discutido anteriormente, não há razão aparente para esse termo possuir efeito médio pequeno e, portanto, ser tratado como uma interação residual. Dessa forma, devemos alterar o potencial de interação central e adicionar um termo de acoplamento, resultando em:
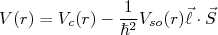 (1)
(1)O termo
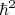 simplifica a comparação entre o potencial
simplifica a comparação entre o potencial 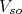 e o termo central
e o termo central 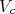 . Como já vimos anteriormente, adicionar o termo de spin-órbita no Hamiltoniano do sistema faz com que as projeções de momento angular orbital e spin não sejam mais constantes de movimento e, para recuperar esses dois números quânticos perdidos criamos o conceito de momento angular total (
. Como já vimos anteriormente, adicionar o termo de spin-órbita no Hamiltoniano do sistema faz com que as projeções de momento angular orbital e spin não sejam mais constantes de movimento e, para recuperar esses dois números quânticos perdidos criamos o conceito de momento angular total (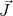 ) e sua projeção. Como o spin do nucleon vale 1/2, o momento angular total pode assumir dois valores, na soma vetorial:
) e sua projeção. Como o spin do nucleon vale 1/2, o momento angular total pode assumir dois valores, na soma vetorial: 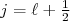 ou
ou 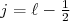 , ou seja, o acoplamento de momento angular e spin deve separar os níveis de energia em dois estados distintos, cada um com um valor de momento angular total.
, ou seja, o acoplamento de momento angular e spin deve separar os níveis de energia em dois estados distintos, cada um com um valor de momento angular total.
O momento angular total é dado, como sabemos, por:
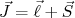 (2)
(2)Assim, podemos escrever que:
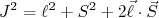 (3)
(3)de modo que:
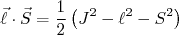 (4)
(4)O potencial dado em (1) torna-se:
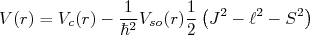 (5)
(5)Vamos calcular como o acoplamento spin-órbita separa os estados de energia. Para isso, vamos calcular o valor médio do termo de spin-órbita do potencial. Assumindo que os auto-estados não sofrem alteração substanciais, podemos escrever que a variação em energia de um determinado nível corresponde ao valor médio desse termo. Primeiramente, vamos obter o valor médio de
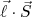 , que vale:
, que vale:
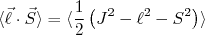 (6)
(6)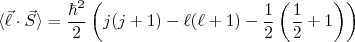 (7)
(7)Que resulta, para
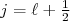 :
:
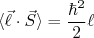 (8)
(8)e, para
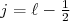 :
:
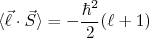 (9)
(9)Desse modo, podemos calcular o valor médio do potencial spin-órbita, que corresponde ao deslocamento em energia, como sendo:
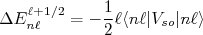 (10)
(10)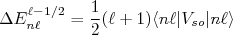 (11)
(11)Assim, a separação entre os níveis de energia pode ser dada pela diferença entre os dois termos acima, ou seja:
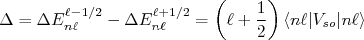 (12)
(12)A amplitude da separação depende de cada nível de energia no núcleo. Contudo, podemos ver que, quanto maior o momento angular orbital do nível, maior é essa separação. Isso é razoável de pensar, uma vez que a amplitude do acoplamento depende explicitamente da amplitude do momento angular orbital e o spin do nucleon ter sempre valor 1/2. Essa dependência do momento angular orbital na magnitude da separação entre os níveis de energia causa efeitos interessantes no ordenamento de níveis nucleares. Em alguns casos a separação é tão grande que o novo estado cruza com outros, invertendo a ordem na qual os níveis de energia são populados.
A figura 1 mostra o efeito de separação de níveis de energia em um potencial de Wood-Saxon com o acoplamento spin-órbita. Note que o potencial com o acoplamento spin-orbita consegue, finalmente, reproduzir todos os números mágicos observados no núcleo atômico.
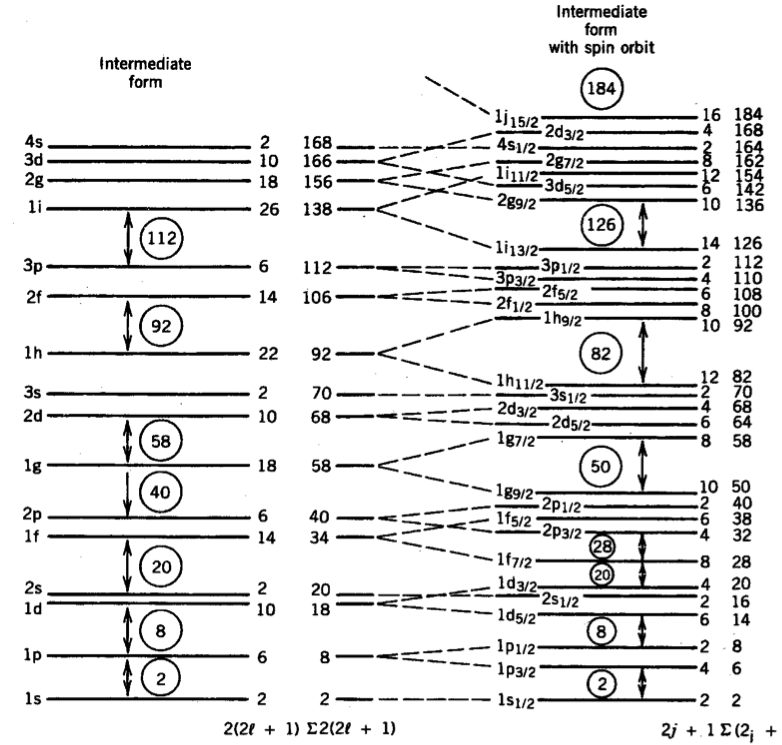
Similar ao modelo atômico, podemos utilizar esse esquema de níveis de energia para extrair propriedades nucleares. Como no modelo atômico, cada nível de energia é caracterizado por um número quântico principal, momento angular orbital e total. Cada nível comporta
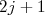 nucleons do mesmo tipo (prótons ou nêutrons). Os nucleons vão sendo distribuídos, começando pelo nível menos energético, respeitando o princípio de exclusão de Pauli. Esse modelo, também denominado de Modelo da camadas extremo ou Modelo de partícula única supõe que não há interações residuais, ou seja, um nucleon em uma camada não afeta a distribuição dos níveis de energia. Como consequência desse modelo, um núcleo par-par possui um caroço inerte, de momento angular total nulo e um núcleo ímpar possui momento angular e paridade dados pelo estado no qual se encontra o nucleon desemparelhado. Nós já utilizamos essa hipótese várias vezes para descrever propriedades macroscópias do núcleo e agora justificamos a sua origem.
nucleons do mesmo tipo (prótons ou nêutrons). Os nucleons vão sendo distribuídos, começando pelo nível menos energético, respeitando o princípio de exclusão de Pauli. Esse modelo, também denominado de Modelo da camadas extremo ou Modelo de partícula única supõe que não há interações residuais, ou seja, um nucleon em uma camada não afeta a distribuição dos níveis de energia. Como consequência desse modelo, um núcleo par-par possui um caroço inerte, de momento angular total nulo e um núcleo ímpar possui momento angular e paridade dados pelo estado no qual se encontra o nucleon desemparelhado. Nós já utilizamos essa hipótese várias vezes para descrever propriedades macroscópias do núcleo e agora justificamos a sua origem.
Tomemos como exemplo os núcleos 13C e 13N. Ambos os núcleos possuem um nucleon desemparelhado. Um nêutron, no primeiro caso, e um próton, no segundo. Os 12 primeiros nucleons (6 prótons e 6 nêutrons) se acoplam com modelo angular total nulo. Segundo o esquema de níveis de energia na figura 1, o nucleon desemparelhado ocuparia o estado
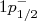 , indicando que esses núcleos possuem momento angular total 1/2 e momento angular orbital 1. De fato observa-se isso experimentalmente. O mesmo ocorre, por exemplo, com os núcleos de 17F e 17O, que possuem estado
, indicando que esses núcleos possuem momento angular total 1/2 e momento angular orbital 1. De fato observa-se isso experimentalmente. O mesmo ocorre, por exemplo, com os núcleos de 17F e 17O, que possuem estado 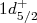 . Outros exemplos são o 15O e 15N. Nesse caso, temos um nucleon faltando para preencher um nível. O estado previsto pelo modelo
. Outros exemplos são o 15O e 15N. Nesse caso, temos um nucleon faltando para preencher um nível. O estado previsto pelo modelo 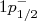 concorda com medidas experimentais.
concorda com medidas experimentais.
No caso de núcleos ímpar-ímpar a situação é um pouco mais complexa. Nesse caso temos um próton e um nêutron desemparelhado. Segundo o modelo de camadas extremo, sendo
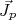 e
e 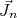 os momentos angulares do próton e nêutron, respectivamente, o momento angular total do núcleo corresponde à soma desses momentos angulares orbitais. Assim, o núcleo pode ter momento angular total entre
os momentos angulares do próton e nêutron, respectivamente, o momento angular total do núcleo corresponde à soma desses momentos angulares orbitais. Assim, o núcleo pode ter momento angular total entre 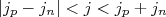 . Em 1950, L. W. Nordheim propôs algumas regras que permitiriam determinar qual seria o acoplamento mais provável em núcleos ímpar-ímpar. Define-se o número de Nordheim como sendo:
. Em 1950, L. W. Nordheim propôs algumas regras que permitiriam determinar qual seria o acoplamento mais provável em núcleos ímpar-ímpar. Define-se o número de Nordheim como sendo:
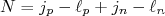 (13)
(13)Há duas regras definidas por Nordheim:
- Regra forte: Se
 , então
, então 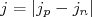 .
.
- Regra fraca: Se
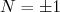 , então
, então 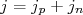 ou
ou 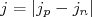 .
.
 , assim o momento angular previsto seria 2 (o próton encontra-se no estado 3/2 e o nêutron no 7/2). De fato, o momento angular observado é o estado
, assim o momento angular previsto seria 2 (o próton encontra-se no estado 3/2 e o nêutron no 7/2). De fato, o momento angular observado é o estado 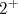 . No caso do 14N, o número de Nordheim vale
. No caso do 14N, o número de Nordheim vale 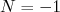 , indicando que o momento angular previsto seria 0 ou 1. O observado é
, indicando que o momento angular previsto seria 0 ou 1. O observado é  .
.
O modelo de camadas extremo funciona bem quando temos apenas 1 nucleon acima de um nível totalmente preenchido, ou um nucleon faltando para preencher totalmente um determinado nível. Ele não funciona muito bem em algumas circunstâncias nas quais temos mais que um nucleon em um nível não fechado ou em sistemas que possuem coletividade muito elevada (já vimos isso em momentos de quadrupolo elétrico para núcleos terras raras). Por exemplo, o 47Ti deveria ter nucleons preenchendo os níveis de energia até o estado
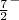 . Contudo, medidas experimentais indicam que o estado fundamental desse núcleo é o
. Contudo, medidas experimentais indicam que o estado fundamental desse núcleo é o  . Isso pode ser atribuído a interações entre duas partículas residuais que resultam em diferentes acoplamentos de momento angulares nesses níveis não totalmente preenchidos. Mesmo em situações nas quais temos apenas um nuclídio desemparelhado, como no 203Tl, pode haver pequenas interações residuais que alteram levemente o acoplamento de momentos angulares. Nesse caso, segundo o modelo de camadas extremo, o estado fundamental do núcleo deveria ser o
. Isso pode ser atribuído a interações entre duas partículas residuais que resultam em diferentes acoplamentos de momento angulares nesses níveis não totalmente preenchidos. Mesmo em situações nas quais temos apenas um nuclídio desemparelhado, como no 203Tl, pode haver pequenas interações residuais que alteram levemente o acoplamento de momentos angulares. Nesse caso, segundo o modelo de camadas extremo, o estado fundamental do núcleo deveria ser o 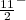 e, contudo, observa-se o estado
e, contudo, observa-se o estado 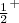 .
.
O primeiro pensamento que surge é devido à aproximação efetuada para criar o modelo de camandas. Nesse modelo, substituímos as interações de dois corpos por um potencial efetivo e supomos que a diferença entre esse potencial efetivo e o real poderia ser tratada como uma interação residual. Nesse caso, nucleons que se encontram em níveis parcialmente cheios deveminteragir binariamente. Essa interação residual pode quebrar a degenerescência em energia desses níveis, separando os estados em novas energias e momentos angulares. Nesses casos, os níveis de energia apresentados na figura 1 teriam seu esquema modificados. Vamos discutir isso a seguir.
Exercícios
- Considere os níveis de energia da figura 1. Assumindo uma escala qualquer em energia, calcule o valor de
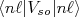 em função de
em função de 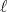 . Discuta de a dependência obtida a partir desses resultados são compatíveis com o esperado para o potencial de spin-orbita.
. Discuta de a dependência obtida a partir desses resultados são compatíveis com o esperado para o potencial de spin-orbita.
- Repita o segundo exercício da última aula, porém usando os níveis de energia após a correção para o acoplamento spin-órbita, ou seja, preveja os valores possíveis de
 dos estados fundamentais dos núcleos: 27Mg e 87Sr. Compare com os valores observados
dos estados fundamentais dos núcleos: 27Mg e 87Sr. Compare com os valores observados 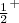 e
e 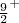 . Compare com os resultados obtidos na aula anterior. Discuta as eventuais diferenças.
. Compare com os resultados obtidos na aula anterior. Discuta as eventuais diferenças.
Leitura recomendada
- Maria Mayer - Nobel Prize lecture
- L. W. Nordhein, beta decay and the nuclear shell model, 1950
- Introductory Nuclear Physics, K. S. Krane, capítulo 5.
- Introduction to Nuclear and Particle Physics, A. Das e T. Ferbel, capítulo 3.
- Introdução à Física Nuclear, H. Schechter e C. A. Bertulani, capítulos 4.
- Nuclear and Prticle Physics, W. S. C. Williams, capítulo 8.




No comments