Modelo de camadas - alguns potenciais
Notas de aula são propriedade intelectual. Sendo assim, qualquer uso, no todo ou em parte, deve ter a origem referenciada apropriadamente, após autorização de seu autor.
O texto a seguir corresponde à anotações parciais de aula. Não é um texto em forma final, completo e totalmente revisado. Nesse caso, esse texto não tem como objetivo substituir livros sobre o assunto. Assim, esse texto deve ser entendido apenas como um guia de estudo para o aluno acompanhar a disciplina.
Vamos considerar alguns potenciais radiais simples para tentar obter o espectro de níveis de energia de um núcleo atômico. O potencial mais simples que podemos utilizar é o poço quadrado infinito. Esse poço é por demais simplificado. Podemos pensar, por exemplo, que o poço infinito não permite escape de nucleons do núcleo, impedindo, por exemplo, decaimento nuclear por partículas α. Na verdade, deveríamos começar com o poço retangular finito. Contudo, para
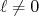 as soluções são apenas numéricas. A diferença principal entre o poço finito e infinito surge nas condições de contorno. Enquanto que, para o poço infinito, a função de onda deve assumir o valor zero na borda do poço, no finito há uma pequena penetração além da sua fronteira. Essa pequena diferença altera levemente a distribuição de níveis de energia, principalmente em níveis próximos da energia zero. Contudo, qualitativamente, os resultados obtidos com o poço infinito permitem exemplificar de forma satisfatória algumas características observadas no núcleo.
as soluções são apenas numéricas. A diferença principal entre o poço finito e infinito surge nas condições de contorno. Enquanto que, para o poço infinito, a função de onda deve assumir o valor zero na borda do poço, no finito há uma pequena penetração além da sua fronteira. Essa pequena diferença altera levemente a distribuição de níveis de energia, principalmente em níveis próximos da energia zero. Contudo, qualitativamente, os resultados obtidos com o poço infinito permitem exemplificar de forma satisfatória algumas características observadas no núcleo.
Seja então um poço infinito de largura radial
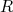 . Acima desse valor o potencial é infinito enquanto que, abaixo desse valor, o potencial é nulo. Isso é muito similar ao modelo de gás de Fermi. Contudo, nessa situação, trataremos o problema com a simetria esférica apropriada, de onde surgirá a dependência dos níveis de energia com o momento angular orbital correspondente.
. Acima desse valor o potencial é infinito enquanto que, abaixo desse valor, o potencial é nulo. Isso é muito similar ao modelo de gás de Fermi. Contudo, nessa situação, trataremos o problema com a simetria esférica apropriada, de onde surgirá a dependência dos níveis de energia com o momento angular orbital correspondente.
A equação para a parte radial da função de onda para esse potencial, no interior do poço, pode ser escrita como:
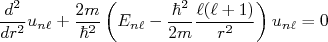 (1)
(1)As soluções de (1) são proporcionais às funções de Bessel esféricas:
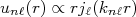 (2)
(2)onde:
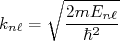 (3)
(3)A quantização de energia, nesse caso, surge da aplicação das condições de contorno em
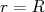 , o raio do potencial. Nesse caso,
, o raio do potencial. Nesse caso, 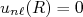 . Assim, temos que, para cada valor de
. Assim, temos que, para cada valor de 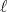 devemos respeitar que:
devemos respeitar que:
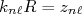 (4)
(4)onde
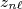 corresponde ao n-ésimo zero da função de Bessel esférica de órdem
corresponde ao n-ésimo zero da função de Bessel esférica de órdem 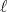 .
A tabela 1 mostra os primeiros zeros de funções de Bessel esféricas para vários valores de momento angular orbital.
.
A tabela 1 mostra os primeiros zeros de funções de Bessel esféricas para vários valores de momento angular orbital.
 |
 |
 |
 |
|
 |
3.142 | 6.283 | 9.425 | 12.566 |
 |
4.493 | 7.725 | 10.904 | 14.066 |
 |
5.763 | 9.095 | 12.323 | 15.515 |
 |
6.988 | 10.417 | 13.698 | 16.924 |
 |
8.183 | 11.705 | 15.040 | 18.301 |
Substituindo (3) em (4), chegamos, finalmente à:
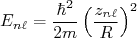 (5)
(5)A figura 1 mostra o esquema de níveis de energia obtidos com o poço quadrado infinito. Do lado esquerdo é mostrado o n-ésimo zero e momento angular correspondentes àquele nível. Do lado direito é mostrado o número de prótons (ou nêutrons) que poderiam ocupar esse nível, dado por
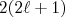 , sendo o primeiro fator 2 devido à degenerescência de spin. Note que, nesse modelo, não há degenerescência de estados senão aquelas devido à projeção de spin e momento angular orbital, ou seja, não há níveis de mesma energia e
, sendo o primeiro fator 2 devido à degenerescência de spin. Note que, nesse modelo, não há degenerescência de estados senão aquelas devido à projeção de spin e momento angular orbital, ou seja, não há níveis de mesma energia e 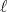 diferentes, por exemplo.
diferentes, por exemplo.
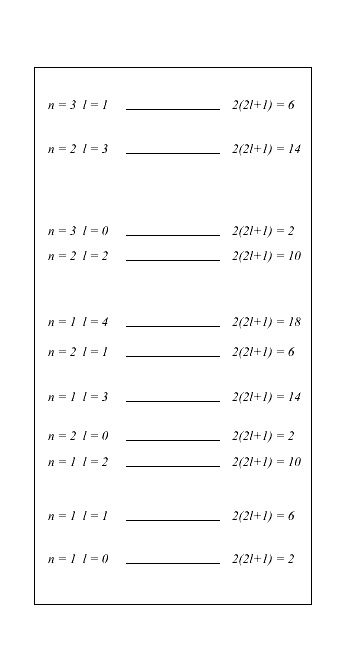
Os números mágicos podem ser calculados considerando, por exemplo, quando há duas camadas relativamente distantes se comparada às demais. Na figura 1 podemos dizer que isso ocorre entre as camadas 1-2, 2-3, 4-5, 5-6, 7-8, etc. resultando nos seguintes números mágicos:
- 2
- 2 + 6 = 8
- 8 + 10 + 2 = 20
- 20 + 14 = 34
- 34 + 6 + 18 = 58, etc.
Uma segunda opção para o potencial de interação, também simples e com resolução analítica, é o potencial de oscilador harmônico radial, ou seja, aquele no qual o potencial é dado por:
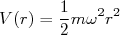 (6)
(6)Assim, a equação radial torna-se:
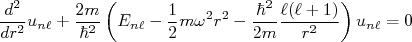 (7)
(7)A resolução de (7) não vem ao caso nesse momento. A componente radial dos autoestados para esse potencial possui uma forma complexa, composta de exponenciais decrescrentes (que limitam a penetração da função de onda para o interior da barreira de potencial) e polinômios de Laguerre, na forma:
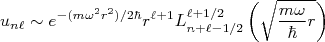 (8)
(8)Os autovalores, contudo, assumem uma forma simplificada, similar ao oscilador harmônico simples:
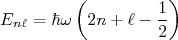 (9)
(9)Sendo
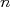 e
e 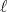 números inteiros positivos, pode-se notar que pode haver diferentes combinações de
números inteiros positivos, pode-se notar que pode haver diferentes combinações de 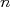 e
e 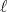 que resultam no mesmo nível de energia. Desse modo, o potencial de oscilador harmônico possui níveis de energia degenerados nesses dois números quânticos. Vamos tentar calcular essa degenerescência de modo a obter os números mágicos fornecidos por esse potencial.
que resultam no mesmo nível de energia. Desse modo, o potencial de oscilador harmônico possui níveis de energia degenerados nesses dois números quânticos. Vamos tentar calcular essa degenerescência de modo a obter os números mágicos fornecidos por esse potencial.
Primeiramente, para simplificar, vamos fazer uma mudança de variável:
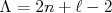 (10)
(10)que, substituindo em (9), resulta em:
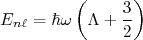 (11)
(11)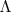 pode, segundo (10), assumir qualquer valor inteiro maior ou igual a zero. Nota-se, assim, que o nível de energia mais baixo para o oscilador harmônico, como esperado, não possui energia nula. Precisamos agora contar quantas combinações de
pode, segundo (10), assumir qualquer valor inteiro maior ou igual a zero. Nota-se, assim, que o nível de energia mais baixo para o oscilador harmônico, como esperado, não possui energia nula. Precisamos agora contar quantas combinações de 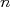 e
e 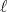 podemos construir para cada estado
podemos construir para cada estado 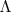 . Devemos dividir essa contagem em duas categorias:
. Devemos dividir essa contagem em duas categorias: 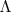 (ou
(ou 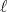 ) sendo par ou
) sendo par ou 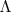 (ou
(ou 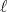 ) sendo ímpar. Para
) sendo ímpar. Para 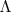 par podemos escrever:
par podemos escrever:
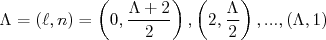 (12)
(12)Para
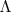 ímpar:
ímpar:
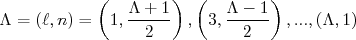 (13)
(13)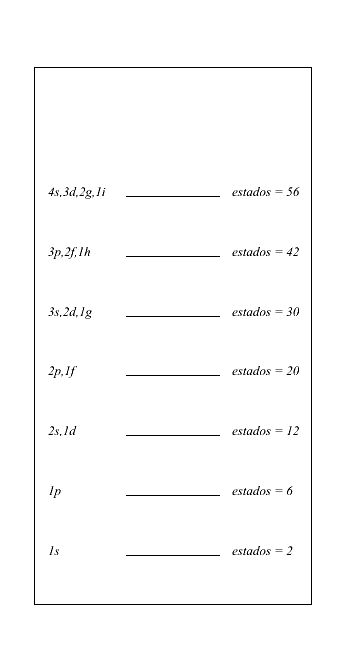
Pode-se notar, também, que a degenerescência em energia não mistura estados de paridade diferente. Cada estado possui paridade bem definida. Na figura 2 podemos ver os níveis de energia de um oscilador harmônico radial. Nesse caso, os números mágicos, como não há nenhuma concentração evidente de níveis, são:
- 2
- 2 + 6 = 8
- 8 + 12 = 20
- 20 + 20 = 40
- 40 + 30 = 70, etc.
Uma forma intermediária é o potencial de Woods-Saxon (figura 3). Esse potencial é dado pela expressão:
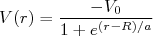 (14)
(14)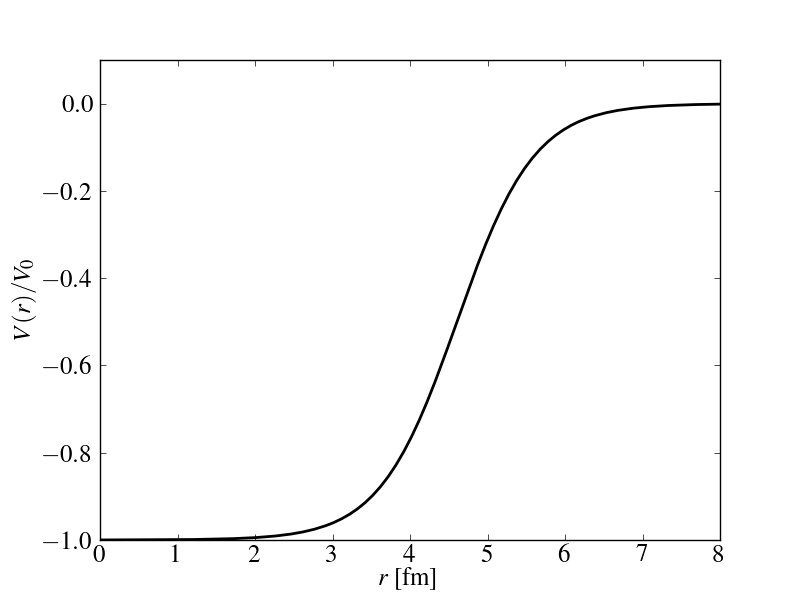
Além de ser uma forma intermediária entre o poço quadrado e o oscilador harmônico, o potencial de Woods-Saxon representa também a distribuição de carga e massa nuclear, como vimos anteriormente. A troca de sinal se dá apenas por conta da força nuclear ser atrativa. Como a interação nucleon-nucleon é de curto alcance, esse potencial se torna bastante interessante na descrição da interação média entre os nucleons no núcleo. Contudo, encontrar os nívies de energia e auto-estados desse potencial não é uma tarefa simples. Normalmente utilizam-se procedimentos numéricos diversos para resolver esse potencial. A figura 4 mostra os níveis de energia obtidos com um potencial de Woods-Saxon, como o mostrado na figura 3.
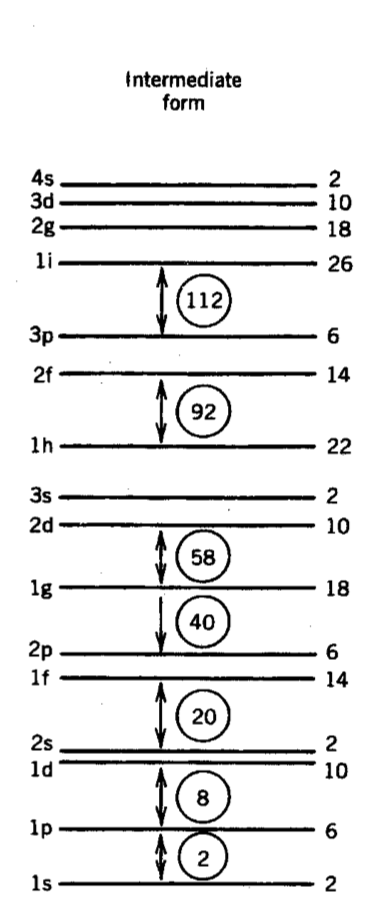
Os números mágicos obtidos com esse potencial são:
- 2
- 2 + 6 = 8
- 8 + 10 + 2 = 20
- 20 + 14 + 6 = 40
- 40 + 18 = 58, etc.
Os valores na tabela 2 indicam claramente que os potenciais utilizados para descrever a interação média dos nucleons no núcleo não são capazes de reproduzir os números mágicos observados. Quase duas décadas depois, nos anos de 1940-1950 era claro que potenciais puramente centrais não eram capazes de reproduzir esses números mágicos. Uma mudança crucial ocorreu em 1949 com o surgimento de correções devido a interações spin-órbita. Veremos isso a seguir.
Exercícios
- As energias de ligação dos núcleos 15O, 16O e 17O são, respectivamente, 111.95 MeV, 127.62 MeV e 131.76 MeV. Deduza as energias do último estado ocupado e do primeiro estado não ocupado do 16O.
- Usando os potenciais discutidos aqui, preveja os valores possíveis de
 dos estados fundamentais dos núcleos: 27Mg e 87Sr. Compare com os valores observados
dos estados fundamentais dos núcleos: 27Mg e 87Sr. Compare com os valores observados 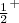 e
e 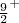
Leitura recomendada
- Introductory Nuclear Physics, K. S. Krane, capítulo 5.
- Introduction to Nuclear and Particle Physics, A. Das e T. Ferbel, capítulo 3.
- Introdução à Física Nuclear, H. Schechter e C. A. Bertulani, capítulos 4.4.
- Nuclear and Prticle Physics, W. S. C. Williams, capítulo 8.




No comments