Núcleos complexos - o modelo de Fermi
Notas de aula são propriedade intelectual. Sendo assim, qualquer uso, no todo ou em parte, deve ter a origem referenciada apropriadamente, após autorização de seu autor.
O texto a seguir corresponde à anotações parciais de aula. Não é um texto em forma final, completo e totalmente revisado. Nesse caso, esse texto não tem como objetivo substituir livros sobre o assunto. Assim, esse texto deve ser entendido apenas como um guia de estudo para o aluno acompanhar a disciplina.
O modelo mais simples para descrever um núcleo complexo é o modelo de gás de Fermi. Nesse modelo supõe-se que nucleons (férmions) possam se movimentar livremente em uma região confinada do espaço, que define o núcleo. Os níveis de energia ocupados por essas partículas são definidos pelo confinamento dessas partículas nessa região e o número de partículas que podem ocupar cada nível é dado pelo princípio de exclusão de Pauli. A contagem do número de partículas que preenchem cada nível de energia permite extrair algumas características macroscópicas do núcleo.
O modelo de gás de Fermi pode ser construído a partir de um modelo simples de partículas "livres", não interagentes, confinadas em uma caixa cúbica de volume
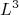 . No interior da caixa, devemos resolver a Equação de Schrödinger para cada partícula, individualmente e na ausência de potencial, ou seja:
. No interior da caixa, devemos resolver a Equação de Schrödinger para cada partícula, individualmente e na ausência de potencial, ou seja:
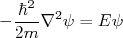 (1)
(1)Em uma caixa cúbica, podemos escrever a função de onda dessa como o produto de funções de onda nos eixos x, y e z, ou seja:
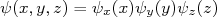 (2)
(2)onde (expressões análogas para as outras coordenadas):
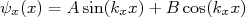 (3)
(3)Tomando um vértice da caixa na origem do sistema de coordenadas e sabendo que a partícula está confinada, temos que
 . Para satisfazer a condição de confinamento precisamos também anular a função de onda em
. Para satisfazer a condição de confinamento precisamos também anular a função de onda em  . Assim, temos que:
. Assim, temos que:
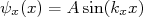 com
com 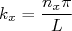 (4)
(4)sendo
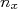 um número inteiro. De (1) podemos relacionar o módulo de
um número inteiro. De (1) podemos relacionar o módulo de 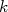 com a energia da partícula através de:
com a energia da partícula através de:
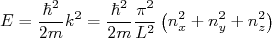 (5)
(5)Note que, em (5), há uma degenerescência na energia, pois é possível fazer várias combinações de números de onda que resultam na mesma energia. Contudo, para um estado bem definido,
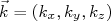 só podemos encontrar 4 partículas, dois prótons, com projeções de spin diferentes, e dois nêutrons, também com projeções de spin diferentes.
só podemos encontrar 4 partículas, dois prótons, com projeções de spin diferentes, e dois nêutrons, também com projeções de spin diferentes.
Para um núcleo com
 prótons e
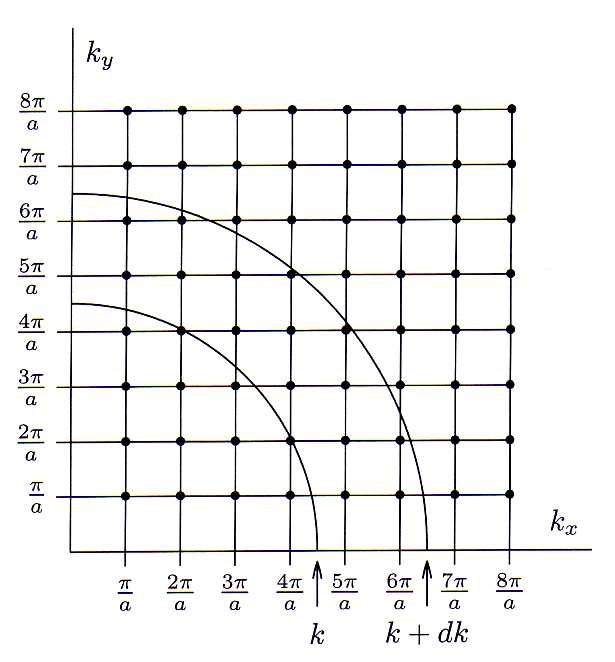
prótons e 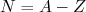 nêutrons, devemos ser capazes de estabelecer quais níveis de energia são populados pelos nucleons. Para isso, precisamos calcular a densidade de níveis de energia presentes no gás, ou seja, calcular quantos estados quânticos temos disponíveis para um determinado estado de energia. A figura 1 mostra os estados possíveis de serem populados no plano
nêutrons, devemos ser capazes de estabelecer quais níveis de energia são populados pelos nucleons. Para isso, precisamos calcular a densidade de níveis de energia presentes no gás, ou seja, calcular quantos estados quânticos temos disponíveis para um determinado estado de energia. A figura 1 mostra os estados possíveis de serem populados no plano  . O número de estados em um intervalo entre
. O número de estados em um intervalo entre 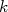 e
e 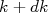 consiste no volume dessa casca esférica dividido pelo volume no espaço de fase ocupado por um único estado. Pode-se ver que cada estado ocupa um volume dado por
consiste no volume dessa casca esférica dividido pelo volume no espaço de fase ocupado por um único estado. Pode-se ver que cada estado ocupa um volume dado por 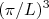 (no desenho da figura 1, usa-se outra variável para designar a largura da caixa e temo que
(no desenho da figura 1, usa-se outra variável para designar a largura da caixa e temo que  ). Assim, o número de estados no intervalo entre
). Assim, o número de estados no intervalo entre 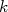 e
e 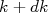 pode ser dado por:
pode ser dado por:
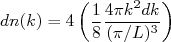 (6)
(6)O fator 4 em (6) surge do fato que podemos dispor de 4 nucleons por nível de energia (2 prótons de spin 1/2 e dois nêutrons de spin 1/2). Devemos também considerar apenas a região da esfera onde as componentes de
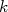 sejam todas positivas, que corresponde a 1/8 do volume total.
sejam todas positivas, que corresponde a 1/8 do volume total.
 .
.A partir de (5) podemos escrever que:
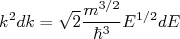 (7)
(7)Substituindo em (6), resulta que:
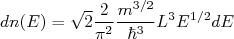 (8)
(8)
O número de estados ocupados nesse modelo é definido pelo número de nucleons presentes no núcleo (A). O último estado de energia ocupado nesse modelo, supondo que todos os estados menos energéticos estejam preenchidos, é denominado energia de Fermi (figura 2) (
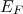 ) e pode ser obtido integrando-se (8), de tal forma que:
) e pode ser obtido integrando-se (8), de tal forma que:
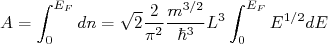 (9)
(9)O que resulta em:
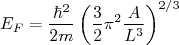 (10)
(10)A expressão (10) representa qual seria a energia de Fermi de um núcleo com A nucleons. Não nos preocupamos se eles são prótons ou nêutrons. Contudo, sabemos que o número de prótons e nêutrons não são iguais em núcleos mais pesados. Isso significa que devemos achar separadamente as energias de Fermi para prótons e nêutrons. Isso pode ser feito da mesma forma. Contudo, devemos modificar o fator 4 em (6) para 2, pois estamos separando os estados de energia para prótons e nêutrons. Dessa forma, podemos calcular as energias de Fermi para prótons e nêutrons como sendo:
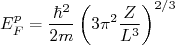 (11)
(11)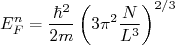 (12)
(12)As expressões (10), (11) e (12) possuem o inconveniente de manter o tamanho da caixa como parâmetro do modelo. Isso é um incômodo, ainda mais pelo fato de assumirmos uma caixa quadrada. Sem perder generalização pode-se chegar a expressões similares a essas, independente do formato da caixa, partindo de densidades volumétricas de partículas, ou seja, densidade de massa,
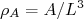 , de prótons,
, de prótons, 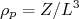 , ou densidade de nêutrons,
, ou densidade de nêutrons, 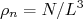 . Assim, (10), (11) e (12) podem ser reescritas como:
. Assim, (10), (11) e (12) podem ser reescritas como:
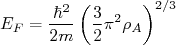 (13)
(13)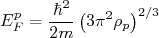 (14)
(14)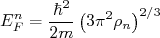 (15)
(15)Podemos fazer uma estimativa simples da energia de Fermi para núcleos. Supondo a densidade típica de um núcleo como sendo:
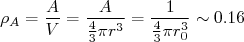 nucleons/fm3 (16)
nucleons/fm3 (16)Resulta em uma energia de Fermi para o núcleo de aproximadamente 37 MeV.
O modelo de Fermi pode ser utilizado para compreender melhor a orígem de alguns aspectos da estabilidade nuclear. A situação mais realista sugere, contudo, que o poço de potencial seja finito. Isso altera levemente o posicionamento dos níveis de energia. Contudo, as características globais do modelo não são alteradas. A partir da energia de Fermi e sabendo que a energia de ligação típica de um núcleon como sendo de aproximadamente 8 MeV, podemos dizer que a profundidade típica do poço de potencial que descreve o núcleo deva ser da ordem de 45 MeV (ver figura 3). Na figura 3-a temos uma representação qualitativa do potencial de interação forte entre os nucleons. Se não houvesse outra interação, o preenchimento de todos os estados até a energia de Fermi resultaria em um número igual de prótons e nêutrons. Trocando um próton por um nêutron, deixaríamos um buraco em um nível de energia abaixo da energia de Fermi e colocaríamos um nucleon em um nível acima da energia de Fermi. Esse nucleon acima do nível de Fermi teria energia de ligação menor que no sistema totalmente preenchido tornando, portanto, o núcleo mais instável. Essa situação sugeriria que o sistema nuclear mais estável seria composto por um número igual de prótons e nêutrons.
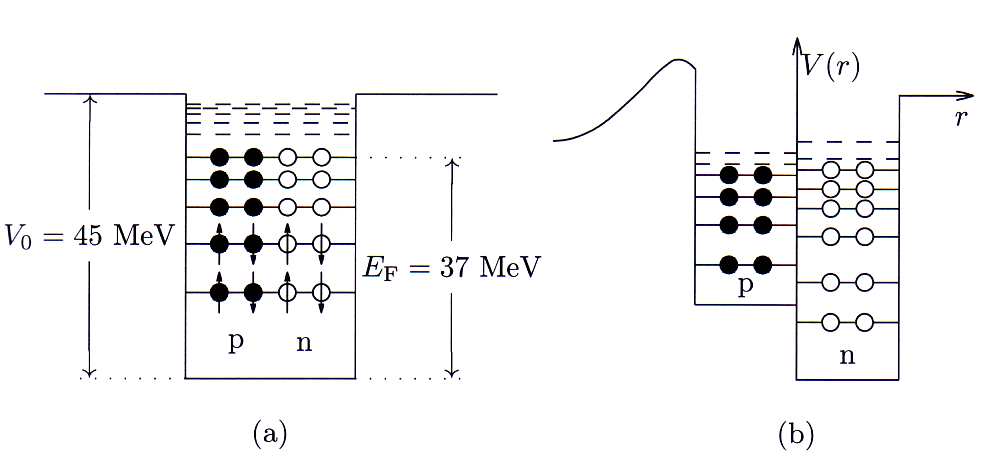
Contudo, não podemos desprezar o fato de existir interação coulombiana entre os prótons no nucleon. Assim, apenas para os prótons, devemos somar a esse poço de potencial, o potencial coulombiano. Isso faz com que o potencial de interação para prótons seja menos profundo que o potencial de interação para nêutrons, como mostrado na figura 3-b. O preenchimento de nucleons até o nível de Fermi, nesse caso, resulta em um número menor de prótons relativo ao número de nêutrons. Como o potencial coulombiano é de longo alcance, dependendo da carga total do núcleo, quanto maior o número atômico, mais raso se torna o poço de potencial para prótons, tornando o número de protons cada vez menor em relação ao número de nêutrons em um núcleo. Isso está em concordância com as observações que núcleos estáveis tendem a ter menos prótons que nêutrons.
Outra característica interessante que podemos construir a partir do modelo de Fermi diz respeito à estabilidade por decaimento beta. Suponha um núcleo fora da linha de estabilidade, por exemplo, com excesso de nêutrons. Nesse caso, teríamos um excesso de nêutrons acima do nível de Fermi e a diferença de energia entre o nível ocupado pelo nêutron e o último nível ocupado pelo próton pode ser tal que o decaimento beta seja permitido energéticamente. A figura 4 mostra um esquema de como os preenchimentos de níveis de Fermi para um sistema de A = 7 impossibilita núcleos com excesso de prótons ou nêutrons e como o decaimento beta resulta em núcleos estáveis com Z aproximadamente igual a N.
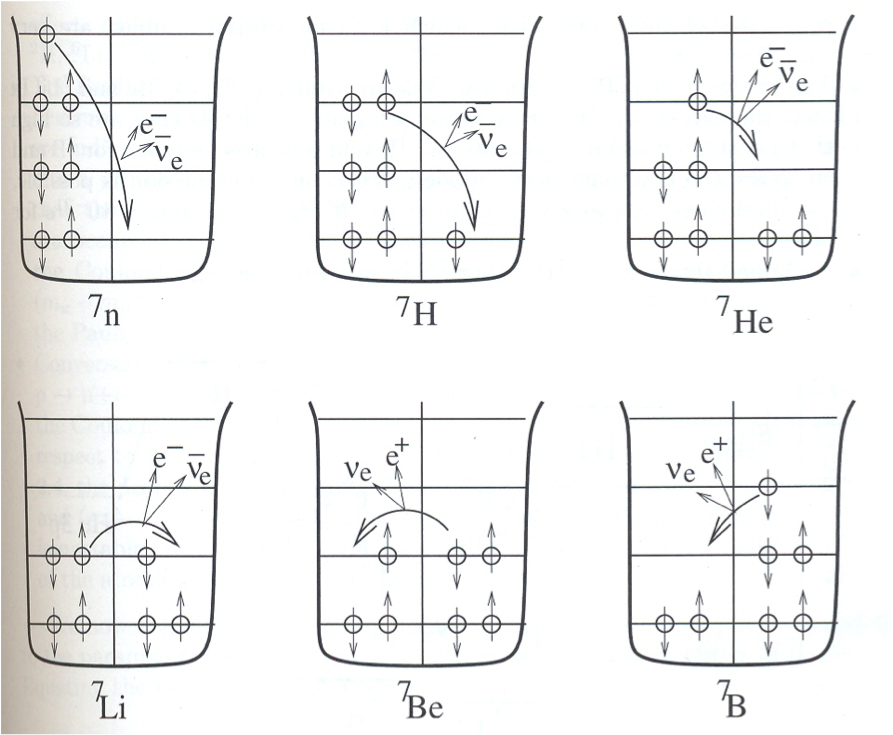
Pode-se explicar também, utilizando o modelo de Fermi, porque praticamente não existem núcleos ímpar-ímpar estáveis. A diferença entre o poço de potencial para prótons e nêutrons e o fato de haver um próton e um nêutron desemparelhados, cada qual em seu nível de energia, criam condições para que a diferença entre esses níveis de energia que contém esses nucleons desemparelhados permita o decaimento beta desse núcleo para um estado par-par.
O fato de o modelo de Fermi ser capaz de explicar qualitativamente a estabilidade do decaimento beta e o equilíbrio entre prótons e nêutrons no núcleo sugere o questionamento se esse modelo poderia explicar o termo de assimetria entre prótons e nêutrons na fórmula semi-empírica de massa, que discutimos no começo do curso. A partir das equações (10), (11) e (12), podemos escrever a energia de Fermi para prótons e nêutrons como sendo:
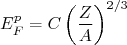 (17)
(17)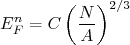 (18)
(18)A energia total presente no gás corresponde à soma das energias de cada nucleon. Podemos calcular a energia acumulada separadamente por prótons e nêutrons (exercício), como sendo:
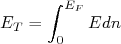 (19)
(19)Que resulta, para prótons e nêutrons:
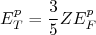 (20)
(20)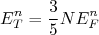 (21)
(21)Assim, a energia total contida no gás de Fermi corresponde à soma de (20) e (21). Substituindo também (17) e (18), resulta em:
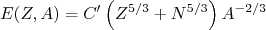 (22)
(22)Devemos impor que
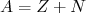 . Assim, o menor valor de energia em (22) ocorre quando o número de prótons é igual ao número de nêutrons. Assim, podemos escrever que a diferença de energia entre (22) e esse mínimo vale:
. Assim, o menor valor de energia em (22) ocorre quando o número de prótons é igual ao número de nêutrons. Assim, podemos escrever que a diferença de energia entre (22) e esse mínimo vale:
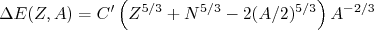 (23)
(23)Definindo
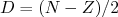 como sendo a assimetria entre o número de prótons e nêutrons no núcleo, podemos reescrever (23) em termos dessa grandeza. Assumindo que esse número seja pequeno, podemos fazer uma expansão em Taylor em
como sendo a assimetria entre o número de prótons e nêutrons no núcleo, podemos reescrever (23) em termos dessa grandeza. Assumindo que esse número seja pequeno, podemos fazer uma expansão em Taylor em 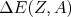 (exercício) resultando em:
(exercício) resultando em:
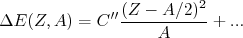 (24)
(24)que corresponde ao termo de assimetria da fórmula de massa.
Apesar da extrema simplicidade desse modelo, capaz de descrever algumas propriedades macroscópicas do núcleo, o modelo de Fermi não é capaz de explicar muitas outras características nucleares, como a distribuição dos níveis de energia do núcleo, momentos angulares dos nucleons, momentos eletromagnéticos, etc. Contudo, essa simplicidade serve de motivação para criar modelos efetivos mais complexos para o núcleo, nos quais essas outras propriedades tornam-se mais evidentes. É o que exploraremos a seguir, através do modelo de camadas nuclear.
Exercícios
- Mostre (20) ou (21).
- Encontre
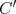 em (22).
em (22).
- Mostre (24). Encontre
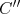 e compare seu valor numérico com o termo de assimetria da fórmula de massa.
e compare seu valor numérico com o termo de assimetria da fórmula de massa.
Leitura recomendada
- Fundamentals of Nuclear Physics, N. A. Jelley, capítulo 2.2.3.
- Introdução à Física Nuclear, H. Schechter e C. A. Bertulani, capítulo 4.3.
- Introduction to Nuclear and Particle Physics, A. Das e T. Ferbel, capítulo III.




No comments