Alguns aspectos da força nuclear
Notas de aula são propriedade intelectual. Sendo assim, qualquer uso, no todo ou em parte, deve ter a origem referenciada apropriadamente, após autorização de seu autor.
O texto a seguir corresponde à anotações parciais de aula. Não é um texto em forma final, completo e totalmente revisado. Nesse caso, esse texto não tem como objetivo substituir livros sobre o assunto. Assim, esse texto deve ser entendido apenas como um guia de estudo para o aluno acompanhar a disciplina.
Nesse ponto colecionamos informações suficientes para tentar descrever a força forte entre dois nucleons. Muitos dos seus aspectos podem ser extraídos das propriedades gerais do núcleo, como distribuições de carga/massa, energia de ligação e momentos eletromagnéticos. Contudo, é através do estudo de sistemas de dois nucleons, como p-p, p-n e n-n, que podemos construir um potencial de interação mais abrangente. O estudo de sistemas de dois nucleons se dá através da investigação dos estados ligados (nesse caso, apenas o dêuteron) ou através de reações de espalhamento. Vamos explorar alguns desses aspectos a seguir.
A força entre dois nucleons e suas propriedades
Vamos considerar que o pontencial de interação entre dois nucleons é devido à contribuição de vários efeitos distintos. Esses efeitos serão incluídos um a um, respeitando algumas invariâncias. Na verdade, para ser mais abrangente, vamos construir esse potencial considerando apenas que, em interações fortes, devemos respeitar conservação de paridade em interações fortes e também a invariância por inversão temporal. Inversão temporal significa que a taxa de uma reação deva ser a mesma se invertemos o tempo, ou seja,
deva ser a mesma se invertemos o tempo, ou seja, 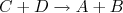 . Em física de partículas há alguns processos nos quais essa inversão temporal não é respeitada, como em alguns decaimentos de káons. Contudo, em física nuclear, ainda não foi observada violação de simetria temporal.
. Em física de partículas há alguns processos nos quais essa inversão temporal não é respeitada, como em alguns decaimentos de káons. Contudo, em física nuclear, ainda não foi observada violação de simetria temporal.
A força nuclear é predominantemente central
Muitas propriedades nucleares, como distribuições de carga/massa, energia de ligação do dêuteron, etc. foram obtidas supondo que o potencial de interação é central, ou seja, depende apenas da distância entre os núcleos. Com essa simplificação conseguimos explicar razoavelmente esses observávies. Dessa forma, é razoável pensar que o fator dominante na interação entre dois núcleos é uma componente central. Assim, tomamos como base um potencial para esse pontencial e adicionaremos termos de correção que, a princípio, devem ser pequenos mas podem ser significativos para explicar de forma precisa algumas características do núcleo.
para esse pontencial e adicionaremos termos de correção que, a princípio, devem ser pequenos mas podem ser significativos para explicar de forma precisa algumas características do núcleo.
Dependência do potencial com o spin dos nucleons
Da aula passada nós concluímos que a seção de choque de espalhamento para baixas energias é composta apenas pelo termo de momento angular orbital nulo, ou seja: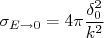 (1)
(1)Vamos calcular a seção de choque de espalhamento entre próton e nêutron nesse limite. Vamos assumir, como ponto de partida, que o potencial é central e igual àquele calculado para o dêuteron, ou seja, um poço quadrado com profundidade
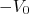 e raio
e raio 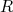 . Nessa situação podemos escrever que a função de onda pode ser decomposta em um termo radial
. Nessa situação podemos escrever que a função de onda pode ser decomposta em um termo radial 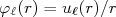 e um termo angular, descrito através de harmônicos esféricos. Nesse caso, a equação para a parte radial é:
e um termo angular, descrito através de harmônicos esféricos. Nesse caso, a equação para a parte radial é:
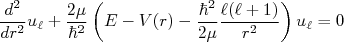 (2)
(2)No caso de
 , a equação (2) torna-se:
, a equação (2) torna-se:
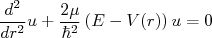 (3)
(3)A equação (3) pode ser resolvida em duas partes (
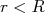 e
e 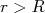 ), resultando:
), resultando:
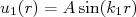 com
com 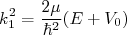 para
para 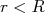 (4)
(4) com
com 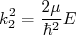 para
para 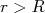 (5)
(5)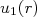 já satisfaz a condição de ser nula na origem. Aplicando-se as condições de contorno de continuidade da função de onda e sua derivada em
já satisfaz a condição de ser nula na origem. Aplicando-se as condições de contorno de continuidade da função de onda e sua derivada em 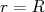 , temos:
, temos:
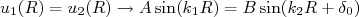 (6)
(6)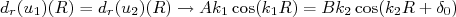 (7)
(7)Dividindo (6) por (7) temos:
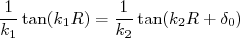 (8)
(8)Tomando o limite
 pois estamos interessados em espalhamento no limite de baixas energias, temos:
pois estamos interessados em espalhamento no limite de baixas energias, temos:
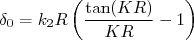 com
com 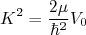 (9)
(9)Substituindo (9) em (1), lembrando que, nesse caso,
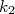 equivale à
equivale à 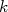 , temos que a seção de choque no limite de baixas energias vale:
, temos que a seção de choque no limite de baixas energias vale:
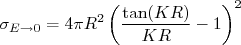 (10)
(10)Vamos utilizar os valores de potencial e raio utilizados durante o nosso estudo do dêuteron. Utilizamos
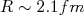 e
e 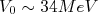 . Note que esses valores foram obtidos supondo que o dêuteron encontrava-se no estado de spin
. Note que esses valores foram obtidos supondo que o dêuteron encontrava-se no estado de spin  ou seja, um estado de tripleto de spin. Substituindo em (10) obtemos que a seção de choque para a situação de tripleto de spin vale
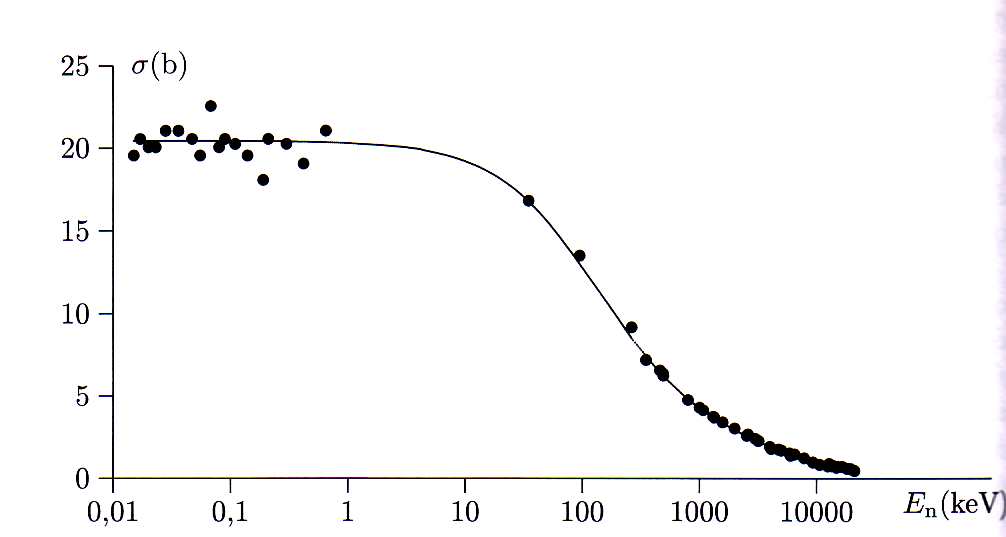
ou seja, um estado de tripleto de spin. Substituindo em (10) obtemos que a seção de choque para a situação de tripleto de spin vale  b. A figura 1 mostra a seção de choque de espalhamento n-p em função da energia. Note que, para energias muito pequenas,
b. A figura 1 mostra a seção de choque de espalhamento n-p em função da energia. Note que, para energias muito pequenas, 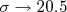 b. Esse valor é incompatível com o obtido para o estado de tripleto de spin.
b. Esse valor é incompatível com o obtido para o estado de tripleto de spin.
A discrepância entre o valor obtido e o experimental indica uma dependência da profundidade do potencial do o estado de spin do sistema. Como essas medidas foram realizadas com feixes não polarizados, todos os estados de spin são igualmente prováveis. Nesse caso, temos dois estados possíveis,
 e
e  . Como o estado
. Como o estado  é tripleto ele contribui com 3/4 da seção de choque total. Assim, a seção de choque total vale:
é tripleto ele contribui com 3/4 da seção de choque total. Assim, a seção de choque total vale:
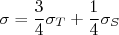 (11)
(11)Substituindo o valor experimental e o valor calculado para o estado de tripleto temos que a seção de choque para o estado de singleto deve ser aproximandamente
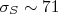 b, muito maior que para o outro estado! Utilizando esse valor em (10) temos como consequência que a profundidade do potencial de interação, quando nesse estado de spin, é muito menor que no estado de tripleto, indicando claramente uma dependência da interação forte entre os nucleons com o spin das partículas interagentes.
b, muito maior que para o outro estado! Utilizando esse valor em (10) temos como consequência que a profundidade do potencial de interação, quando nesse estado de spin, é muito menor que no estado de tripleto, indicando claramente uma dependência da interação forte entre os nucleons com o spin das partículas interagentes.
Com base nessa evidência, podemos tentar adicionar um termo de correção ao potencial central
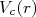 que dependa do spin. Há várias formas de se fazer isso. Podemos dizer que há uma correção que dependa de
que dependa do spin. Há várias formas de se fazer isso. Podemos dizer que há uma correção que dependa de  ,
, 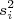 ,
, 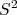 ,
,  , etc. Muitos desses termos não satisfazem as invariâncias que admitimos inicialmente. O termo mais simples que podemos utilizar é aquele que depende de
, etc. Muitos desses termos não satisfazem as invariâncias que admitimos inicialmente. O termo mais simples que podemos utilizar é aquele que depende de  . Assim, vamos adicionar ao termo central um termo de spin na forma:
. Assim, vamos adicionar ao termo central um termo de spin na forma:
 (12)
(12)O produto escalar em (12) pode ser escrito em termos do spin total, como fizemos nos cálculos de momentos eletromagnéticos. Assim:
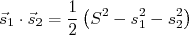 (13)
(13)que resulta em:
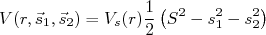 (14)
(14)O efeito desse potencial pode ser estimado calculando-se o valor médio de (13) para os estados de tripleto (
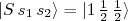 ) e singleto (
) e singleto ( 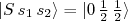 ), lembrando que
), lembrando que 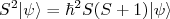 . Assim, para o estado de tripleto e singleto temos:
. Assim, para o estado de tripleto e singleto temos:
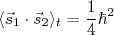 (15)
(15)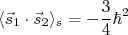 (16)
(16)Se
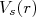 em (14) for atrativo, ou seja, negativo, o efeito do acoplamento de spin para o estado singleto é deixar o potencial menos atrativo (mais raso) que para o estado de tripleto, aumentando a seção de choque para esse estado, como observado nos dados. O valor e forma de
em (14) for atrativo, ou seja, negativo, o efeito do acoplamento de spin para o estado singleto é deixar o potencial menos atrativo (mais raso) que para o estado de tripleto, aumentando a seção de choque para esse estado, como observado nos dados. O valor e forma de 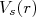 pode ser obtido através do ajuste dos dados experimentais para seção de choque de espalhamento entre prótons e nêutrons em função da energia.
pode ser obtido através do ajuste dos dados experimentais para seção de choque de espalhamento entre prótons e nêutrons em função da energia.
Caráter não central da força entre dois nucleons - termo tensorial
Quando tentamos explicar o momento de dipolo magnético do dêuteron e contruir a sua função de onda, sentimos a necessidade de misturar estados de momentos angular orbital diferentes. Na verdade, vimos que o dêuteron possui uma fração da ordem de 4% de estados D. Isso é um forte indício de que o momento angular orbital não é uma constante de movimento. A implicação disso é que o potencial de interação não é mais central, ou seja, não depende apenas da distância entre as partículas mas depende também da orientação relativa entre elas. Como a mistura é pequena, essa "não centralidade" do potencial possa ser uma pequena correção a ser incluida no potencial nuclear, como fizemos para o caso de spin, discutido anteriormente.Se o potencial não é mais central deve depender da orientação relativa entre os nucleons interagentes. Escolhe-se, nesse caso, como orientação preferencial, o spin desses nucleons. Assim, toma-se a projeção do vetor posição na direção do spin (
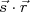 )como forma de estabelecer a dependência angular com o potencial. Como devemos respeitar a consevação de paridade, esse termo do potencial deve ser uma função par, ou seja, o vetor posição deve aparecer pelo menos quadraticamente. Além disso, devemos considerar a orientação dos dois nucleons para construção desse potencial. Assim, é comum escrevê-lo na forma
)como forma de estabelecer a dependência angular com o potencial. Como devemos respeitar a consevação de paridade, esse termo do potencial deve ser uma função par, ou seja, o vetor posição deve aparecer pelo menos quadraticamente. Além disso, devemos considerar a orientação dos dois nucleons para construção desse potencial. Assim, é comum escrevê-lo na forma 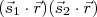 . Ademais, deseja-se que, na média sobre todas as direções, o efeito desse termo seja nulo. Para isso, subtrai-se o valor médio do produto escalar escrito anteriormente. Dessa forma, é comum escrever esse termo de potencial como sendo:
. Ademais, deseja-se que, na média sobre todas as direções, o efeito desse termo seja nulo. Para isso, subtrai-se o valor médio do produto escalar escrito anteriormente. Dessa forma, é comum escrever esse termo de potencial como sendo:
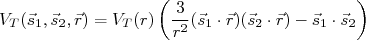 (17)
(17)O produto escalar entre os spins em (17) é necessário para satisfazer o critério de média nula desse termo. A inclusão desse termo não estabelece um novo comportamento para a força nuclear uma vez que o acoplamento entre spins já é um termo presente no potencial, como descrevemos anteriormente. O termo
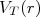 , assim como no caso anterior, é ajustado de modo a reproduzir as observações experimentais. Esse termo é chamado de componente tensorial da força nuclear.
, assim como no caso anterior, é ajustado de modo a reproduzir as observações experimentais. Esse termo é chamado de componente tensorial da força nuclear.
Não localidade da força nuclear - acoplamento spin-órbita
Potenciais que dependem apenas da posição são chamados de potenciais locais. Conhecendo-se a posição no espaço, determina-se o valor do potencial. Contudo, há muitos casos na física onde surgem potenciais não locais, ou seja, aqueles que, além da posição, dependem da velocidade relativa entre as partículas. Um potencial não local é o acoplamento spin-órbita, que surge em física atômica para explicar a estrutura fina dos níveis de energia atômicos e surge também na física nuclear.Uma grande evidência da existência de interação spin-órbita na força nuclear diz respeito a medidas de polarização em espalhamento. Polarização é definida como sendo a diferença entre o número de partículas com spin apontando em um sentido e em outro pelo número total de partículas observadas, ou seja:
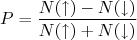 (18)
(18)Um conjunto de partículas totalmente polarizada para cima possui
 , enquanto um feixe de partículas totalmente polarizado para baixo possui
, enquanto um feixe de partículas totalmente polarizado para baixo possui 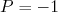 . Um feixe não polarizado possui
. Um feixe não polarizado possui  . O acoplamento spin-órbita, em geral, é escrito em primeira ordem como sendo:
. O acoplamento spin-órbita, em geral, é escrito em primeira ordem como sendo:
 (19)
(19)Assim como nos outros termos, a amplitude radial é obtida a partir do ajuste sistemático aos dados experimentais. Observando a equação (19), concluímos que, caso o momento angular esteja no mesmo sentido que o spin total, temos que o acoplamento é positivo, sendo o potencial resultante de mesmo sinal que a amplitude radial. Caso o sentido do momento angular orbital seja oposto ao spin, o acoplamento é negativo. Assim, dependendo desse acoplamento, podemos ter uma interação atrativa ou repulsiva devido a esse termo.
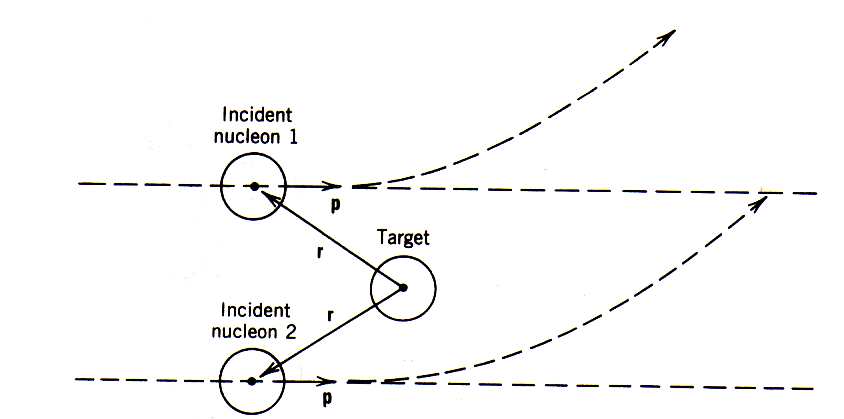
Como esse acoplamento reflete na polarização de uma medida experimental. Imagine a situação esquematizada na figura 2. Nessa figura, feixe e alvo possuem spin no mesmo sentido (nessa figura, apontando para fora da tela). A partícula 1 (no topo), em relação ao alvo, possui momento angular cujo sentido penetra na tela (
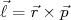 ), tornando o acoplamento negativo. Se
), tornando o acoplamento negativo. Se 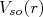 for atrativo, o potencial spin-órbita resulta em um potencial repulsivo, afastando a partícula do alvo. No caso da partícula 2, (na parte inferior da figura), o momento angular orbital e spin total possuem o mesmo sentido, tornando o acoplamento positivo. Nesse caso, a interação resultante é atrativa, aproximando a partícula do feixe em direção ao alvo.
for atrativo, o potencial spin-órbita resulta em um potencial repulsivo, afastando a partícula do alvo. No caso da partícula 2, (na parte inferior da figura), o momento angular orbital e spin total possuem o mesmo sentido, tornando o acoplamento positivo. Nesse caso, a interação resultante é atrativa, aproximando a partícula do feixe em direção ao alvo.
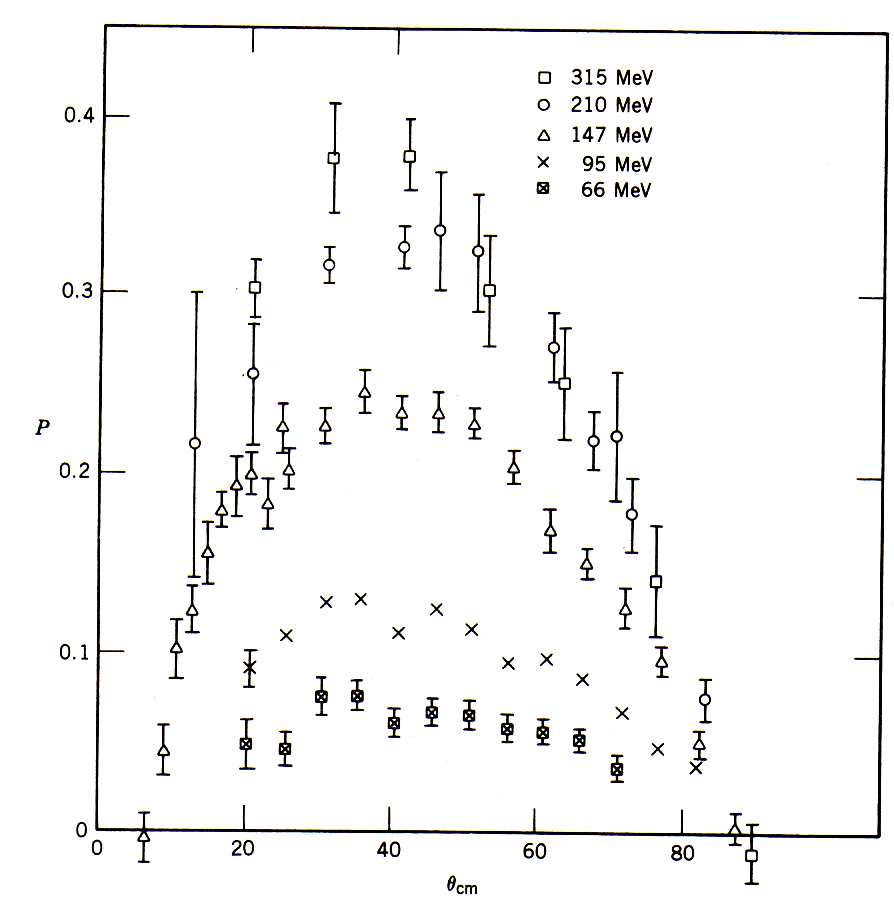
Como, estatisticamente, o feixe pode incidir igualmente acima ou abaixo do alvo, caso as partículas interagentes possuam spin de mesmo sentido, há a preferência para que elas sejam desviadas em uma direção preferencial. Partículas com spins em sentidos opostos não teriam preferência de desvio pois o spin total seria nulo e não existiria o acoplamento spin-órbita. Essa direção preferencial de desvio resultaria na polarização parcial do feixe espalhado em uma direção. Na figura 3 temos dados de polarização em função do ângulo de espalhamento para reações de diferentes energias. Como vimos, na medida em que diminuímos a energia, favorecemos espalhamentos de onda S, ou seja, sem momento angular orbital. Nesse caso, a polarização seria menor. Quando aumentamos a energia, momentos angulares orbital de maior valor contribuem mais intensamente para a seção de choque, aumentando a polarização.
Força nuclear em curtas distâncias
Quando estudamos a massa nuclear, através do modelo da gota líquida, e a distribuição de massa/carga, temos implícita uma característica importante da força nuclear, que surge das evidências de que a densidade de matéria nuclear é aproximadamente constante no interior do núcleo. Essa constância indica que há um limite de distância para a separação entre dois nucleons. Se a força for puramente atrativa, a densidade nuclear deveria variar drasticamente quando colocamos mais nucleons dentro do núcleo. Assim, temos uma evidência de que, a curtas distâncias, a força nuclear deixa de ser atrativa e se torne repulsiva. O equilíbrio entre essas duas componentes resulta na densidade aproximadamente constante.Uma forma de verificar essa característica é realizar medidas de seção de choque total neutron-próton em função da energia. Pode-se medir, a partir dessas seções de choque, o deslocamento de fase (
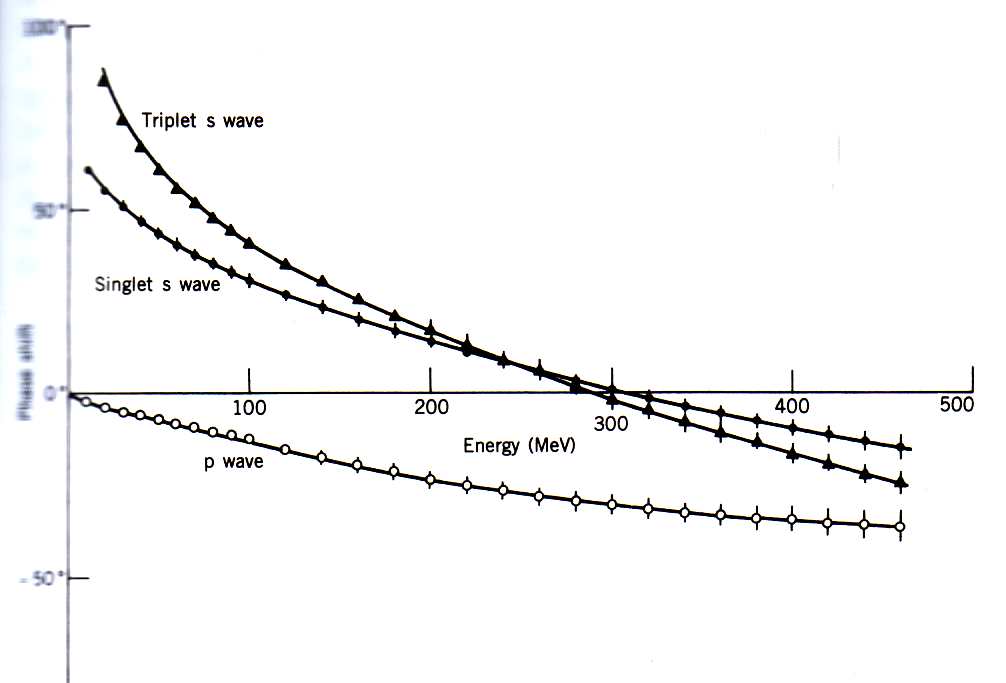
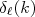 ) para cada componente de onda parcial. Já vimos que deslocamentos de fase positivos indicam um potencial atrativo enquanto deslocamentos negativos indicam um potencial repulsivo. Quando maior a energia do feixe, menores as distâncias investigadas para um dado momento angular. Na figura 4 mostramos o deslocamento de fase em função da energia para alguns momentos angulares. O importante é observar os deslocamentos de fase para ondas S. Nesse caso, vários termos do potencial nuclear, discutidos anteriormente, não contribuem para a interação e a interpretação dos dados torna-se mais direta. Note que para energias de aproximadamente 300 MeV o sinal da fase se inverte. Para baixas energias o potencial é atrativo enquanto que, para altas energias, o potencial torna-se repulsivo.
) para cada componente de onda parcial. Já vimos que deslocamentos de fase positivos indicam um potencial atrativo enquanto deslocamentos negativos indicam um potencial repulsivo. Quando maior a energia do feixe, menores as distâncias investigadas para um dado momento angular. Na figura 4 mostramos o deslocamento de fase em função da energia para alguns momentos angulares. O importante é observar os deslocamentos de fase para ondas S. Nesse caso, vários termos do potencial nuclear, discutidos anteriormente, não contribuem para a interação e a interpretação dos dados torna-se mais direta. Note que para energias de aproximadamente 300 MeV o sinal da fase se inverte. Para baixas energias o potencial é atrativo enquanto que, para altas energias, o potencial torna-se repulsivo.
A forma mais comum de modelar esse potencial repulsivo a curtas distâncias, pensando na imcompressibilidade da matéria nuclear em condições normais, é assumir que o potencial seja infinito abaixo de uma certa distância, tornando a penetração impossível. Assim, esse termo repulsivo para a força nuclear pode ser escrito como:
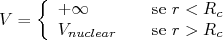 (20)
(20)onde
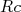 é ajustado de modo a reproduzir os dados mostrados na figura 4, por exemplo. Valores razoávais para esse raio são
é ajustado de modo a reproduzir os dados mostrados na figura 4, por exemplo. Valores razoávais para esse raio são  fm.
fm.
Conclusão
Exploramos alguns aspectos da força nuclear para construir um potencial de interação entre dois nucleons. O potencial construído é extremamente repulsivo à curtas distâncias (menores que aproximadamente 0.5 fm) e possui uma série de contribuições para distâncias maiores que 0.5 fm. Em resumo, podemos escrever o potencial de interação entre dois nucleons como sendo: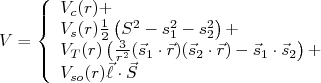 (21)
(21)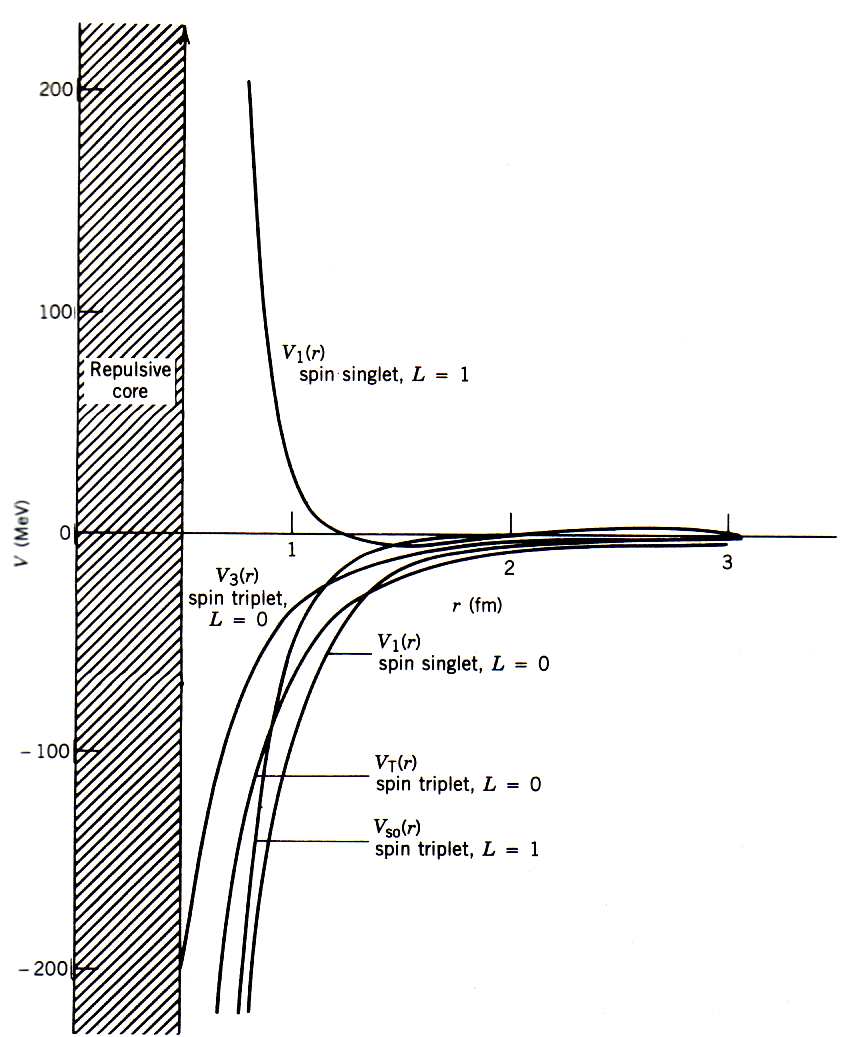
Na figura 5 mostramos o potencial de interação nucleon-nucleon em diferentes situações. Esse potencial empírico possui um sucesso razoável em explicar vários observáveis experimentais mas a descrição da interação entre nucleons não é completa. Poderíamos adicionar outros termos de ordem maior, por exemplo correções de
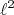 ou
ou 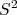 ou até fazer com que os termos radiais dependessem do momento angular. Isso mostra a complexidade da tarefa que é descrever a interação forte. O problema torna-se mais complexo quando pensamos na interação entre muitos nucleons, por exemplo em um núcleo de oxigênio-16, composto de 8 prótons e 8 nêutrons. O cálculo do potencial resultante, a partir da soma dois a dois entre nucleons é muito difícil, senão impossível. Para contornar essa dificuldade mas permitindo que se entenda aspectos fundamentais da estrutura nuclear, criou-se modelos efetivos de interação, no qual assumimos que essa soma dois a dois resulte em valores médios nulos para muitos dos termos do potencial de interação nucleon-nucleon para que possamos descrever núcleos complexos a partir de potenciais efetivos bastante simplificados. O custo seria a menor precisão na reprodução de observáveis, porém compensado pela melhor compreensão dos mecanismos mais importantes de interação nuclear. Alguns desses modelos serão explorados a seguir. Iniciaremos com o modelo de gás de Fermi e seguiremos com a descrição do modelo de camadas nuclear.
ou até fazer com que os termos radiais dependessem do momento angular. Isso mostra a complexidade da tarefa que é descrever a interação forte. O problema torna-se mais complexo quando pensamos na interação entre muitos nucleons, por exemplo em um núcleo de oxigênio-16, composto de 8 prótons e 8 nêutrons. O cálculo do potencial resultante, a partir da soma dois a dois entre nucleons é muito difícil, senão impossível. Para contornar essa dificuldade mas permitindo que se entenda aspectos fundamentais da estrutura nuclear, criou-se modelos efetivos de interação, no qual assumimos que essa soma dois a dois resulte em valores médios nulos para muitos dos termos do potencial de interação nucleon-nucleon para que possamos descrever núcleos complexos a partir de potenciais efetivos bastante simplificados. O custo seria a menor precisão na reprodução de observáveis, porém compensado pela melhor compreensão dos mecanismos mais importantes de interação nuclear. Alguns desses modelos serão explorados a seguir. Iniciaremos com o modelo de gás de Fermi e seguiremos com a descrição do modelo de camadas nuclear.
Exercícios
- Admita que o potencial nuclear tenha somente as componentes repulsiva, radial e termo de spin, ou seja,
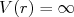 para
para 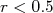 fm e
fm e 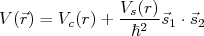 para
para 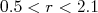 fm. Suponha que
fm. Suponha que 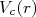 e
e 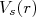 possam ser tratados como poços radiais quadrados, cada um com uma determinada profundidade. Com base nos dados experimentais de energia de ligação do dêuteron e seções de choque de espalhamento n-p em baixas energias, determine a profundidade desses poços.
possam ser tratados como poços radiais quadrados, cada um com uma determinada profundidade. Com base nos dados experimentais de energia de ligação do dêuteron e seções de choque de espalhamento n-p em baixas energias, determine a profundidade desses poços.
- Mostre que a média sobre todas orientações em (17) é nula.
- Suponha uma partícula de spin 1 movendo-se em um potencial central da forma
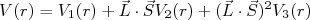 . Obtenha os valores médios desse potencial para estados com J = L+1, L e L-1. Compare os resultados.
. Obtenha os valores médios desse potencial para estados com J = L+1, L e L-1. Compare os resultados.
Leitura recomendada
- Introductory Nuclear Physics, K. S. Krane, capítulo 4.
- Introdução à Física Nuclear, H. Schechter e C. A. Bertulani, capítulos 2 e 9.





Acho que tem um erro de digitação no último exercício, onde está escrito V_3(3) deveria ser V_3® não?