Um pouco mais de teoria de espalhamento: expansão em ondas parciais
Notas de aula são propriedade intelectual. Sendo assim, qualquer uso, no todo ou em parte, deve ter a origem referenciada apropriadamente, após autorização de seu autor.
O texto a seguir corresponde à anotações parciais de aula. Não é um texto em forma final, completo e totalmente revisado. Nesse caso, esse texto não tem como objetivo substituir livros sobre o assunto. Assim, esse texto deve ser entendido apenas como um guia de estudo para o aluno acompanhar a disciplina.
Em teoria de espalhamento vimos que podemos escrever que a função de onda de partículas sob a ação de um potencial é composta por um termo que corresponde à onda incidente e um termo que componente à onda espalhada, ou seja:
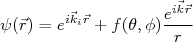 (1)
(1)A função
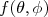 é denominada de amplitude de espalhamento e depende diretamente do potencial de interação. A seção de choque é a razão entre o número de partículas espalhadas e o fluxo incidente, ou seja:
é denominada de amplitude de espalhamento e depende diretamente do potencial de interação. A seção de choque é a razão entre o número de partículas espalhadas e o fluxo incidente, ou seja:
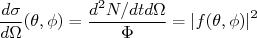 (2)
(2)Vamos inicialmente considerar a natureza do potencial de espalhamento. Muitos potenciais de interação possuem simetria esférica (dependem somente da distância entre o centro espalhador e a partícula). Nesse caso, do ponto de vista teórico, seria interessante explorar essa característica. Isso poderia ser feito se pudéssemos resolver o problema sobre o ponto de vista de espalhamento de ondas esféricas. Para isso precisamos reescrever (1) em termos de ondas esféricas. Partiremos de uma expansão em harmônicos esféricos de uma função qualquer:
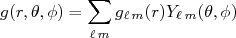 (3)
(3)Para cada termo da soma acima, a constante
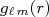 , dependente do raio, pode ser obtida similarmente a termos de uma expansão de Fourier. No caso de uma onda plana, pode-se demonstrar que (veja Landau e Lifshitz):
, dependente do raio, pode ser obtida similarmente a termos de uma expansão de Fourier. No caso de uma onda plana, pode-se demonstrar que (veja Landau e Lifshitz):
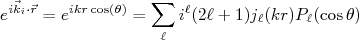 (4)
(4)onde
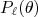 correspondem a polinômios de Legendre, decorrentes da simetria esférica do problema e do fato da onda incidente não depender de
correspondem a polinômios de Legendre, decorrentes da simetria esférica do problema e do fato da onda incidente não depender de  .
. 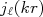 são funções de Bessel esféricas de ordem
são funções de Bessel esféricas de ordem 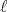 .
.
Como estamos interessados em obter seções de choque precisamos examinar o comportamento assintórico de (4). Como o único termo dependente do raio corresponde às funções de Bessel esféricas, vamos tomar o seu comportamento a distâncias muito grandes do centro espalhador. Nesse caso, pode-se mostrar que:
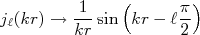 (5)
(5)ou ainda, reescrevendo (5) em termos de exponenciais complexas:
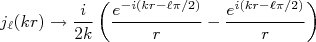 (6)
(6)Substituindo (6) em (4), podemos escrever que uma onda plana corresponde à soma de uma série de ondas esféricas com termos que se aproximam da origem e termos emergentes da origem, ou seja:
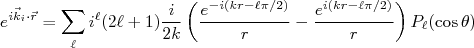 (7)
(7)A descrição acima supõe que não haja potencial de interação. Contudo, devemos incluir o efeito resultante do potencial de interação. No caso da aproximação de Born, visto anteriormente, o problema de condições de contorno foi resolvido através de funções de Green e uma expansão na qual tomamos o termo de primeira ordem. Nesse caso, vamos supor que o potencial de interação é responsável por causar uma modificação na onda emergente da interação. A onda incidente não deve sofrer modificação. Essa modificação, definida como
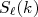 , depende da energia do feixe e do momento angular associado.
, depende da energia do feixe e do momento angular associado. 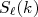 é denominada matriz de espalhamento e deve ser unitária, ou seja
é denominada matriz de espalhamento e deve ser unitária, ou seja  , para conservar probabilidade, nesse caso o número de partículas incidentes ser igual ao número de partículas emergentes. Podemos então escrever a função de onda após interação com o potencial a partir de (7) como:
, para conservar probabilidade, nesse caso o número de partículas incidentes ser igual ao número de partículas emergentes. Podemos então escrever a função de onda após interação com o potencial a partir de (7) como:
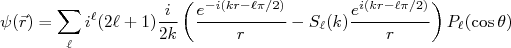 (8)
(8)Vamos tentar manipular (8) de modo a obter algo comparável a (1). Primeira-mente adicionamos e subtraimos uma onda plana emergente de (8). Assim:
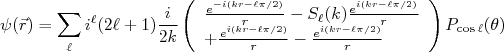 (9)
(9)É fácil ver que:
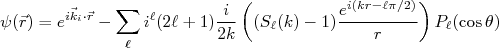 (10)
(10)Em (10), o termo
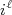 cancela com o termo
cancela com o termo 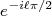 da onda emergente. Assim, rearrumando os termos, temos:
da onda emergente. Assim, rearrumando os termos, temos:
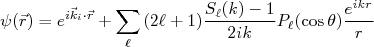 (11)
(11)Comparando (11) com (1) chegamos, finalmente, que a amplitude de espalhamento vale:
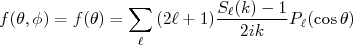 (12)
(12)O conhecimento da matriz de espalhamento permite obter informações dobre o potencial de interação. Nesse caso, essa determinação é feita aplicando-se as condições de contorno no problema, que depende do potencial a ser considerado. Uma forma um pouco mais simples de interpretar a interação com o potencial é escrever a matriz de espalhamento em termos de phase shifts, ou mudanças de fase, que pode depender de cada onda parcial em (12).
No caso de espalhamento elástico, é fácil ver em (5), que o efeito do potencial sobre a função de onda deve ser apenas de introduzir uma fase no termo senoidal. Assim, o efeito do potencial é de transformar:
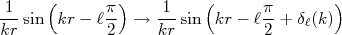 (13)
(13)Escrevendo (13) em termos de exponenciais complexas e comparando com (10) é fácil ver que a matriz de espalhamento pode ser escrita em termos da diferença de fase causada pelo potencial, ou seja:
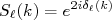 (14)
(14)O fator 2 na exponencial em (14) aparece simplesmente pelo fato de, durante a manipulação algébrica, desejarmos manter a noção de que toda a informação de espalhamento está contida na onda emergente. O uso de defasagens torna a interpretação física do espalhamento mais simples. O número de onda
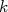 é proporcional à energia cinética da partícula, ou seja
é proporcional à energia cinética da partícula, ou seja 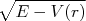 . Se o potencial for atrativo,
. Se o potencial for atrativo, 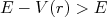 e, na região de potencial, a função de onda oscila com maior frequência espacial. Desse modo, em relação a uma partícula livre, na situação assintótica, a função de onda terá uma fase positiva, ou seja,
e, na região de potencial, a função de onda oscila com maior frequência espacial. Desse modo, em relação a uma partícula livre, na situação assintótica, a função de onda terá uma fase positiva, ou seja, 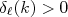 . O contrário ocorre para um potencial repulsivo, fazendo
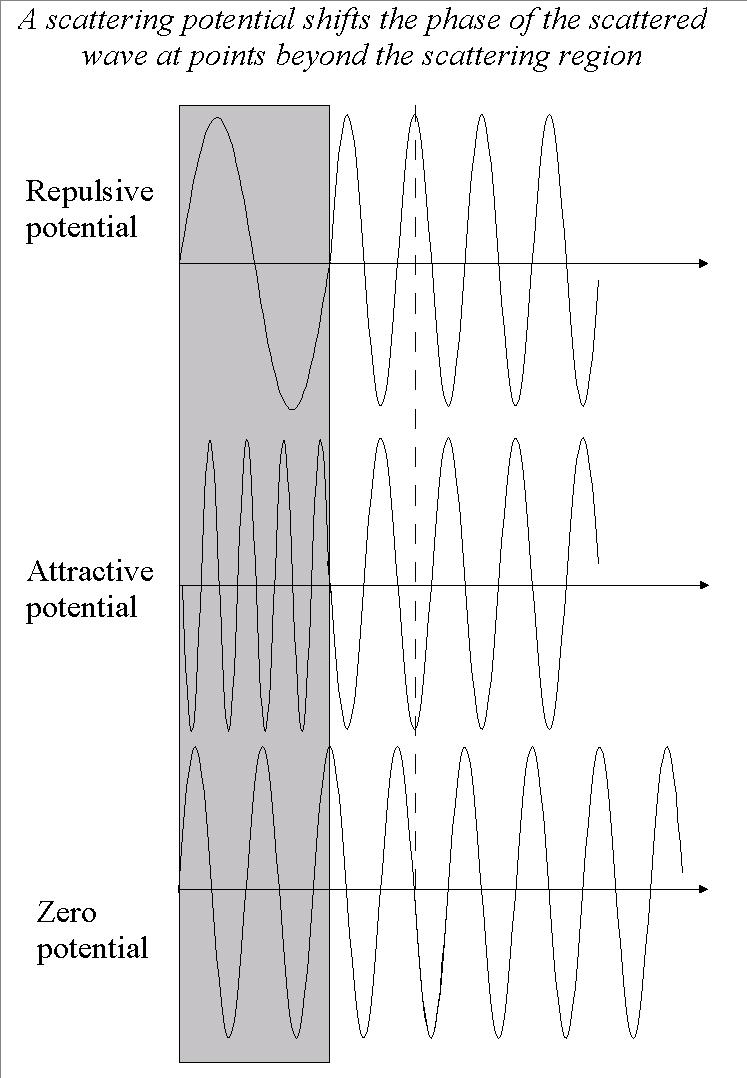
. O contrário ocorre para um potencial repulsivo, fazendo 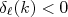 . Um exemplo gráfico pode ser visto na figura 1. Medidas de defasagem, desse modo, permitem determinar a natureza atrativa/repulsiva do potencial de interação.
. Um exemplo gráfico pode ser visto na figura 1. Medidas de defasagem, desse modo, permitem determinar a natureza atrativa/repulsiva do potencial de interação.
Substituindo (14) em (12) pode-se mostrar que:
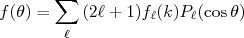 (15)
(15)com
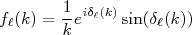 (16)
(16)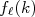 é chamada de amplitude de espalhamento parcial para a onda
é chamada de amplitude de espalhamento parcial para a onda 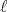 . A partir de (2) podemos calcular a sessão de choque total de espalhamento. Nesse caso, devemos fazer:
. A partir de (2) podemos calcular a sessão de choque total de espalhamento. Nesse caso, devemos fazer:
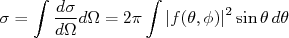 (17)
(17)O termo
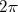 surge da integral em
surge da integral em 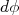 . Substituindo (15) em (17), sabendo que o somente os polinômios de Legendre dependem do ângulo, e desprezando os termos cruzados por conta da ortogonalidade dos polinômios de Legendre, podemos escrever:
. Substituindo (15) em (17), sabendo que o somente os polinômios de Legendre dependem do ângulo, e desprezando os termos cruzados por conta da ortogonalidade dos polinômios de Legendre, podemos escrever:
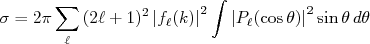 (18)
(18)Sabendo que:
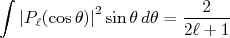 (19)
(19)temos que:
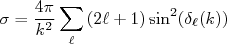 (20)
(20)A expressão acima mostra que a seção de choque total de espalhamento depende das defasagens impostas às ondas parciais devido ao potencial de interação. No limite de baixas energias,
 , podemos simplificar (20). Nesse limite, devido à componente centrífuga do potencial, imposto pelo momento angular, somente
, podemos simplificar (20). Nesse limite, devido à componente centrífuga do potencial, imposto pelo momento angular, somente  pode contribuir para a seção de choque de espalhamento. Assim, para
pode contribuir para a seção de choque de espalhamento. Assim, para  , a seção de choque total de espalhamento fica:
, a seção de choque total de espalhamento fica:
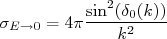 (21)
(21)A seção de choque em (21) somente é finita em baixas energias se o termo senoidal tender a zero. Nesse caso, podemos simplificar (21) de modo à:
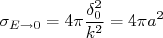 (22)
(22)o termo
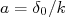 é chamado de comprimento de espalhamento. Da mesma forma que para as defasagens temos
é chamado de comprimento de espalhamento. Da mesma forma que para as defasagens temos 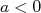 para um potencial repulsivo e
para um potencial repulsivo e 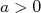 para um potencial atrativo.
para um potencial atrativo.
Exercícios
- Mostre que escrever a matriz de espalhamento como em (14) implica que só há espalhamento elástico, ou seja, os fluxos de partículas incidentes e emergentes com mesmo vetor de onda são iguais.
- Mostre (15) a partir de (12).
- Ache a seção de choque de espalhamento em baixas energias para um potencial
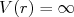 para
para 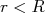 e
e 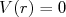 para
para 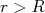 . Dica: calcule o deslocamento de fase aplicando as condições de contorno para a função de onda nesse potencial para
. Dica: calcule o deslocamento de fase aplicando as condições de contorno para a função de onda nesse potencial para  .
.
Leitura recomendada
- Introdução à Física Nuclear, H. Schechter e C. A. Bertulani, capítulos 9.2 e 9.3.




No comments