Testes de hipóteses - o teste-z
Friday 24 August 2012 at 1:10 pm
Versão para impressão
É comum na atividade científica nos depararmos com questionamentos que envolvem a comparação de um resultado obtido através de um experimento (ou de um trabalho teórico), sujeito a incertezas e flutuações, com uma expectativa qualquer, ou com outros resultados de um outro trabalho. Por exemplo: os resultados do LHC suportam a existência do bóson de Higgs? O valor da aceleração que eu obtive é compatível com a aceleração da gravidade em São Paulo, medida pelo IAG? Estas duas molas são iguais, ou seja, têm constantes elásticas e comprimentos compatíveis uma com a outra?
Para isso, existe um tópico de estatística chamado inferência, no qual um dos problemas que é abordado neste tópico é o teste de hipótese. Há vários testes diferentes que dependem do tipo de amostra a ser comparada, suas propriedades e características. Neste texto vamos discutir um pouco o teste-z. Este tem uma aplicação bastante limitada, pois depende de condições que nem sempre (ou raramente) são obtidas em uma amostra. Contudo, por ser um teste bastante simples, sendo fácil compreender os fundamentos que estão por trás dele, é bastante utilizado em disciplinas básicas de laboratório e estatística. Antes disso vamos rever alguns conceitos de probabilidade e densidades de probabilidade.
Probabilidade e densidade de probabilidade
Pode-se definir a probabilidade [1,2] de se obter um determinado resultado como sendo a relação entre o número de vezes que este resultado é obtido em uma amostra e o tamanho desta amostra, quando esta é suficientemente grande, ou seja:
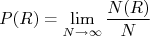
onde 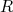 é o resultado que queremos calcular a probabilidade de ocorrência. Em geral esse resultado é definido em termos de um intervalo: qual a probabilidade de encontrar um aluno ingressante na USP entre 35 e 40 anos? Por conta disso, vamos definir a probabilidade de encontrar, em uma amostra suficientemente grande, um resultado no intervalo de
é o resultado que queremos calcular a probabilidade de ocorrência. Em geral esse resultado é definido em termos de um intervalo: qual a probabilidade de encontrar um aluno ingressante na USP entre 35 e 40 anos? Por conta disso, vamos definir a probabilidade de encontrar, em uma amostra suficientemente grande, um resultado no intervalo de  e
e 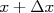 como sendo [1]:
como sendo [1]:
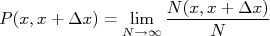
É obvio que, quanto mais amplo o intervalo, maior a probabilidade de encontrar um resultado neste intervalo. Para eliminar essa dependência, define-se a função densidade de probabilidade (F.D.P.) de tal forma que a probabilidade de encontrar um resultado em um intervalo entre  e
e 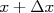 e [1]:
e [1]:
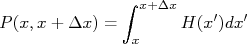
Sendo 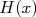 a densidade de probabilidade de ocorrer um evento
a densidade de probabilidade de ocorrer um evento  . Podemos escrever então que a função densidade de probabilidade é:
. Podemos escrever então que a função densidade de probabilidade é:
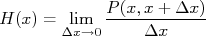
Por ter um significado de densidade, a função densidade de probabilidade é sempre positiva. Ademais, podemos escrever que, como a probabilidade de ocorrer qualquer evento é 1, a relação:
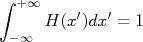
Deve ser sempre satisfeita. Em estatística encontramos diversas funções de densidade de probabilidade, tais como a binomial, poison, gaussiana, etc. [1,2], sendo esta última bastante comum, principalmente em experimentos didáticos.
Conhecendo-se a função densidade de probabilidade de uma determinada grandeza é fácil calcular probabilidades de determinado evento ocorrer. Por exemplo, podemos pensar em responder qual é a probabilidade de se obter, em uma medida, um valor inferior à 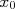 . Conhecendo-se a F.D.P. basta resolver:
. Conhecendo-se a F.D.P. basta resolver:
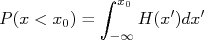
Ou, por exemplo, qual é a probabilidade de um determinado valor ser superior à 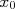 ? Da mesma forma, escrevemos:
? Da mesma forma, escrevemos:
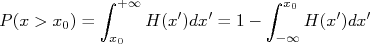
Da mesma forma, podemos nos perguntar qual é a probabilidade de encontrar 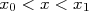 . Em termos de densidade de probabilidade a resposta é:
. Em termos de densidade de probabilidade a resposta é:
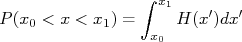
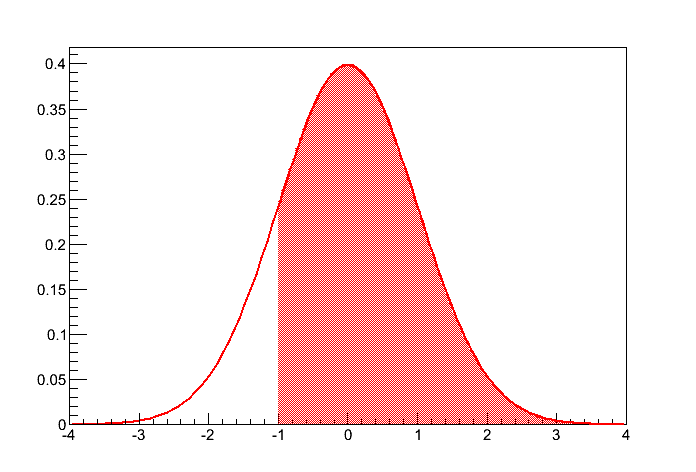
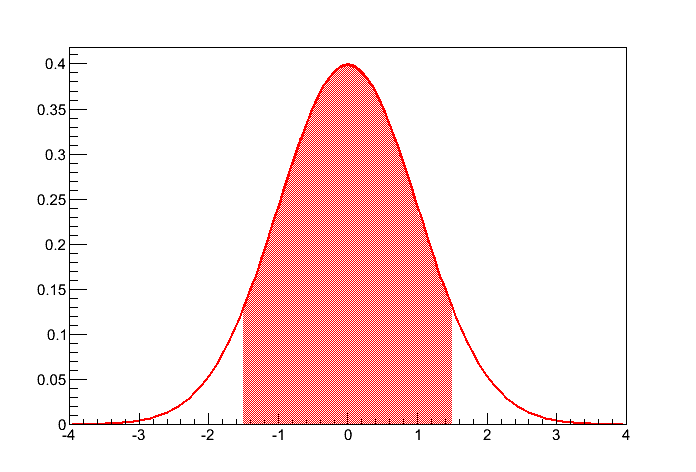
Vamos tomar como exemplo uma função densidade de probabilidade gaussiana de média zero e desvio padrão 1. Nas figuras 1 a 3 são mostrados alguns exemplos da relação entre a integral da F.D.P. e a probabilidade de obter um evento em determinada região.
Figura 1 - A área pintada corresponde à probabilidade de se obter um evento com 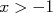 .
.
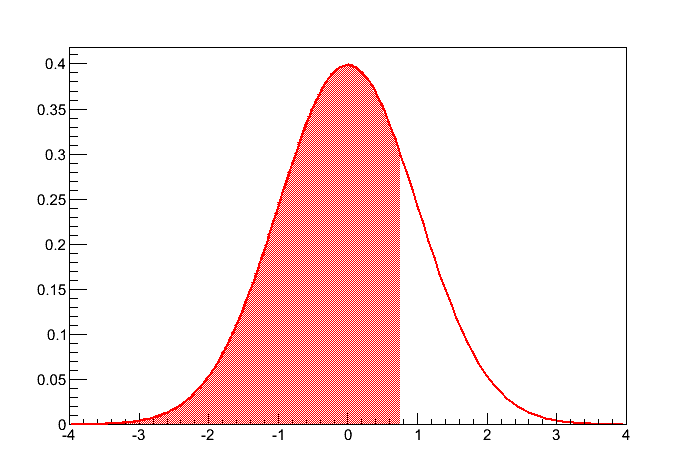
Figura 2 - A área pintada corresponde à probabilidade de se obter um evento com 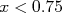 .
.
Figura 3 - A área pintada corresponde à probabilidade de se obter um evento com 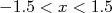 .
.
Teste de hipótese e o teste-z
Fazer um teste de hipótese [3-5] corresponde, em linhas gerais, à calcular a probabilidade de a sua amostra satisfazer uma determinada hipótese e, com base nesta probabilidade determinar a validade da hipótese efetuada. Um importante conceito envolvido em testes de hipótese é o nível de significância do seu resultado.
Nível de significância
O nível de significância [4] ( ) corresponde a um limite de probabilidade para se rejeitar uma hipótese. É comum utilizar níveis de 10% (0.1), 5% (0.05) e 1% (0.01). Um teste de hipótese vai retornar a probabilidade de o resultado obtido da sua amostra ser compatível com a hipótese testada. Se esta probabilidade for inferior ao nível de significância estipulado, em linhas gerais, a hipótese é rejeitada. Por exemplo, um teste de hipótese que retorna um nível de significância de 0.01 indica que há uma chance em 100 de que a hipótese testada seja verdadeira.
) corresponde a um limite de probabilidade para se rejeitar uma hipótese. É comum utilizar níveis de 10% (0.1), 5% (0.05) e 1% (0.01). Um teste de hipótese vai retornar a probabilidade de o resultado obtido da sua amostra ser compatível com a hipótese testada. Se esta probabilidade for inferior ao nível de significância estipulado, em linhas gerais, a hipótese é rejeitada. Por exemplo, um teste de hipótese que retorna um nível de significância de 0.01 indica que há uma chance em 100 de que a hipótese testada seja verdadeira.
Um cuidado importante: em muitas áreas da ciência, incluindo a física, é comum mostrar os níveis de significância em valores de  . Neste caso, um resultado com 99% de significância em relação a uma hipótese significa que há uma probabilidade de 1% de rejeição da hipótese. Por conta disso, é importante ter claro como que é definido o valor do nível de significância (
. Neste caso, um resultado com 99% de significância em relação a uma hipótese significa que há uma probabilidade de 1% de rejeição da hipótese. Por conta disso, é importante ter claro como que é definido o valor do nível de significância ( ou
ou  ). Mais importante ainda é saber interpretar o que está sendo apresentado.
). Mais importante ainda é saber interpretar o que está sendo apresentado.
Em física, em particular em física nuclear e de partículas, é comum apresentar valores de significância em número de sigmas ( ). Por exemplo, esse resultado tem
). Por exemplo, esse resultado tem 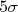 de significância. Essa significância, em números de sigma, é obtida pressupondo que a função densidade de probabilidade da grandeza estudada é uma gaussiana de desvio padrão
de significância. Essa significância, em números de sigma, é obtida pressupondo que a função densidade de probabilidade da grandeza estudada é uma gaussiana de desvio padrão  . Por exemplo, em uma gaussinana, a probabilidade de encontrarmos um valor entre
. Por exemplo, em uma gaussinana, a probabilidade de encontrarmos um valor entre 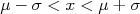 , sendo
, sendo 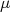 o valor médio da gaussiana, é de aproximadamente 68% (ver figura 4). Neste caso, quando falamos que o resultado tem
o valor médio da gaussiana, é de aproximadamente 68% (ver figura 4). Neste caso, quando falamos que o resultado tem 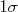 de significância, temos implícito que
de significância, temos implícito que 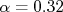 . Um resultado de
. Um resultado de 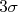 de significância indica que
de significância indica que 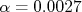 .
.
Figura 4 - Níveis de significância em uma gaussiana.
Para converter de número de  para
para  , e vice-versa, define-se a função de probabilidade acumulada de uma gaussiana como sendo:
, e vice-versa, define-se a função de probabilidade acumulada de uma gaussiana como sendo:
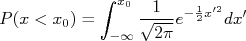
Ou seja, a probabilidade de se obter um valor menor que 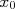 para uma F.D.P. gaussiana de média zero e desvio padrão 1. Neste caso,
para uma F.D.P. gaussiana de média zero e desvio padrão 1. Neste caso, 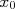 equivale ao número de
equivale ao número de  , ou seja,
, ou seja, 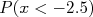 é a probabilidade de
é a probabilidade de 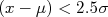 em uma gaussiana qualquer. O gráfico da função de probabilidade acumulada para uma gaussiana é mostrado na figura 5 e é uma função universal. Encontra-se facilmente páginas na internet com calculadoras para esta função, por ser muito utilizada.
em uma gaussiana qualquer. O gráfico da função de probabilidade acumulada para uma gaussiana é mostrado na figura 5 e é uma função universal. Encontra-se facilmente páginas na internet com calculadoras para esta função, por ser muito utilizada.
Figura 5 - Probabilidade acumulada para uma função gaussiana.
Na tabela 1 mostramos alguns valores de probabilidade acumulada para referência, por serem, em geral, os mais utilizados.
Tabela 1 - Probabilidade acumulada de uma gaussiana.
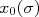 |
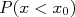 |
| -4 | 0.000032 |
| -3 | 0.00135 |
| -2 | 0.02275 |
| -1 | 0.1586 |
| 0 | 0.5000 |
| 1 | 0.8413 |
| 2 | 0.9772 |
| 3 | 0.9986 |
| 4 | 0.9999 |
Por exemplo, para grandes descobertas científicas, como a do bóson de Higgs, utiliza-se 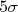 como nível de significância. Este nível de significância indica que há uma chance em 1,744,278 de que a observação nos dados analisados no LHC seja apenas uma flutuação estatística do fundo e que não exista nenhum novo bóson. Em física de partículas é comum adotar uma significância de
como nível de significância. Este nível de significância indica que há uma chance em 1,744,278 de que a observação nos dados analisados no LHC seja apenas uma flutuação estatística do fundo e que não exista nenhum novo bóson. Em física de partículas é comum adotar uma significância de 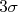 como uma interpretação para uma observação de um fenômeno e
como uma interpretação para uma observação de um fenômeno e 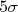 como o nível necessário para fazer um anúncio de uma descoberta. Se você rever os anúncios do bóson de Higgs no LHC perceberá que em 2010 eles fizeram uma observação e que, em 2012, anunciaram uma descoberta. Justamente por conta do nível de significância.
como o nível necessário para fazer um anúncio de uma descoberta. Se você rever os anúncios do bóson de Higgs no LHC perceberá que em 2010 eles fizeram uma observação e que, em 2012, anunciaram uma descoberta. Justamente por conta do nível de significância.
No dia a dia é comum utilizar 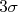 , que equivale a um valor de
, que equivale a um valor de 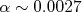 , ou seja, há uma chance em quase 400 da hipótese testada ser falsa.
, ou seja, há uma chance em quase 400 da hipótese testada ser falsa.
A escolha do nível de significância é importante porque estabelece o nível de rigor no teste de hipótese. Mais importante ainda é sempre relatar qual foi o nível de significância obtido na sua análise.
Mais a frente mostraremos alguns exemplos de como utilizar esta função na prática.
Teste de uma cauda ou duas caudas
Em um teste de hipótese estabelece-se um nível de significância  que é um valor de probabilidade de a sua hipótese ser falsa. Se a F.D.P. da sua grandeza é simétrica em relação ao valor verdadeiro há três hipóteses estatísticas que dão o mesmo valor de
que é um valor de probabilidade de a sua hipótese ser falsa. Se a F.D.P. da sua grandeza é simétrica em relação ao valor verdadeiro há três hipóteses estatísticas que dão o mesmo valor de  . Duas delas correspondem a testes de uma cauda [6], quando olhamos essencialmente a probabilidade de o resultado assumir um valor maior (ou menor) que um certo valor e uma dessas hipóteses corresponde a um teste de duas caudas [6] ou seja, a probabilidade de o resultado estar em um intervalo simétrico em torno do valor verdadeiro. A escolha de qual teste é feito depende da hipótese a ser testada.
. Duas delas correspondem a testes de uma cauda [6], quando olhamos essencialmente a probabilidade de o resultado assumir um valor maior (ou menor) que um certo valor e uma dessas hipóteses corresponde a um teste de duas caudas [6] ou seja, a probabilidade de o resultado estar em um intervalo simétrico em torno do valor verdadeiro. A escolha de qual teste é feito depende da hipótese a ser testada.
No teste de uma cauda, o nível de significância é referente à probabilidade de o resultado ser maior (ou menor) que um determinado valor. Em um teste de uma cauda,  corresponde à área da curva em um dos lados apenas da distribuição, como mostrado nas figuras 1 ou 2. Por exemplo, um teste de significância de uma cauda com nível de significância de 0.05 para a cauda da direita significa que há uma probabilidade de 0.05 de o seu resultado ser maior que um determinado valor.
corresponde à área da curva em um dos lados apenas da distribuição, como mostrado nas figuras 1 ou 2. Por exemplo, um teste de significância de uma cauda com nível de significância de 0.05 para a cauda da direita significa que há uma probabilidade de 0.05 de o seu resultado ser maior que um determinado valor.
Em um teste de duas caudas, o nível de significância é referente à probabilidade de o resultado estar distante do valor verdadeiro nas duas direções, simetricamente, como mostra a figura 3. Por exemplo, um teste de duas caudas com significância de 0.05 indica que há uma probabilidade de 0.025 de o seu resultado estar distante da média em uma direção e 0.025 dele estar distante da média na outra direção.
A escolha se o teste a ser feito é de uma cauda ou duas depende da hipótese a ser testada.
A escolha da hipótese
Antes de se fazer um teste de significância, deve-se estabelecer as hipóteses que serão testadas. Em geral escolhe-se duas hipóteses, a principal (ou hipótese nula, no jargão, 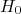 ) e uma hipótese contrária à principal (ou hipótese altenativa,
) e uma hipótese contrária à principal (ou hipótese altenativa, 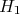 ). Em geral, a hipótese
). Em geral, a hipótese 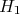 ajuda a definir se o teste é de uma cauda ou duas. Alguns exemplos:
ajuda a definir se o teste é de uma cauda ou duas. Alguns exemplos:
A aceleração obtida é compatível com a da gravidade medida pelo IAG? Neste caso a hipótese principal é 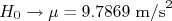 e a hipótese alternativa é
e a hipótese alternativa é 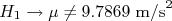 .
.
O valor obtido pelo meu grupo (1) é o mesmo que o obtido pelo outro grupo (2)? Neste caso, a hipótese principal é 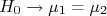 e a hipótese alternativa é
e a hipótese alternativa é 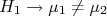 .
.
Uma vez escolhida a hipótese a ser testada, devemos escolher o teste de hipótese que será realizado. Há vários testes disponíveis e a escolha de qual teste é o mais adequado depende do tipo de amostra que temos e do nosso conhecimento da F.D.P. desta amostra.
O teste-z
O teste-z é um teste de hipótese para um valor médio de uma amostra de tamanho 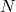 que tenha uma F.D.P. gaussiana e quando se conhece o desvio padrão verdadeiro da F.D.P. da grandeza amostrada
que tenha uma F.D.P. gaussiana e quando se conhece o desvio padrão verdadeiro da F.D.P. da grandeza amostrada 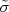 . Na pratica, quase nunca se conhece o valor verdadeiro do desvio padrão da F.D.P de uma grandeza. Ele é geralmente estimado a partir da própria amostra utilizando a expressão:
. Na pratica, quase nunca se conhece o valor verdadeiro do desvio padrão da F.D.P de uma grandeza. Ele é geralmente estimado a partir da própria amostra utilizando a expressão:
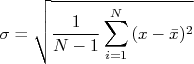
Então, à rigor, o teste-z nunca pode ser utilizado. Neste caso, deve-se utilizar o teste-t de Student [7], que veremos em momento oportuno. Contudo, na medida em que número de dados da amostra aumenta, o teste-t converge para o teste-z. Tipicamente uma amostra com tamanho maior que 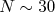 é grande o suficiente para utilizar o teste-z. Em laboratórios didáticos este número acaba sendo ainda mais relaxado para
é grande o suficiente para utilizar o teste-z. Em laboratórios didáticos este número acaba sendo ainda mais relaxado para 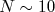 como um compromisso de se ganhar em didática com uma pequena perda de precisão estatística.
como um compromisso de se ganhar em didática com uma pequena perda de precisão estatística.
O teste-z consiste em calcular uma variável  que tenha uma F.D.P. gaussiana de média 0 e desvio padrão 1. Esta variável
que tenha uma F.D.P. gaussiana de média 0 e desvio padrão 1. Esta variável  é equivalente ao nível de significância em termos de número de
é equivalente ao nível de significância em termos de número de  para uma gaussiana.
para uma gaussiana.
A importância de se conhecer o desvio padrão verdadeiro da amostra surge quando se calcula o valor  . No cálculo de
. No cálculo de  , em geral, subtrai-se a hipótese do valor a ser testado e divide-se pelo desvio padrão do mesmo. Se for conhecido o valor verdadeiro desse desvio padrão, a F.D.P. da variável
, em geral, subtrai-se a hipótese do valor a ser testado e divide-se pelo desvio padrão do mesmo. Se for conhecido o valor verdadeiro desse desvio padrão, a F.D.P. da variável  é uma gaussiana de média 0 e desvio padrão 1. Se o desvio padrão for estimado a partir da amostra de dados, a F.D.P. da variável
é uma gaussiana de média 0 e desvio padrão 1. Se o desvio padrão for estimado a partir da amostra de dados, a F.D.P. da variável  não é mais gaussiana e sim uma F.D.P. de Student (a menos do limite de uma amostra grande, como discutido anteriormente).
não é mais gaussiana e sim uma F.D.P. de Student (a menos do limite de uma amostra grande, como discutido anteriormente).
A melhor forma de explicar o teste-z é através de exemplos. Vamos fazer alguns, passo a passo.
Exemplo 1 - Comparando um resultado a uma expectativa
Foi realizado um experimento onde mediu-se a aceleração de um corpo em queda livre. Foram realizadas 30 medidas de aceleração e a análise estatística mostrou que o valor médio dessa amostra é 9.746 m/s2 com desvio padrão de 0.12 m/s2. A incerteza do valor médio, por conta disso é 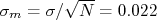 . Este valor é compatível com o valor tabelado do IAG para a aceleração da gravidade, que vale 9.7864 m/s2?
. Este valor é compatível com o valor tabelado do IAG para a aceleração da gravidade, que vale 9.7864 m/s2?
O primeiro passo é identificar a hipótese nula 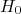 a ser testada. Esta hipótese é simplesmente
a ser testada. Esta hipótese é simplesmente  . Queremos testar esta hipótese contra o valor médio da aceleração obtida das 30 medidas. A hipótese alternativa,
. Queremos testar esta hipótese contra o valor médio da aceleração obtida das 30 medidas. A hipótese alternativa, 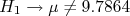 , sugere o uso de um teste de duas caudas.
, sugere o uso de um teste de duas caudas.
O segundo passo é definir o nível de significância para rejeitar esta hipótese. Isso depende de quão rigoroso você quer ser na rejeição da sua hipótese. Vamos adotar 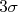 de significância.
de significância.
A F.D.P. do valor médio da aceleração medida é assumida como sendo uma gaussiana de média 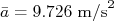 e desvio padrão
e desvio padrão 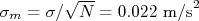 . A variável
. A variável  , que tenha F.D.P. com média zero e desvio padrão 1 é, neste caso:
, que tenha F.D.P. com média zero e desvio padrão 1 é, neste caso:
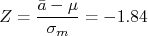
De acordo com o nível de significância de 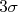 não podemos rejeitar a hipótese de que o nosso valor médio é compatível com a aceleração da gravidade pois
não podemos rejeitar a hipótese de que o nosso valor médio é compatível com a aceleração da gravidade pois  . Para este valor de
. Para este valor de 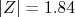 há uma chance em aproximadamente 150 desta diferença ser uma flutuação estatística, para qualquer um dos lados. A conclusão deste teste é que não há evidências suficientes que sugiram que a aceleração medida no laboratório seja diferente da aceleração da gravidade medida no IAG em uma significância de
há uma chance em aproximadamente 150 desta diferença ser uma flutuação estatística, para qualquer um dos lados. A conclusão deste teste é que não há evidências suficientes que sugiram que a aceleração medida no laboratório seja diferente da aceleração da gravidade medida no IAG em uma significância de 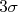 .
.
Exemplo 2 - Comparando dois resultados experimentais
Neste exemplo vamos fazer a comparação entre dois resultados experimentais. Note que o teste-z só é válido se conhecermos o desvio padrão das F.D.P. de ambas medidas, caso contrário devemos utilizar o teste-t. A menos que os desvios padrão sejam estimados de amostras muito grandes de dados.
No nosso exemplo, um grupo mediu a aceleração de queda de um número razoavelmente grande de dados e obteve 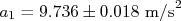 . Outro grupo, com outra amostra igualmente grande, obteve
. Outro grupo, com outra amostra igualmente grande, obteve 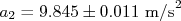 . Os dois valores são compatíveis em um nível de significância de
. Os dois valores são compatíveis em um nível de significância de 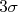 ?
?
Neste caso, a hipótese nula é 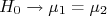 ou, reescrevendo,
ou, reescrevendo, 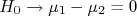 . Novamente, a hipótese alternativa,
. Novamente, a hipótese alternativa, 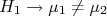 , sugere um teste de duas caudas. Se a hipótese nula for válida, a F.D.P. da diferença entre as duas medidas deve ser uma gaussiana de média 0 e desvio padrão
, sugere um teste de duas caudas. Se a hipótese nula for válida, a F.D.P. da diferença entre as duas medidas deve ser uma gaussiana de média 0 e desvio padrão 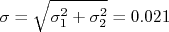 (simples propagação de incertezas). Neste caso, a variável
(simples propagação de incertezas). Neste caso, a variável  que tem F.D.P. com média 0 e desvio padrão 1 é calculada através de:
que tem F.D.P. com média 0 e desvio padrão 1 é calculada através de:
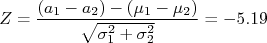
Note que o módulo de  é maior que 3, que foi o nível de significância requerido para rejeitar a hipótese nula. Neste caso, podemos dizer que a hipótese de que as acelerações são iguais foi rejeitada com um nível de significância maior do que
é maior que 3, que foi o nível de significância requerido para rejeitar a hipótese nula. Neste caso, podemos dizer que a hipótese de que as acelerações são iguais foi rejeitada com um nível de significância maior do que 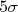 . Ou seja, a probabilidade desta diferença ser devido à flutuações estatísticas é menor do que uma em 1.8 milhão.
. Ou seja, a probabilidade desta diferença ser devido à flutuações estatísticas é menor do que uma em 1.8 milhão.
Referências
- Tratamento estatístico de dados em física experimental, O. Helene, V. Vanin, Ed. Edgard Blucher ltda.
- Fundamentos da Teoria de erros, J. H. Vuolo, Ed. Edgard Blucher ltda.
- http://en.wikipedia.org/wiki/Statistical_hypothesis_testing
- http://en.wikipedia.org/wiki/Statistical_significance
- http://www.stat.yale.edu/Courses/1997-98/101/sigtest.htm
- http://en.wikipedia.org/wiki/One-_and_two-tailed_tests
- http://en.wikipedia.org/wiki/Student%27s_t-test
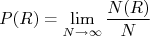
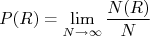
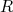 é o resultado que queremos calcular a probabilidade de ocorrência. Em geral esse resultado é definido em termos de um intervalo: qual a probabilidade de encontrar um aluno ingressante na USP entre 35 e 40 anos? Por conta disso, vamos definir a probabilidade de encontrar, em uma amostra suficientemente grande, um resultado no intervalo de
é o resultado que queremos calcular a probabilidade de ocorrência. Em geral esse resultado é definido em termos de um intervalo: qual a probabilidade de encontrar um aluno ingressante na USP entre 35 e 40 anos? Por conta disso, vamos definir a probabilidade de encontrar, em uma amostra suficientemente grande, um resultado no intervalo de  e
e 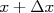 como sendo [1]:
como sendo [1]:
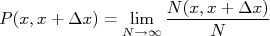
 e
e 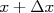 e [1]:
e [1]:
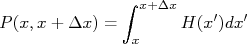
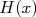 a densidade de probabilidade de ocorrer um evento
a densidade de probabilidade de ocorrer um evento  . Podemos escrever então que a função densidade de probabilidade é:
. Podemos escrever então que a função densidade de probabilidade é:
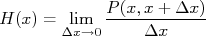
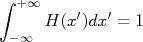
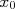 . Conhecendo-se a F.D.P. basta resolver:
. Conhecendo-se a F.D.P. basta resolver:
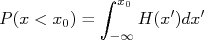
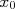 ? Da mesma forma, escrevemos:
? Da mesma forma, escrevemos:
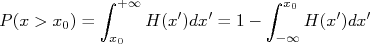
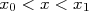 . Em termos de densidade de probabilidade a resposta é:
. Em termos de densidade de probabilidade a resposta é:
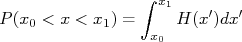
 .
.
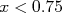 .
.
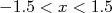 .
. ) corresponde a um limite de probabilidade para se rejeitar uma hipótese. É comum utilizar níveis de 10% (0.1), 5% (0.05) e 1% (0.01). Um teste de hipótese vai retornar a probabilidade de o resultado obtido da sua amostra ser compatível com a hipótese testada. Se esta probabilidade for inferior ao nível de significância estipulado, em linhas gerais, a hipótese é rejeitada. Por exemplo, um teste de hipótese que retorna um nível de significância de 0.01 indica que há uma chance em 100 de que a hipótese testada seja verdadeira.
) corresponde a um limite de probabilidade para se rejeitar uma hipótese. É comum utilizar níveis de 10% (0.1), 5% (0.05) e 1% (0.01). Um teste de hipótese vai retornar a probabilidade de o resultado obtido da sua amostra ser compatível com a hipótese testada. Se esta probabilidade for inferior ao nível de significância estipulado, em linhas gerais, a hipótese é rejeitada. Por exemplo, um teste de hipótese que retorna um nível de significância de 0.01 indica que há uma chance em 100 de que a hipótese testada seja verdadeira. . Neste caso, um resultado com 99% de significância em relação a uma hipótese significa que há uma probabilidade de 1% de rejeição da hipótese. Por conta disso, é importante ter claro como que é definido o valor do nível de significância (
. Neste caso, um resultado com 99% de significância em relação a uma hipótese significa que há uma probabilidade de 1% de rejeição da hipótese. Por conta disso, é importante ter claro como que é definido o valor do nível de significância ( ou
ou  ). Mais importante ainda é saber interpretar o que está sendo apresentado.
). Mais importante ainda é saber interpretar o que está sendo apresentado.  ). Por exemplo, esse resultado tem
). Por exemplo, esse resultado tem 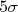 de significância. Essa significância, em números de sigma, é obtida pressupondo que a função densidade de probabilidade da grandeza estudada é uma gaussiana de desvio padrão
de significância. Essa significância, em números de sigma, é obtida pressupondo que a função densidade de probabilidade da grandeza estudada é uma gaussiana de desvio padrão  . Por exemplo, em uma gaussinana, a probabilidade de encontrarmos um valor entre
. Por exemplo, em uma gaussinana, a probabilidade de encontrarmos um valor entre 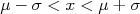 , sendo
, sendo 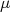 o valor médio da gaussiana, é de aproximadamente 68% (ver figura 4). Neste caso, quando falamos que o resultado tem
o valor médio da gaussiana, é de aproximadamente 68% (ver figura 4). Neste caso, quando falamos que o resultado tem 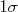 de significância, temos implícito que
de significância, temos implícito que 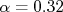 . Um resultado de
. Um resultado de 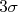 de significância indica que
de significância indica que  .
.
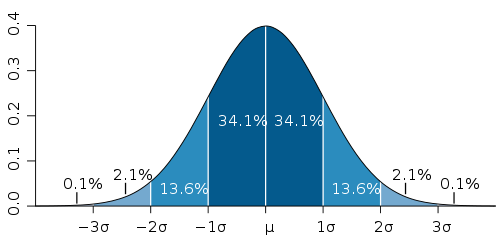
 para
para  , e vice-versa, define-se a função de probabilidade acumulada de uma gaussiana como sendo:
, e vice-versa, define-se a função de probabilidade acumulada de uma gaussiana como sendo:
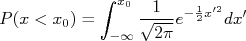
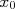 para uma F.D.P. gaussiana de média zero e desvio padrão 1. Neste caso,
para uma F.D.P. gaussiana de média zero e desvio padrão 1. Neste caso, 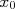 equivale ao número de
equivale ao número de  , ou seja,
, ou seja, 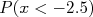 é a probabilidade de
é a probabilidade de 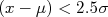 em uma gaussiana qualquer. O gráfico da função de probabilidade acumulada para uma gaussiana é mostrado na figura 5 e é uma função universal. Encontra-se facilmente páginas na internet com calculadoras para esta função, por ser muito utilizada.
em uma gaussiana qualquer. O gráfico da função de probabilidade acumulada para uma gaussiana é mostrado na figura 5 e é uma função universal. Encontra-se facilmente páginas na internet com calculadoras para esta função, por ser muito utilizada.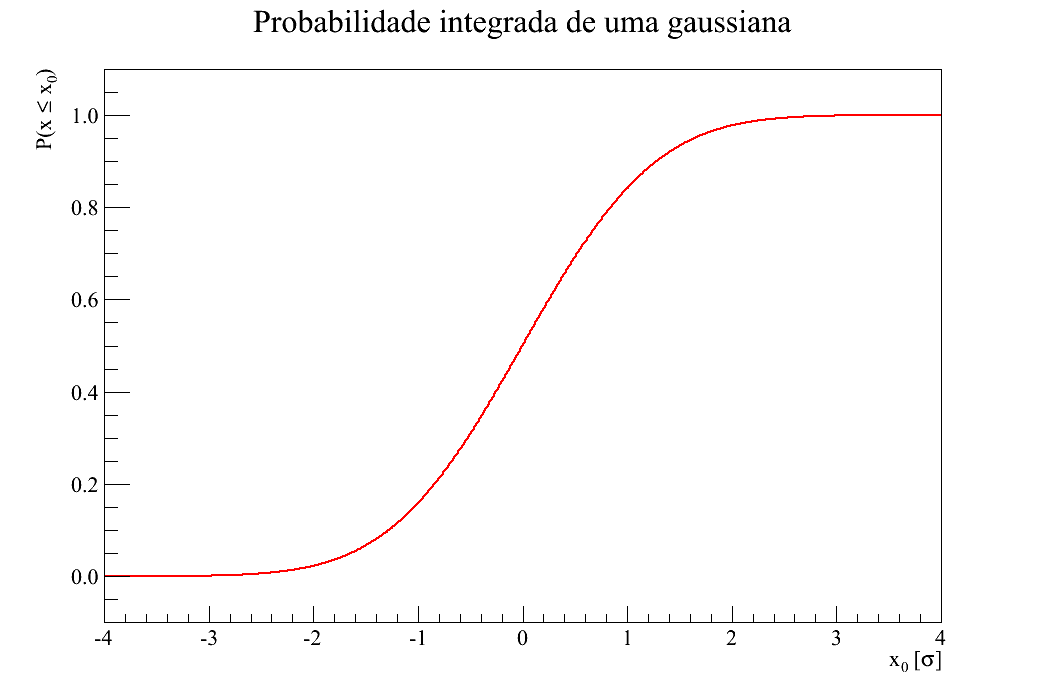
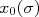
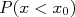
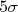 como nível de significância. Este nível de significância indica que há uma chance em 1,744,278 de que a observação nos dados analisados no LHC seja apenas uma flutuação estatística do fundo e que não exista nenhum novo bóson. Em física de partículas é comum adotar uma significância de
como nível de significância. Este nível de significância indica que há uma chance em 1,744,278 de que a observação nos dados analisados no LHC seja apenas uma flutuação estatística do fundo e que não exista nenhum novo bóson. Em física de partículas é comum adotar uma significância de 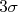 como uma interpretação para uma observação de um fenômeno e
como uma interpretação para uma observação de um fenômeno e 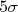 como o nível necessário para fazer um anúncio de uma descoberta. Se você rever os anúncios do bóson de Higgs no LHC perceberá que em 2010 eles fizeram uma observação e que, em 2012, anunciaram uma descoberta. Justamente por conta do nível de significância.
como o nível necessário para fazer um anúncio de uma descoberta. Se você rever os anúncios do bóson de Higgs no LHC perceberá que em 2010 eles fizeram uma observação e que, em 2012, anunciaram uma descoberta. Justamente por conta do nível de significância.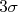 , que equivale a um valor de
, que equivale a um valor de 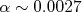 , ou seja, há uma chance em quase 400 da hipótese testada ser falsa.
, ou seja, há uma chance em quase 400 da hipótese testada ser falsa.  que é um valor de probabilidade de a sua hipótese ser falsa. Se a F.D.P. da sua grandeza é simétrica em relação ao valor verdadeiro há três hipóteses estatísticas que dão o mesmo valor de
que é um valor de probabilidade de a sua hipótese ser falsa. Se a F.D.P. da sua grandeza é simétrica em relação ao valor verdadeiro há três hipóteses estatísticas que dão o mesmo valor de  . Duas delas correspondem a testes de uma cauda [6], quando olhamos essencialmente a probabilidade de o resultado assumir um valor maior (ou menor) que um certo valor e uma dessas hipóteses corresponde a um teste de duas caudas [6] ou seja, a probabilidade de o resultado estar em um intervalo simétrico em torno do valor verdadeiro. A escolha de qual teste é feito depende da hipótese a ser testada.
. Duas delas correspondem a testes de uma cauda [6], quando olhamos essencialmente a probabilidade de o resultado assumir um valor maior (ou menor) que um certo valor e uma dessas hipóteses corresponde a um teste de duas caudas [6] ou seja, a probabilidade de o resultado estar em um intervalo simétrico em torno do valor verdadeiro. A escolha de qual teste é feito depende da hipótese a ser testada. corresponde à área da curva em um dos lados apenas da distribuição, como mostrado nas figuras 1 ou 2. Por exemplo, um teste de significância de uma cauda com nível de significância de 0.05 para a cauda da direita significa que há uma probabilidade de 0.05 de o seu resultado ser maior que um determinado valor.
corresponde à área da curva em um dos lados apenas da distribuição, como mostrado nas figuras 1 ou 2. Por exemplo, um teste de significância de uma cauda com nível de significância de 0.05 para a cauda da direita significa que há uma probabilidade de 0.05 de o seu resultado ser maior que um determinado valor.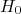 ) e uma hipótese contrária à principal (ou hipótese altenativa,
) e uma hipótese contrária à principal (ou hipótese altenativa, 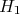 ). Em geral, a hipótese
). Em geral, a hipótese 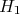 ajuda a definir se o teste é de uma cauda ou duas. Alguns exemplos:
ajuda a definir se o teste é de uma cauda ou duas. Alguns exemplos: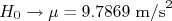 e a hipótese alternativa é
e a hipótese alternativa é 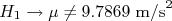 .
.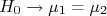 e a hipótese alternativa é
e a hipótese alternativa é 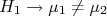 .
.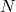 que tenha uma F.D.P. gaussiana e quando se conhece o desvio padrão verdadeiro da F.D.P. da grandeza amostrada
que tenha uma F.D.P. gaussiana e quando se conhece o desvio padrão verdadeiro da F.D.P. da grandeza amostrada 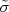 . Na pratica, quase nunca se conhece o valor verdadeiro do desvio padrão da F.D.P de uma grandeza. Ele é geralmente estimado a partir da própria amostra utilizando a expressão:
. Na pratica, quase nunca se conhece o valor verdadeiro do desvio padrão da F.D.P de uma grandeza. Ele é geralmente estimado a partir da própria amostra utilizando a expressão: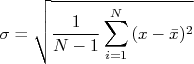
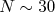 é grande o suficiente para utilizar o teste-z. Em laboratórios didáticos este número acaba sendo ainda mais relaxado para
é grande o suficiente para utilizar o teste-z. Em laboratórios didáticos este número acaba sendo ainda mais relaxado para 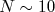 como um compromisso de se ganhar em didática com uma pequena perda de precisão estatística.
como um compromisso de se ganhar em didática com uma pequena perda de precisão estatística. que tenha uma F.D.P. gaussiana de média 0 e desvio padrão 1. Esta variável
que tenha uma F.D.P. gaussiana de média 0 e desvio padrão 1. Esta variável  é equivalente ao nível de significância em termos de número de
é equivalente ao nível de significância em termos de número de  para uma gaussiana.
para uma gaussiana.  . No cálculo de
. No cálculo de  , em geral, subtrai-se a hipótese do valor a ser testado e divide-se pelo desvio padrão do mesmo. Se for conhecido o valor verdadeiro desse desvio padrão, a F.D.P. da variável
, em geral, subtrai-se a hipótese do valor a ser testado e divide-se pelo desvio padrão do mesmo. Se for conhecido o valor verdadeiro desse desvio padrão, a F.D.P. da variável  é uma gaussiana de média 0 e desvio padrão 1. Se o desvio padrão for estimado a partir da amostra de dados, a F.D.P. da variável
é uma gaussiana de média 0 e desvio padrão 1. Se o desvio padrão for estimado a partir da amostra de dados, a F.D.P. da variável  não é mais gaussiana e sim uma F.D.P. de Student (a menos do limite de uma amostra grande, como discutido anteriormente).
não é mais gaussiana e sim uma F.D.P. de Student (a menos do limite de uma amostra grande, como discutido anteriormente). 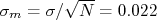 . Este valor é compatível com o valor tabelado do IAG para a aceleração da gravidade, que vale 9.7864 m/s2?
. Este valor é compatível com o valor tabelado do IAG para a aceleração da gravidade, que vale 9.7864 m/s2?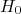 a ser testada. Esta hipótese é simplesmente
a ser testada. Esta hipótese é simplesmente  . Queremos testar esta hipótese contra o valor médio da aceleração obtida das 30 medidas. A hipótese alternativa,
. Queremos testar esta hipótese contra o valor médio da aceleração obtida das 30 medidas. A hipótese alternativa, 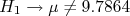 , sugere o uso de um teste de duas caudas.
, sugere o uso de um teste de duas caudas. 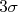 de significância.
de significância.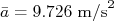 e desvio padrão
e desvio padrão 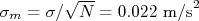 . A variável
. A variável  , que tenha F.D.P. com média zero e desvio padrão 1 é, neste caso:
, que tenha F.D.P. com média zero e desvio padrão 1 é, neste caso: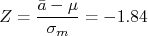
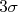 não podemos rejeitar a hipótese de que o nosso valor médio é compatível com a aceleração da gravidade pois
não podemos rejeitar a hipótese de que o nosso valor médio é compatível com a aceleração da gravidade pois  . Para este valor de
. Para este valor de 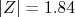 há uma chance em aproximadamente 150 desta diferença ser uma flutuação estatística, para qualquer um dos lados. A conclusão deste teste é que não há evidências suficientes que sugiram que a aceleração medida no laboratório seja diferente da aceleração da gravidade medida no IAG em uma significância de
há uma chance em aproximadamente 150 desta diferença ser uma flutuação estatística, para qualquer um dos lados. A conclusão deste teste é que não há evidências suficientes que sugiram que a aceleração medida no laboratório seja diferente da aceleração da gravidade medida no IAG em uma significância de 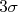 .
.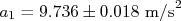 . Outro grupo, com outra amostra igualmente grande, obteve
. Outro grupo, com outra amostra igualmente grande, obteve 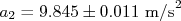 . Os dois valores são compatíveis em um nível de significância de
. Os dois valores são compatíveis em um nível de significância de 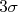 ?
?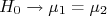 ou, reescrevendo,
ou, reescrevendo, 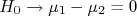 . Novamente, a hipótese alternativa,
. Novamente, a hipótese alternativa, 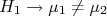 , sugere um teste de duas caudas. Se a hipótese nula for válida, a F.D.P. da diferença entre as duas medidas deve ser uma gaussiana de média 0 e desvio padrão
, sugere um teste de duas caudas. Se a hipótese nula for válida, a F.D.P. da diferença entre as duas medidas deve ser uma gaussiana de média 0 e desvio padrão 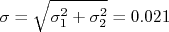 (simples propagação de incertezas). Neste caso, a variável
(simples propagação de incertezas). Neste caso, a variável  que tem F.D.P. com média 0 e desvio padrão 1 é calculada através de:
que tem F.D.P. com média 0 e desvio padrão 1 é calculada através de: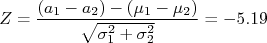
 é maior que 3, que foi o nível de significância requerido para rejeitar a hipótese nula. Neste caso, podemos dizer que a hipótese de que as acelerações são iguais foi rejeitada com um nível de significância maior do que
é maior que 3, que foi o nível de significância requerido para rejeitar a hipótese nula. Neste caso, podemos dizer que a hipótese de que as acelerações são iguais foi rejeitada com um nível de significância maior do que 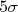 . Ou seja, a probabilidade desta diferença ser devido à flutuações estatísticas é menor do que uma em 1.8 milhão.
. Ou seja, a probabilidade desta diferença ser devido à flutuações estatísticas é menor do que uma em 1.8 milhão.