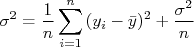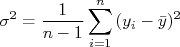Erro, incerteza e grandezas estatísticas básicas (médias e variâncias)
Sunday 06 May 2012 at 2:49 pm
Versão para impressão
É fácil observar que quando repetimos uma mesma medida, mesmo com todo cuidado do mundo e com o mesmo aparato experimental e procedimentos, o resultado obtido não é idêntico ao anterior. Isto decorre do fato de que sempre existem flutuações inerentes ao processo de medida que não podem ser eliminadas. Devemos aprender a conviver com elas e saber interpretá-las. A teoria de erros é uma parte da estatística que nos ajuda a trabalhar e compreender estas flutuações. Neste texto vamos abordar o conceito de incerteza de uma medida e aspectos introdutórios de estatística, como média, desvio padrão e desvio padrão da média.
Quando realizamos um experimento para medir algo, este "algo" é obtido da análise dos dados adquiridos no experimento realizado. Um aspecto importante para começar a desenvolver a teoria de erros, e também como motivação para se medir alguma coisa é admitir que existe um valor verdadeiro para a grandeza que queremos medir com o experimento. Contudo, este valor verdadeiro é desconhecido e, por mais precisos e acurados que sejam os experimentos realizados, o valor final obtido da análise dos seus dados está sujeito à flutuações. Neste caso, o resultado de uma medida experimental é sempre uma aproximação do valor verdadeiro da grandeza investigada.
Supondo a existência de um valor verdadeiro para uma grandeza, que chamaremos de 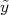 (note o til acima da letra. Este acento será sempre utilizado para representar valores verdadeiros de uma grandeza), o resultado do experimento realizado para medir esta grandeza resulta no valor
(note o til acima da letra. Este acento será sempre utilizado para representar valores verdadeiros de uma grandeza), o resultado do experimento realizado para medir esta grandeza resulta no valor  . Definimos como erro da medida realizada para esta grandeza a diferença entre o valor medido e o valor verdadeiro da mesma, ou seja:
. Definimos como erro da medida realizada para esta grandeza a diferença entre o valor medido e o valor verdadeiro da mesma, ou seja:
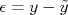
Uma vez que não conhecemos o valor verdadeiro da grandeza medida, é impossível determinar o erro de um experimento. Neste caso, deve-se utilizar de ferramentas estatísticas para definir o erro de uma medida do ponto de vista probabilístico. Sendo assim, define-se a incerteza de uma medida experimental como sendo a melhor estimativa estatística para o erro da medida efetuada.
Apesar de erro e incerteza serem conceitualmente diferentes, é bastante comum, na prática, as pessoas chamarem as incertezas obtidas em um experimento de erros. Isto não significa que o erro foi determinado. É apenas um vício de linguagem.
A teoria de erros consiste em uma formulação probabilística que tem como objetivos principais:
- Determinar o melhor valor possível para uma grandeza física a partir de um conjunto de dados obtidos de um experimento e;
- Determinar a incerteza deste melhor valor obtido.
Valor médio de uma grandeza
A partir de um conjunto de medidas estatisticamente idênticas (medidas repetidas de um mesmo experimento, com mesmos instrumentos e procedimentos):
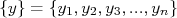
Definimos o valor médio deste conjunto de medidas como sendo:
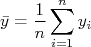
A lei dos grandes números estabelece que [1]:
Se um evento de probabilidade p é observado repetidamente em ocasiões independentes, a proporção da frequência observada deste evento em relação ao total número de repetições converge em direção a p à medida que o número de repetições se torna arbitrariamente grande.
Esta lei pode ser aplicada à situação na qual, no limite em que o número de dados no conjunto de medidas tende a infinito, o valor médio daquela amostra tende ao valor verdadeiro da grandeza, ou seja:
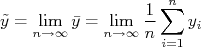
Isto é intuitivo. Na medida em que aumentamos o conjunto de dados o valor médio deste conjunto torna-se mais preciso e, consequentemente, o erro deste valor médio, menor. Por conta disso, podemos dizer que a melhor estimativa para o valor verdadeiro de uma grandeza é obtida do valor médio de um conjunto de 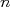 medidas idênticas para esta grandeza.
medidas idênticas para esta grandeza.
Variância e desvio padrão
Queremos agora avaliar, de uma amostra, quão dispersos estão os seus dados do valor verdadeiro. Definimos o desvio da i-ésima medida da amostra como sendo:
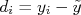
É natural pensar em usar o valor médio de 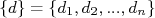 como uma forma de quantificar quão dispersos estão os dados em relação ao valor verdadeiro da grandeza medida. Por outro lado, pode-se demostrar [2] este valor médio tende a zero quando a amostra torna-se muito grande, independente de quão dispersos estejam os dados da amostra. Neste caso, define-se a variância de uma amostra como sendo a média dos desvios quadráticos, ou seja:
como uma forma de quantificar quão dispersos estão os dados em relação ao valor verdadeiro da grandeza medida. Por outro lado, pode-se demostrar [2] este valor médio tende a zero quando a amostra torna-se muito grande, independente de quão dispersos estejam os dados da amostra. Neste caso, define-se a variância de uma amostra como sendo a média dos desvios quadráticos, ou seja:
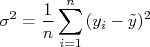
Da mesma forma que para o valor verdadeiro, o valor verdadeiro da variância associada ao processo de medidas é dada pelo:
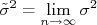
Note que para calcular a variância de uma amostra é necessário conhecer o valor verdadeiro da grandeza medida, o que não é possível. Uma boa estimativa da variância de uma amostra pode ser obtida através do cálculo do valor médio desta amostra e da expressão:
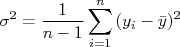
O fator 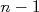 surge quando manipulamos a expressão original para a variância de modo a trocar o valor verdadeiro pelo valor médio. Veja o apêndice, no final do texto, para a dedução desta expressão.
surge quando manipulamos a expressão original para a variância de modo a trocar o valor verdadeiro pelo valor médio. Veja o apêndice, no final do texto, para a dedução desta expressão.
Definimos o desvio padrão de uma amostra como sendo a raiz quadrada da variância desta amostra, ou seja 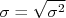 . O desvio padrão tem a mesma unidade dos valores contidos na amostra e é uma estimativa da flutuação média destes valores em torno do valor verdadeiro. Por conta disto, o desvio padrão é a quantidade mais utilizada para representar a incerteza de cada valor contido na amostra de dados.
. O desvio padrão tem a mesma unidade dos valores contidos na amostra e é uma estimativa da flutuação média destes valores em torno do valor verdadeiro. Por conta disto, o desvio padrão é a quantidade mais utilizada para representar a incerteza de cada valor contido na amostra de dados.
Desvio padrão da média
Aceitamos naturalmente que o valor médio de uma amostra é uma estimativa mais precisa do valor verdadeiro do que cada valor individualmente. Por conta disso, o erro do valor médio (consequentemente a incerteza do valor médio) deve ser menor do que o erro de cada medida individual. A variância do valor médio, então, deve ser menor que a variância das medidas individuais.
Vamos pensar em uma situação na qual o experimentador realiza o mesmo experimento todos os dias sob as mesmas condições. Em cada dia ele mede uma amostra 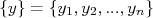 . Ao final do dia ele obtém o valor médio desta amostra. Depois de
. Ao final do dia ele obtém o valor médio desta amostra. Depois de 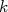 dias ele tem em mãos uma amostra de
dias ele tem em mãos uma amostra de 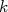 valores médios:
valores médios:
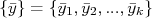
Podemos então calcular a variância desta amostra de valores médios, que é dada por:
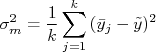
O índice 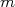 representa que a quantidade está sendo calculada na amostra de valores médios. Substituindo na expressão acima o cálculo da média de cada dia, temos:
representa que a quantidade está sendo calculada na amostra de valores médios. Substituindo na expressão acima o cálculo da média de cada dia, temos:
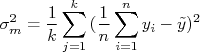
Removendo o termo 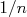 da somatória, temos:
da somatória, temos:
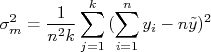
Sabendo que 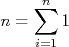 , temos que:
, temos que:
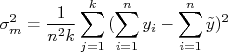
Ou seja:
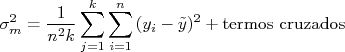
Os termos cruzados tendem a se anular. Assim, podemos reescrever a expressão acima como:
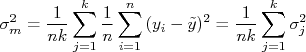
Se as amostras tomadas dia a dia tiverem a mesma variância, ou seja,  , podemos tirar a variância da somatória acima de modo que:
, podemos tirar a variância da somatória acima de modo que:
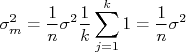
Ou seja, o desvio padrão da média está relacionado ao desvio padrão dos dados individuais através de:
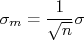
Note que o desvio padrão é uma medida da dispersão de cada medida efetuada e é, por conta disto, dependente das condições experimentais. Por outro lado, o desvio padrão da média diminui quando  aumenta. Ou seja, quanto maior for a amostra da qual se calcula a média, mais precisa esta média se torna, independentemente da flutuação dos valores individuais da amostra. Isto é compatível com a afirmação de que no limite de infinitas medidas, o valor médio da amostra torna-se o valor verdadeiro da grandeza e, consequentemente, o erro deste valor médio tende a zero.
aumenta. Ou seja, quanto maior for a amostra da qual se calcula a média, mais precisa esta média se torna, independentemente da flutuação dos valores individuais da amostra. Isto é compatível com a afirmação de que no limite de infinitas medidas, o valor médio da amostra torna-se o valor verdadeiro da grandeza e, consequentemente, o erro deste valor médio tende a zero.
Apêndice: dedução da melhor estimativa da variância de uma amostra
A variância de uma amostra é definida como:
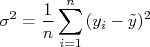
Somando e subtraindo o valor médio, temos:
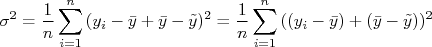
Expandindo o termo na somatória temos:
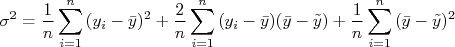
Na segunda somatória acima é nula (mostre isso como exercício). Assim temos:
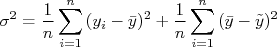
Na segunda somatória acima, podemos tirar 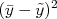 da somatória, de modo que a expressão resulta em:
da somatória, de modo que a expressão resulta em:
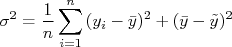
A expressão acima não é ainda independente do valor verdadeiro, como gostaríamos. Para torna-la independente, precisamos estimar a quantidade 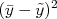 . Uma estimativa é assumir que
. Uma estimativa é assumir que 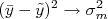 . Note que é uma estimativa e não temos como fazer muito melhor que isto. Sabendo que
. Note que é uma estimativa e não temos como fazer muito melhor que isto. Sabendo que 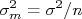 , temos que:
, temos que:
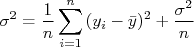
Isolando a variância na expressão acima, temos:
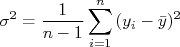
Referências
[1] http://pt.wikipedia.org/wiki/Lei_dos_grandes_n%C3%BAmeros
[2] Fundamentos da Teoria de Erros, J. H. Vuolo.
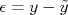
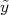 (note o til acima da letra. Este acento será sempre utilizado para representar valores verdadeiros de uma grandeza), o resultado do experimento realizado para medir esta grandeza resulta no valor
(note o til acima da letra. Este acento será sempre utilizado para representar valores verdadeiros de uma grandeza), o resultado do experimento realizado para medir esta grandeza resulta no valor  . Definimos como erro da medida realizada para esta grandeza a diferença entre o valor medido e o valor verdadeiro da mesma, ou seja:
. Definimos como erro da medida realizada para esta grandeza a diferença entre o valor medido e o valor verdadeiro da mesma, ou seja:
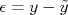
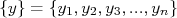
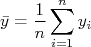
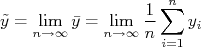
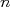 medidas idênticas para esta grandeza.
medidas idênticas para esta grandeza.
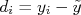
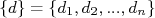 como uma forma de quantificar quão dispersos estão os dados em relação ao valor verdadeiro da grandeza medida. Por outro lado, pode-se demostrar [2] este valor médio tende a zero quando a amostra torna-se muito grande, independente de quão dispersos estejam os dados da amostra. Neste caso, define-se a variância de uma amostra como sendo a média dos desvios quadráticos, ou seja:
como uma forma de quantificar quão dispersos estão os dados em relação ao valor verdadeiro da grandeza medida. Por outro lado, pode-se demostrar [2] este valor médio tende a zero quando a amostra torna-se muito grande, independente de quão dispersos estejam os dados da amostra. Neste caso, define-se a variância de uma amostra como sendo a média dos desvios quadráticos, ou seja:
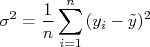
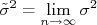
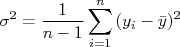
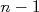 surge quando manipulamos a expressão original para a variância de modo a trocar o valor verdadeiro pelo valor médio. Veja o apêndice, no final do texto, para a dedução desta expressão.
surge quando manipulamos a expressão original para a variância de modo a trocar o valor verdadeiro pelo valor médio. Veja o apêndice, no final do texto, para a dedução desta expressão.
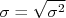 . O desvio padrão tem a mesma unidade dos valores contidos na amostra e é uma estimativa da flutuação média destes valores em torno do valor verdadeiro. Por conta disto, o desvio padrão é a quantidade mais utilizada para representar a incerteza de cada valor contido na amostra de dados.
. O desvio padrão tem a mesma unidade dos valores contidos na amostra e é uma estimativa da flutuação média destes valores em torno do valor verdadeiro. Por conta disto, o desvio padrão é a quantidade mais utilizada para representar a incerteza de cada valor contido na amostra de dados.
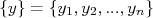 . Ao final do dia ele obtém o valor médio desta amostra. Depois de
. Ao final do dia ele obtém o valor médio desta amostra. Depois de 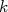 dias ele tem em mãos uma amostra de
dias ele tem em mãos uma amostra de 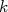 valores médios:
valores médios:
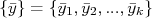
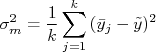
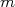 representa que a quantidade está sendo calculada na amostra de valores médios. Substituindo na expressão acima o cálculo da média de cada dia, temos:
representa que a quantidade está sendo calculada na amostra de valores médios. Substituindo na expressão acima o cálculo da média de cada dia, temos:
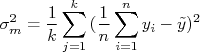
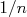 da somatória, temos:
da somatória, temos:
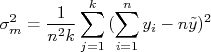
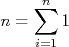 , temos que:
, temos que:
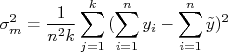
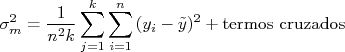
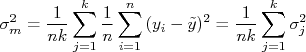
 , podemos tirar a variância da somatória acima de modo que:
, podemos tirar a variância da somatória acima de modo que:
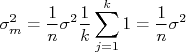
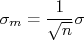
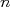 aumenta. Ou seja, quanto maior for a amostra da qual se calcula a média, mais precisa esta média se torna, independentemente da flutuação dos valores individuais da amostra. Isto é compatível com a afirmação de que no limite de infinitas medidas, o valor médio da amostra torna-se o valor verdadeiro da grandeza e, consequentemente, o erro deste valor médio tende a zero.
aumenta. Ou seja, quanto maior for a amostra da qual se calcula a média, mais precisa esta média se torna, independentemente da flutuação dos valores individuais da amostra. Isto é compatível com a afirmação de que no limite de infinitas medidas, o valor médio da amostra torna-se o valor verdadeiro da grandeza e, consequentemente, o erro deste valor médio tende a zero.
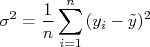
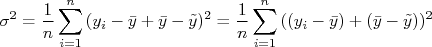
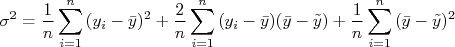
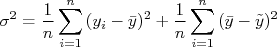
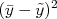 da somatória, de modo que a expressão resulta em:
da somatória, de modo que a expressão resulta em:
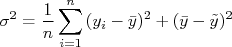
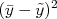 . Uma estimativa é assumir que
. Uma estimativa é assumir que 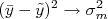 . Note que é uma estimativa e não temos como fazer muito melhor que isto. Sabendo que
. Note que é uma estimativa e não temos como fazer muito melhor que isto. Sabendo que 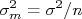 , temos que:
, temos que: