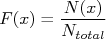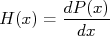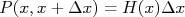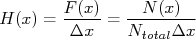Confecção de gráficos
Thursday 01 March 2012 at 3:50 pm
Este texto foi baseado nas apostilas “Introdução à interpretação gráfica de dados, gráficos e equações”, 1990, dos Profs. Fuad Saad, Paulo Yamamura e Kazuo Watanabe; “Física Geral e Experimental para Engenharia I”, 2003, dos Profs. Ewout ter Haar e Valdir Bindilati. Este texto é, também, a versão digital do capítulo da apostila de Introdução à Medidas em Física que eu e o Prof. Marcelo Munhoz escrevemos quando coordenamos a disciplina entre 2005 e aproximadamente 2007.
Versão para impressão
Introdução
Nas atividades experimentais, muitas vezes, objetiva-se estudar a maneira como uma propriedade, ou quantidade, varia com relação a uma outra quantidade, por exemplo:
“De que modo o comprimento de um pêndulo afeta o seu período?”
ou ainda:
“Como se comporta a força de atrito entre duas superfícies relativamente à força normal exercida por uma superfície sobre a outra?”
Tais questões podem ser estudadas e mais bem respondidas, muitas vezes, através de métodos gráficos evidenciando, dessa forma, a dependência de uma grandeza em relação à outra. Neste capítulo apresentaremos os principais tipos de gráficos disponíveis bem como técnicas para a sua confecção. Apresentaremos também alguns métodos de análise gráfica de dados de forma a poder extrair informações e interpretar resultados experimentais.
Tipos de gráficos
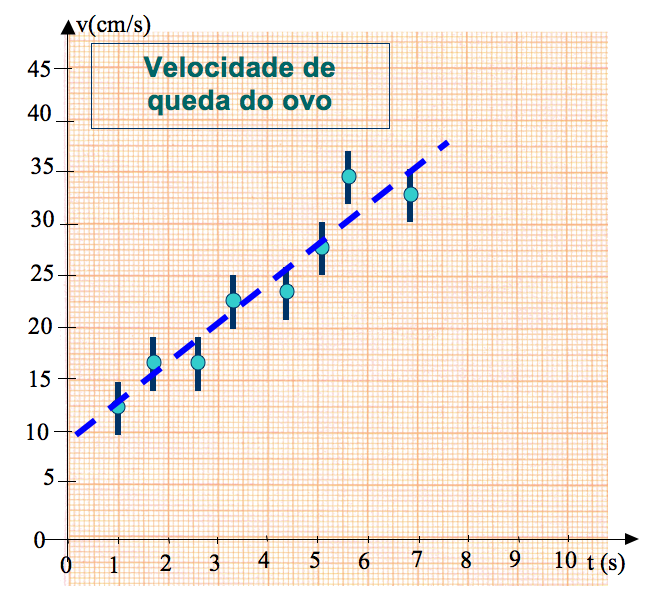
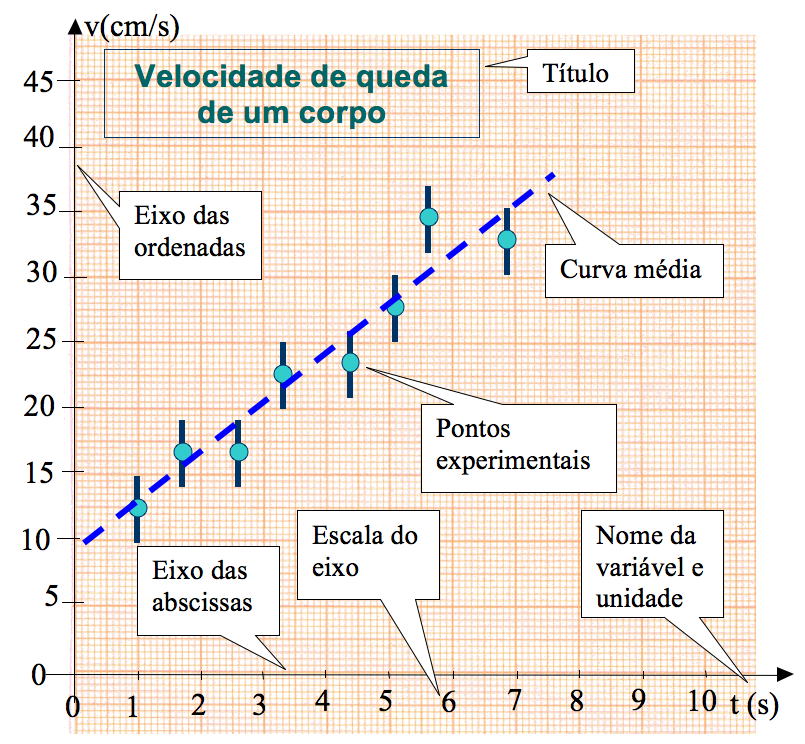
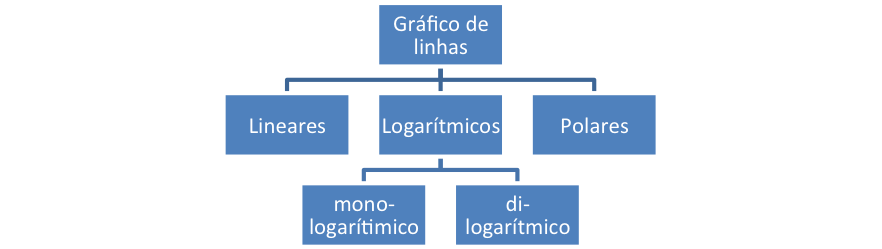
Os gráficos, de modo geral, podem ser classificados em cinco tipos básicos, conforme o esquema apresentado na figura 1. Dependendo do tipo de análise a ser realizada um tipo de gráfico torna-se mais adequado que outro. Nos trabalhos experimentais em Ciências são frequentemente utilizados gráficos do tipo diagrama, ou linha, conforme o apresentado na figura 2. Nesse gráfico é mostrado o comportamento de uma grandeza física, nesse caso a velocidade de um corpo, em função do tempo. Pode-se perceber facilmente que a velocidade aumenta com o passar do tempo. A grande vantagem de análises gráficas é a interpretação direta e fácil de dados experimentais. A linha tracejada, nesse caso, representa o comportamento médio dos dados obtidos e representa a tendência dos dados.
Figura 1 - Principais tipos de gráficos.
Figura 2 - Exemplo de gráfico linear. Nesse gráfico, os pontos correspondem às medidas experimentais e a linha representa o comportamento médio.
Confecção de gráficos
Quando são realizados experimentos, os dados são adquiridos, geralmente, de dois modos:
No primeiro modo, quer-se examinar a dependência de uma grandeza em relação à outra, como, por exemplo, os dados apresentados na figura 2. Nesse caso, mede-se a velocidade do corpo em instantes consecutivos de tempo e analisa-se como a velocidade depende do tempo. Em medidas desse tipo, costuma-se denominar de variável independente aquela que se varia, nesse caso, o tempo. A grandeza na qual se quer estudar a dependência, nesse caso a velocidade, é denominada de variável dependente.
No segundo caso, o mesmo experimento é repetido muitas vezes nas mesmas condições e, em cada um desses experimentos, repete-se a medida de uma determinada grandeza. Nesse caso, querem-se estudar as variações de medidas devido às incertezas experimentais. Um caso típico é a medida do período de oscilação de um pêndulo simples. Dependendo dos instrumentos utilizados, a medida simples de um único período resulta, geralmente, em incertezas experimentais elevadas que podem ser minimizadas através da repetição do experimento muitas vezes. Assim, a medida final seria a média aritmética de todas as medidas efetuadas.
Em ambas as situações costuma-se organizar os dados em tabelas. Essas tabelas podem-se tornar demasiadamente longas e de difícil leitura. A representação desses dados em forma gráfica mostra, de forma mais clara, as propriedades das grandezas medidas. O gráfico mostra, igualmente, prováveis erros experimentais e permite realizar interpolações e extrapolações de modo visível e fácil.
No primeiro exemplo pode-se visualizar graficamente o comportamento da velocidade em função do tempo através de um gráfico de linhas. No segundo caso, contudo, a melhor visualização gráfica é feita através de um histograma. Nesse tipo de gráfico é muito simples obter grandezas como média e desvio padrão das medidas.
Antes de abordar os tipos de gráfico acima, devemos estabelecer algumas regras gerais de confecção de gráficos. Essas regras se aplicam a quase todos os tipos disponíveis.
Regras gerais para confecção de gráficos
A construção de gráficos, quando feita sob regras universais, facilita significativamente a sua interpretação. Nesse sentido, regras rígidas (como regras de sintaxe de uma linguagem qualquer) são adotadas no mundo científico e tecnológico.
Todo gráfico é composto dos seguintes itens:
- Título e legenda do gráfico;
- Eixos das variáveis com os nomes das variáveis, escalas e unidades;
- Dados experimentais e incertezas;
- Funções teóricas ou curvas médias (esse último item é opcional e, dependendo das circunstâncias, pode ser omitido);
A figura 3 mostra os principais componentes de um gráfico.
Figura 3 - Componentes típicos de um gráfico científico padrão.
Título e legenda do gráfico
Todo gráfico dever ter um título. Geralmente, o título do gráfico é colocado na parte superior do gráfico, em destaque. Títulos do tipo “gráfico de velocidade vs. tempo" são redundantes e não fornecem informação necessária para o entendimento do mesmo.
Caso o gráfico seja inserido dentro de um texto, o mesmo deve ser acompanhado de uma legenda, logo abaixo do gráfico, numerada, que explique de forma sucinta o seu conteúdo. No caso da presença de uma legenda, o título do gráfico torna-se opcional, já que a legenda acaba suprindo o leitor de informação suficiente para o entendimento do gráfico.
Eixos, escalas e unidades
Os eixos de um gráfico devem ser explicitamente desenhados. Cada um dos eixos deve conter o nome (ou símbolo) da variável representada, a escala de leitura e a unidade correspondente.
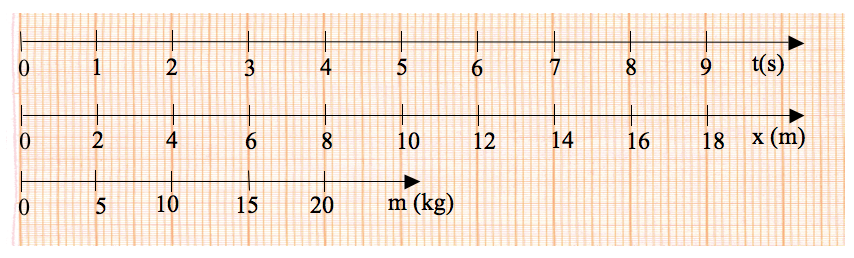
A escolha da escala utilizada deve ser tal que represente bem o intervalo medido para a variável correspondente. A regra prática para definir a escala a ser utilizada consiste em dividir a faixa de variação da variável a ser graficada pelo número de divisões principais disponíveis. Toma-se, então, um arredondamento para um valor superior e de fácil leitura. Esses valores são, em geral, 1, 2, 5 ou múltiplos/sub-múltiplos de 10 desses valores (10; 20; 500; 0,5; etc.). A figura 4 mostra alguns exemplos de escalas do eixo de um gráfico. Múltiplos de 3 são de difícil leitura e devem ser evitados.
Figura 4 - Alguns exemplos de formas CORRETAS de desenhar eixos em um gráfico.
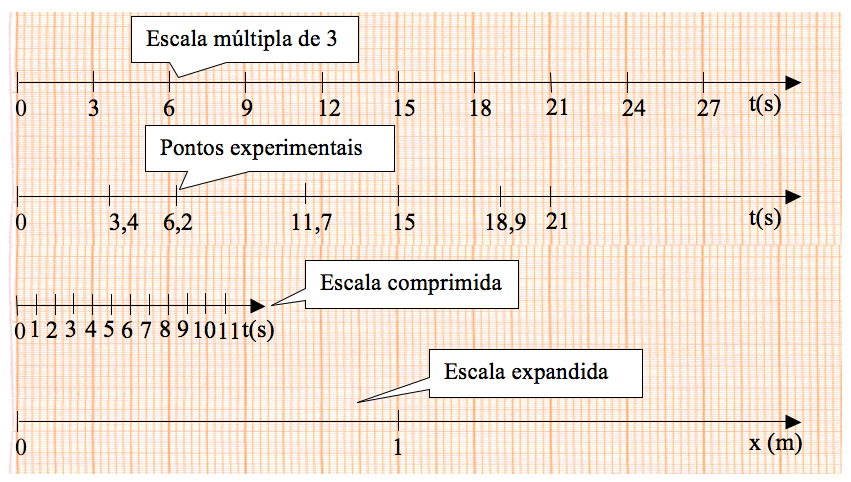
As escalas de um gráfico não precisam começar na origem (0, 0). Elas devem abranger a faixa de variação que você quer representar. É conveniente que os limites da escala correspondam a um número inteiro de divisões principais. Indique os valores correspondentes às divisões principais abaixo (eixo-x) ou ao lado (eixo-y) da escala utilizando números legíveis. As unidades devem ser escolhidas de maneira a minimizar o número de dígitos utilizados na divisão principal (ver a terceira escala, de cima para baixo, na figura 4. Nesse caso, utilizou-se a escala de quilo-grama). Uma regra prática é utilizar no máximo 3 dígitos para representar esses valores. Pode-se também fazer o uso de potências de 10 na expressão das unidades para simplificar a escala.
Ao traçar os eixos em papel gráfico comum, não use a escala marcada no papel pelo fabricante. Você é quem define a escala. Também evite usar os eixos nas margens do papel. Desenhe os seus próprios eixos. Na figura 5 são mostradas algumas formas INCORRETAS de desenhar eixos de gráfico. Um erro muito comum é colocar nos eixos os valores medidos para cada variável. Esse é um erro MUITO grosseiro que torna o gráfico ilegível.
Figura 5 - Algumas formas INCORRETAS de desenhar eixo em um gráfico.
Por fim, escreva o nome (ou símbolo) da variável correspondente ao eixo e a unidade para leitura dos valores entre parêntesis (s, kg, 105 N/m2, etc.).
No final das contas, o melhor critério para desenhar um eixo de um gráfico é o bom-senso. O teste final para saber se o eixo utilizado é adequado é a escolha aleatória de um ponto qualquer. O leitor deve ser capaz de identificar rapidamente o valor correspondente desse ponto através da leitura do eixo no gráfico.
Representação de dados
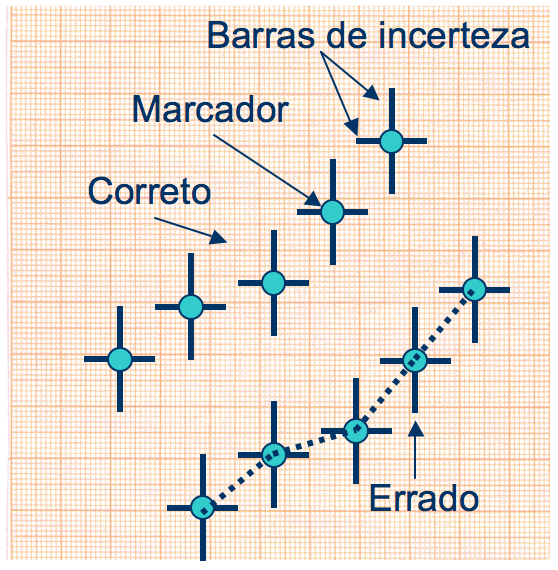
Assinale no gráfico a posição dos pontos experimentais: use marcas bem visíveis (em geral círculos cheios). NUNCA indique as coordenadas dos pontos graficados no eixo. Coloque as barras de incerteza nos pontos, se for o caso. Se as incertezas são menores que o tamanho dos pontos, indique isso na legenda.
NUNCA LIGUE OS PONTOS. São raras as exceções onde isto é realmente necessário. A figura 6 mostra como desenhar os pontos experimentais em um gráfico.
Às vezes, dependendo da análise a ser realizada com os dados, é necessário o desenho de curvas médias ou funções teóricas. Essas curvas têm como utilidade permitir a extrapolação e/ou interpolação de pontos, bem como a comparação entre os dados experimentais e uma previsão teórica. Esse ponto será discutido em detalhes adiante.
Figura 6 - Representação de pontos experimentais em um gráfico. Indique as barras de incerteza (se for o caso) em cada ponto nos eixos x e y.
Gráficos de linhas
Gráficos de linhas são normalmente utilizados para representar a dependência de uma grandeza em relação à outra, como o gráfico apresentado na figura 2 que mostra a dependência com o tempo da velocidade de queda de um ovo. São muitos os tipos de gráficos de linhas que podem ser construídos. Dentre os vários se destacam três tipos comumente utilizados, conforme representado na figura 7.
Figura 7 - Principais tipos de gráficos de linhas utilizados no meio científico.
A escolha do tipo de gráfico está relacionada com os objetivos que se pretende alcançar. Um dos fatores que pode fornecer a ajuda na escolha é analisar a variação dos dados adquiridos. Por exemplo, uma grandeza que varia entre 10 Hz e 100 kHz (100000 Hz) torna-se impossível de ser graficada de forma eficiente em um gráfico linear, devido à grande variação entre um extremo e outro. Nesse caso, gráficos logarítmicos são mais adequados para representar dados desse tipo.
Escalas lineares
Gráficos em escalas lineares são os mais simples de serem realizados. Como o próprio nome diz, gráficos em escalas lineares são aqueles nos quais ambos os eixos (x e y) são lineares, ou seja, a escala representada no eixo é diretamente proporcional à distância do ponto em relação à origem do eixo. Gráficos em escalas lineares são desenhados normalmente em papéis milimetrados, conforme mostra a figura 2.
Escalas logarítmicas
Em muitas situações é comum fazer gráficos de grandezas onde a dependência com uma outra variável é dada por expressões do tipo:
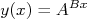 ou
ou 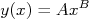
Nesse caso, dependendo das constantes A e B, a grandeza y(x) pode variar muitas ordens de grandeza a partir de pequenas variações de x. É claro que, nesse caso, mudanças de variáveis podem ser realizadas para tornar as equações acima retas. Em geral, as mudanças de variáveis mais comuns envolvem funções logarítmicas. No passado, o cálculo de logaritmos era bastante trabalhoso e envolvia consulta a tabelas (ou tábuas) de logaritmos, nem sempre disponíveis. Nesse sentido, foram criados papéis gráficos especiais nos quais uma (ou ambas) das escalas é graduada logaritmicamente. A escala logarítmica é construída de tal forma que quando uma quantidade x é marcada nessa escala o comprimento (distância em relação à origem do eixo) é proporcional à log(x). Um trecho de uma escala logarítmica é mostrado na figura 8. Assim, a escala logarítmica é útil quando a mudança de variável necessária para linearizar o gráfico envolver o logaritmo de um número.
Figura 8 - Escala logarítmica (abaixo) em comparação com a escala linear (acima). A escala logarítmica é construída de tal forma que quando uma quantidade x é marcada nessa escala o comprimento (distância em relação à origem do eixo) é proporcional a log(x).
Devido à forma na qual a escala logarítmica é construída, deve-se ficar atento para algumas regras de uso:
- Não existe zero em escala logarítmica. Devido ao fato de
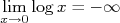 é impossível definir o valor zero na escala.
é impossível definir o valor zero na escala.
- A escala logarítmica é dividida em décadas. Cada década corresponde a uma ordem de grandeza decimal. A divisão da escala, em cada década, é idêntica de uma década para outra.
- Pelo fato da posição da escala ser proporcional a log(x) não podemos escolher qualquer escala para fazer o gráfico. A posição equivalente ao 1 na escala logarítmica da figura 8 pode ser atribuída somente a números do tipo 1; 0,1; 10; 1000; etc. Do mesmo modo, a posição 3 só pode ser atribuída a números do tipo 3; 0,3; 30; 3000; etc.
- Uma década subsequente tem que, necessariamente, possuir escala de tal forma que os números são marcados uma ordem de grandeza acima da década anterior. Por exemplo, caso a década anterior varie de 0,01 à 0,1; a década subsequente deve variar de 0,1 à 1 e assim sucessivamente.
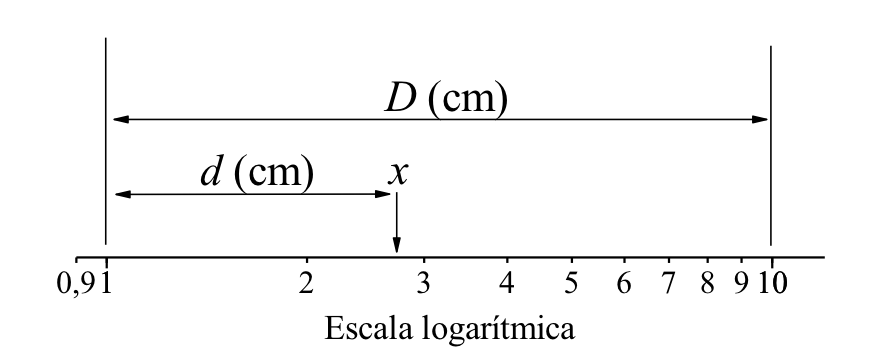
Um uso interessante para a escala logarítmica diferente de fazer gráficos é a forma simples de calcular logaritmos. Como a posição de um valor x, na escala, é proporcional a log(x), e como o tamanho de uma década corresponde a variação de 1 em logaritmos (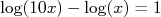 , qualquer que seja x) podemos usar essa informação para o cálculo de logaritmos. Para isso, basta medir a distância d (em centímetros) da posição de x na escala logarítmica e o tamanho da década D, conforme mostra a figura 9. Desse modo, log(x) vale:
, qualquer que seja x) podemos usar essa informação para o cálculo de logaritmos. Para isso, basta medir a distância d (em centímetros) da posição de x na escala logarítmica e o tamanho da década D, conforme mostra a figura 9. Desse modo, log(x) vale:
![\log(x)=\frac{d[cm]}{D[cm]} \log(x)=\frac{d[cm]}{D[cm]}](/~suaide/blog/pivotx/extensions/renderlatex/pictures/8a7e0d20169bfd3efb0fa072ca76cbd7.png)
Figura 9 - Cálculo de log(x) utilizando a escala logarítmica.
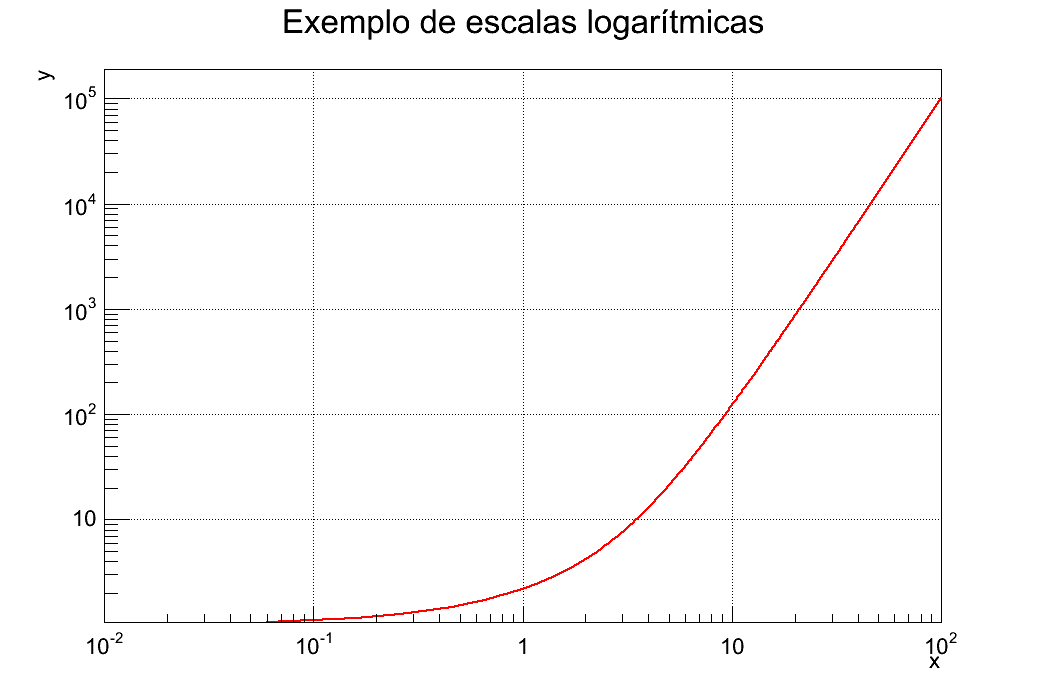
Um exemplo de um gráfico com escalas logarítmicas é mostrado na figura 10.
Figura 10 - Exemplo de gráfico com escalas logarítmicas.
Em um outro texto mostraremos como extrair informações quantitativas de gráficos, tais como coeficientes angular e linear e linearização de gráficos.
Histogramas
Vamos imaginar o seguinte experimento. Um cientista resolve medir o período de oscilação de um pêndulo. Após realizar o experimento uma única vez ele obtém um determinado valor T para o período de oscilação desse pêndulo. Contudo, após repetir o experimento várias vezes ele observa que cada experimento, mesmo que efetuado sob as mesmas condições experimentais (aquelas controladas pelo experimentador), fornece um valor diferente para o período de oscilação. Nesse caso, o experimentador conclui que o período de oscilação do pêndulo pode ser dado pela média de todas as medidas efetuadas. Contudo, outras questões podem ser igualmente importantes: como as medidas se distribuem em torno desse valor médio? O valor médio é também o valor mais provável de ser medido? Qual a probabilidade de realizar uma medida na qual o período de oscilação obtido é duas vezes maior que o valor médio?
Muitas dessas questões podem ser resolvidas através da análise estatística das medidas efetuadas. Contudo, uma ferramenta importante para análise estatística é o histograma das medidas. Um histograma é um gráfico no qual o conjunto de pontos (x, y) tem um significado específico. Um certo valor y está diretamente relacionado com a probabilidade de efetuar uma determinada medida e obter, como resultado, o valor x. Voltando ao nosso exemplo do pêndulo, a variável graficada no eixo-x poderia ser o período de oscilação enquanto que a variável no eixo-y pode ser o número de vezes que aquele determinado período foi medido pelo experimentador.
Por ter um significado específico, muitas vezes um histograma não é graficado colocando pontos nas coordenadas (x, y) de um papel milimetrado e sim através dos desenhos de barras verticais cuja altura corresponde ao valor y obtido para o ponto x.
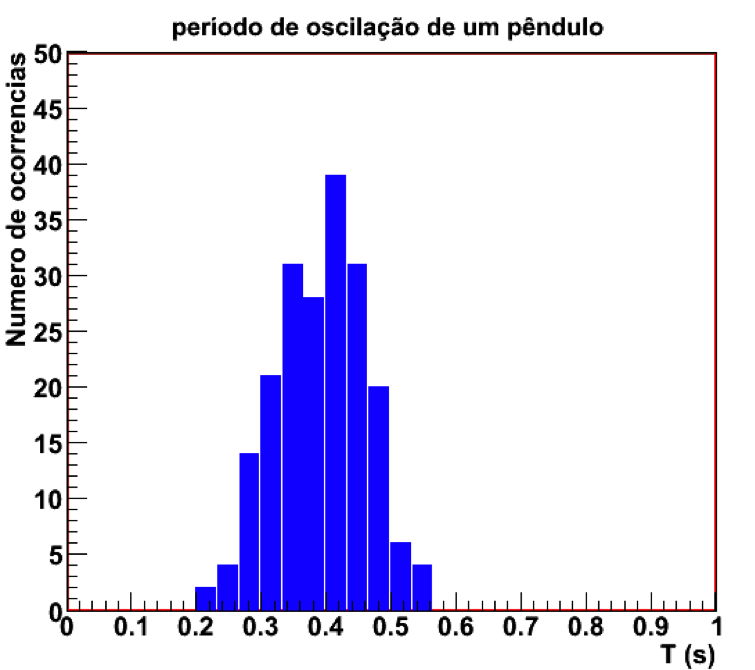
A figura 11 mostra um histograma típico para o nosso experimento fictício. Nesse caso, o experimentador realizou a mesma medida 200 vezes. Cada barra vertical no histograma corresponde a um intervalo de períodos. Por exemplo, a barra mais alta corresponde a medidas cujo período de oscilação estava entre 0,40 e 0,43 segundos. Após repetir 200 vezes o experimento, o experimentador obteve 39 medidas cujo período de oscilação do pêndulo encontrava-se nesse intervalo de tempo. Para o intervalo de tempo entre 0,50 e 0,53 segundos, o experimentador obteve somente 6 medidas nesse intervalo. Cada um desses intervalos de medidas, que corresponde a uma barra no histograma é denominado de um canal do histograma. Em geral, histogramas possuem canais cujas larguras são fixas para todo o histograma. Casos especiais de histograma possuem canais de larguras variadas, porém são mais difíceis de serem analisados.
Figura 11 - Histograma do período de oscilação de um pêndulo simples para um experimento realizado 200 vezes.
A amplitude a ser graficada em um histograma, para cada intervalo de variação da medida, depende de como esse histograma será utilizado posteriormente. É comum, contudo, utilizar uma das seguintes opções:
Histograma de número de ocorrências (N)
A amplitude do histograma, N(x), é simplesmente o número de ocorrências verificadas em cada canal do histograma cujo centro vale x. Apesar de ser o histograma mais simples de se construir, pois exige apenas a contagem do número de ocorrências, a análise do mesmo é mais trabalhosa. Por exemplo, para calcular a probabilidade de efetuar uma medida em um intervalo é necessário saber o número total de medidas utilizadas no histograma.
Histograma de freqüência de ocorrência (F)
A freqüência na qual ocorre uma determinada medida é definida como sendo a razão entre o número de ocorrências em um canal do histograma cujo centro vale x e o número total de medidas efetuada, ou seja:
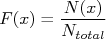
A vantagem de utilizar essa variável como amplitude do histograma é óbvia. A simples leitura da amplitude do histograma em um determinado canal, no limite de um grande número de medidas, Ntotal, tende à probabilidade de realizar uma medida no intervalo correspondente ao canal estudado. No caso mostrado na figura 11, como o experimento foi realizado 200 vezes, a freqüência de ocorrência para um dado canal é o número de contagens daquele canal, dividido por 200.
Apesar de os histogramas de ocorrências (N) e freqüências (F) serem simples de construir eles possuem algumas limitações. A maior delas é o fato das amplitudes nesses histogramas serem fortemente dependentes da largura escolhida para os canais. Caso a largura escolhida seja duas vezes maior, tanto os números de ocorrências como as freqüências serão também duas vezes maiores. Esse aspecto torna histogramas de ocorrências e freqüências difíceis de serem comparados com outros histogramas, bem como com curvas teóricas. Um terceiro tipo de histograma, definido como histograma de densidades de probabilidade, elimina essa limitação.
Histograma de densidade de probabilidades ( H )
A densidade de probabilidade é definida como sendo a razão entre a probabilidade de realizar uma medida no intervalo x e x+dx e o tamanho do intervalo, dx, no limite no qual esse intervalo é muito pequeno, ou seja:
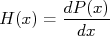
Se a densidade de probabilidade é conhecida, a probabilidade de ocorrer um resultado em um intervalo (x, x+Δx), com Δx pequeno, é, aproximadamente:
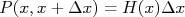
A grande vantagem de utilizar a densidade de probabilidade para montar histogramas é o fato das amplitudes em cada canal ser independente do número de medidas efetuadas bem como da largura escolhida para os canais do histograma. Experimentalmente, a densidade de probabilidade pode ser obtida como sendo a frequência de ocorrência de eventos em um canal, dividida pela largura do canal no histograma, ou seja:
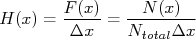
Construção de histogramas
Depois de realizadas as medidas, o experimentador tem em mãos uma tabela na qual estão listados os valores obtidos para a grandeza que se quer histogramar. Construir um histograma consiste nos seguintes passos:
- Escolher a largura dos canais do histograma, Δx.
- Escolher os centros de cada canal, tomando o cuidado que não sobrem espaços vazios entre os canais.
- Contar o número de ocorrências para cada um dos canais, N(x). Nesse ponto é possível construir o histograma de número de ocorrências. Caso uma ocorrência ocorra na borda entre dois canais, considere a ocorrência como pertencendo ao canal cujo centro possua maior valor.
- Caso queira-se construir o histograma de frequências, F(x) dividir o número de ocorrências em cada canal pelo total de medidas efetuadas.
- Caso queira-se construir o histograma de densidade de probabilidades, H(x), dividir a frequência de cada canal pela largura de cada um dos canais.
Alguns problemas ocorrem na criação do histograma, principalmente quando o número total de medidas (Ntotal) é estatisticamente pequeno.
O problema mais frequente é a escolha da largura do canal, Δx. Evidentemente, para que a densidade de probabilidade experimental seja o mais próxima possível da definição teórica, deve-se escolher Δx de tal forma a ser o menor valor possível. Entretanto, diminuindo Δx estamos também diminuindo o número de ocorrências em cada canal do histograma, correndo o risco de que, em casos extremos, ocorram canais onde não seja registrada nenhuma ocorrência.
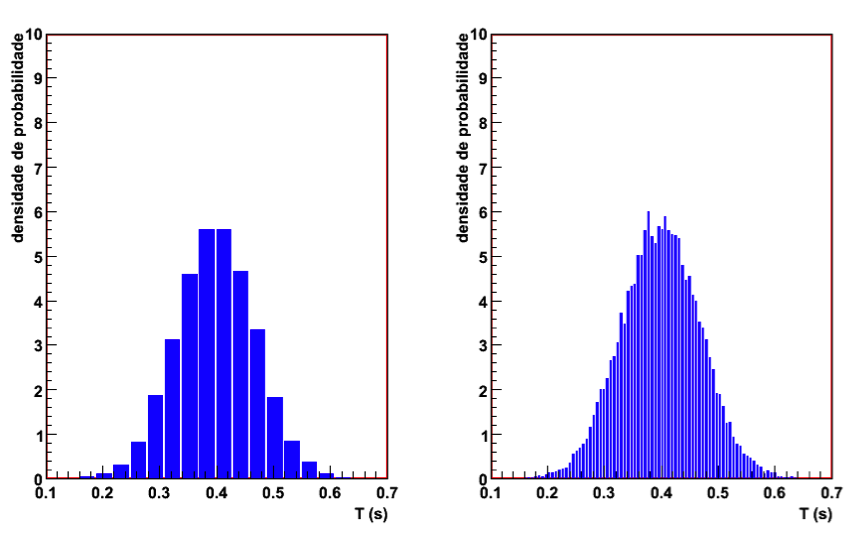
A figura 12 mostra dois histogramas onde foram realizadas 20 medidas. No histograma da esquerda, a largura do canal utilizada é cinco vezes mais larga que no histograma da direita. Note que o histograma com largura de canal menor apresenta flutuações elevadas de um canal para outro, além de haver canais onde não há ocorrências. Isso resulta em alguns canais com elevada densidade de probabilidade enquanto outros canais apresentam densidade de probabilidade nula.
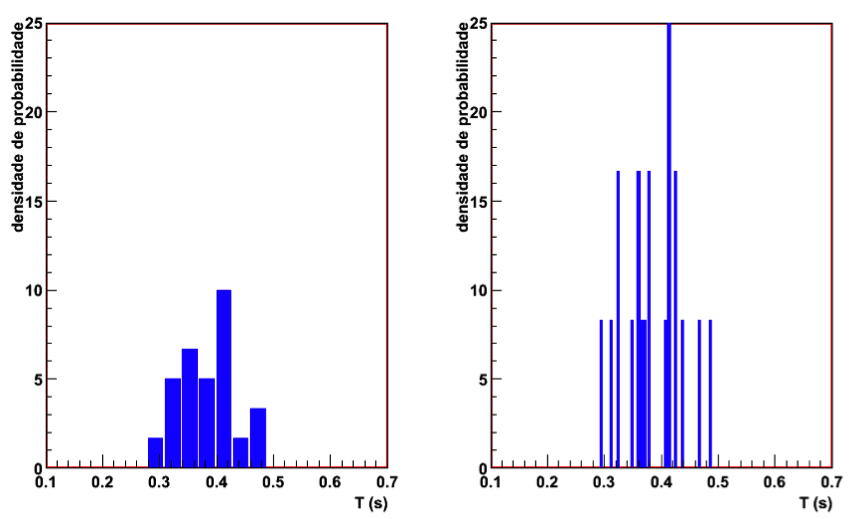
Esse fator deixa de ser um problema quando o número de medidas é bastante elevado, como mostrado na figura 13. Nesse caso, o experimento hipotético foi realizado 20 mil vezes. Note que, além do tamanho dos canais, não há diferença entre as densidades de probabilidade entre os histogramas.
Figura 13 - Histogramas de densidade de probabilidades para medidas do período de um pêndulo simples, conforme explicado na figura 12. Nesse caso, o total de medidas utilizadas para montar os histogramas (Ntotal) foi 20000.
Em muitas situações experimentais é muito difícil realizar um número elevado de medidas de tal forma que a escolha da largura dos canais no histograma possa ser arbitrariamente pequena. Como regra prática, a largura dos canais, Δx, deve ser escolhida de tal forma que o número de ocorrências, N(x), seja pelo menos 10 para os canais próximos ao valor médio das medidas. Outro fator importante é a escolha das posições centrais dos canais do histograma. Deve-se, nesse caso, escolher as posições centrais de tal forma que uma delas seja aproximadamente igual ao valor médio das medidas.
Interpretação de um Histograma
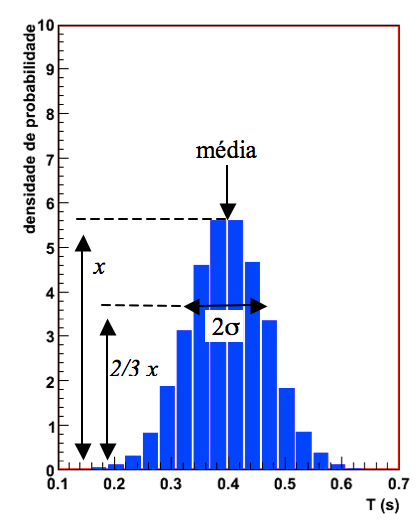
Quando medimos N vezes uma grandeza, normalmente obtemos valores diferentes para cada medida devido à incerteza estatística ou aleatória associada ao procedimento de medida. Se a incerteza é aleatória, é razoável supor que ela pode fazer com que o resultado da medida seja igualmente maior, ou menor, que o valor verdadeiro da grandeza. Portanto, esperamos que um histograma tenha uma forma simétrica em torno do valor que representa a melhor estimativa para o valor verdadeiro da medida, como podemos observar no histograma da figura 14.
Figura 14 - Obtenção de média e desvio padrão a partir da análise gráfica do histograma.
A largura do histograma deve refletir a precisão da medida, pois ela mostra o quanto as medidas variaram em torno da estimativa do valor verdadeiro. Um histograma mais largo significa uma medida menos precisa e vice-versa. Como discutido no capítulo 5 da apostila “Introdução à Teoria de Erros” de J. H. Vuolo, a melhor estimativa do valor verdadeiro de uma medida é dada pela média e a variação (ou variância) das medidas é dada pelo desvio padrão. Portanto, podemos estimar o valor da média e do desvio padrão de um conjunto de medidas a partir do seu histograma, somente observando o valor central do mesmo e a largura do histograma a, aproximadamente, 2/3 de sua altura máxima, conforme mostra a figura 14. Uma discussão mais formal sobre essa interpretação do significado do valor central e da largura de um histograma pode ser encontrada no capítulo 7 da apostila “Introdução à Teoria de Erros”.

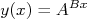 ou
ou 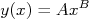

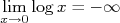 é impossível definir o valor zero na escala.
é impossível definir o valor zero na escala.
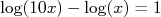 , qualquer que seja x) podemos usar essa informação para o cálculo de logaritmos. Para isso, basta medir a distância d (em centímetros) da posição de x na escala logarítmica e o tamanho da década D, conforme mostra a figura 9. Desse modo, log(x) vale:
, qualquer que seja x) podemos usar essa informação para o cálculo de logaritmos. Para isso, basta medir a distância d (em centímetros) da posição de x na escala logarítmica e o tamanho da década D, conforme mostra a figura 9. Desse modo, log(x) vale:
![\log(x)=\frac{d[cm]}{D[cm]} \log(x)=\frac{d[cm]}{D[cm]}](/~suaide/blog/pivotx/extensions/renderlatex/pictures/8a7e0d20169bfd3efb0fa072ca76cbd7.png)