O espalhamento Rutherford
Tuesday 09 February 2010 at 4:53 pm
Versão para impressão
Notas de aula são propriedade intelectual. Sendo assim, qualquer uso, no todo ou em parte, deve ter a origem referenciada apropriadamente, após autorização de seu autor.
O texto a seguir corresponde à anotações parciais de aula. Não é um texto em forma final, completo e totalmente revisado. Nesse caso, esse texto não tem como objetivo substituir livros sobre o assunto. Assim, esse texto deve ser entendido apenas como um guia de estudo para o aluno acompanhar a disciplina.
A seguir vamos calcular a trajetória percorrida por partículas α segundo o modelo de Rutherford. Um esquema da trajetória de uma partícula pode ser visto na figura abaixo.
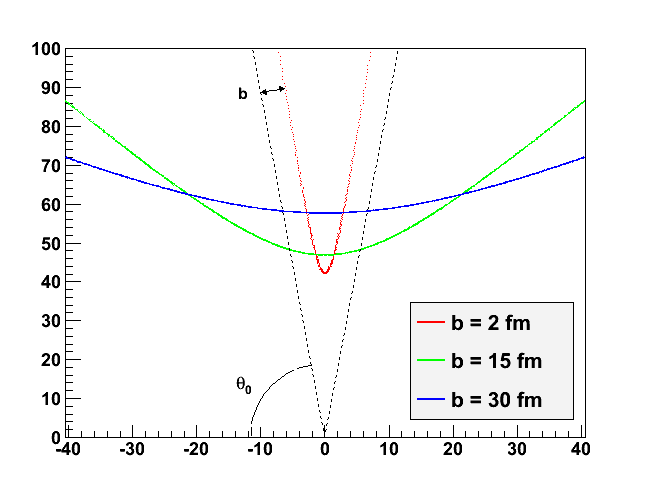
Figura 1 - Trajetória de partículas α em vários parâmetros de impacto sendo espalhadas por um núcleo de número atômico Z.
A Lagrangeana para para o sistema acima pode ser obtida através de:
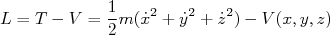 (1)
(1)
Para um sistema no qual o potencial é central, o problema pode ser tratado como planar e podemos escrever a Lagrangeana em coordenadas polares, ou seja:
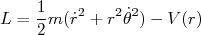 (2)
(2)
No caso do modelo de Rutherford, podemos escrever que a energia potencial vale:
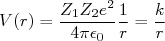 (3)
(3)
A partir da equação de Lagrange para forças conservativas:
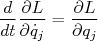 (4)
(4)
Com 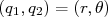 , podemos escrever que:
, podemos escrever que:
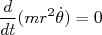 (5)
(5)
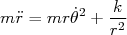 (6)
(6)
Da equação (5), podemos dizer que a quantidade 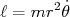 é conservada durante o movimento. Essa quantidade é o momento associado à variável θ e corresponde ao momento angular do sistema. Substituindo
é conservada durante o movimento. Essa quantidade é o momento associado à variável θ e corresponde ao momento angular do sistema. Substituindo 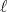 na equação (6), temos que:
na equação (6), temos que:
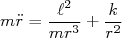 (7)
(7)
A equação acima pode ser resolvida após alguma manipulação algébrica. Primeiramente multiplicamos a equação acima por  e usamos as seguintes relações:
e usamos as seguintes relações:
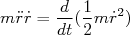 (8)
(8)
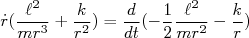 (9)
(9)
Substituindo as expressões (8) e (9) em (7), chega-se a:
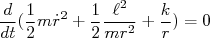 (10)
(10)
ou seja, a quantidade que está sendo derivada acima é uma constante do movimento. Essa quantidade é a energia total do sistema, ou seja:
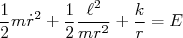 (11)
(11)
Há várias técnicas para resolver a equação (11) e obter a dependência temporal de r. Contudo, em experimentos realizados em física nuclear, não se mede trajetórias durante a interação. Mede-se valores assintóticos dessas trajetórias, como ângulos de espalhamento. Isso é devido ao fato dos detectores estarem posicionados à distâncias extremamente maiores que aquelas tipicamente envolvidas na interação entre as duas partículas (lembre-se que o núcleo possui dimensões da ordem de 10-15 m). Nesse caso, ao invés da dependência temporal de r é mais vantagem tentar obter uma expressão que relacione o ângulo de espalhamento com r, pois podemos tomar o seu valor assintótico no qual r é muito grande. Para fazer isso, devemos transformar a equação diferencial no tempo em uma equação diferencial de r em θ. Isso pode ser feito aplicando a regra da cadeia abaixo:
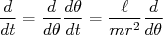 (12)
(12)
Também fazemos a mudança de variável 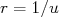 , de modo que:
, de modo que:
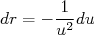 (13)
(13)
Substituindo (12) e (13) em (11), após alguma manipulação, temos:
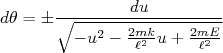 (14)
(14)
Integrando ambos os lados da equação (consulte uma boa tabela de integrais, a integral em du possui solução analítica) e desprezando as constantes que aparecem quando fazemos uma integral (isso não é importante, pois estaremos interessados em calcular o ângulo de espalhamento que é a diferença entre o ângulo incidente e o ângulo de saída assintóticos), temos:
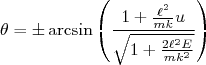 (14)
(14)
Essa expressão parametriza o movimento da partícula α pelo campo coulombiano devido ao núcleo atômico, como mostrada na figura no alto da página. Os sinais representam quadrantes diferentes da trajetória. Vamos tomar apenas a solução positiva. A condição assintótica do movimento ocorre quando o raio tende a infinito, ou seja, quando u tende a zero. Nesse caso, podemos simplificar a equação (14), além de inverter a expressão arcsin, de modo que:
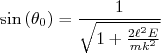 (15)
(15)
Que corresponde aos ângulos assintóticos do movimento, tanto antes como depois da interação. Como estamos interessados no desvio sofrido pela partícula em relação à sua direção inicial, é fácil ver que o desvio sofrido é 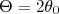 , ou seja:
, ou seja:
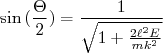 (16)
(16)
Usando a relação trigonométrica:
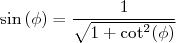 (17)
(17)
Escrevemos que:
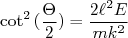 (18)
(18)
Como o momento angular é uma grandeza conservada durante o movimento, podemos calculá-lo assintoticamente, utilizando o parâmetro de impacto. Nesse caso, o momento angular vale, para uma partícula de velocidade v e parâmetro de impacto b:
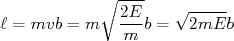 (19)
(19)
Assim:
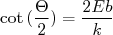 (20)
(20)
A expressão (20) é particularmente importante pois permite o cálculo da seção de choque de espalhamento da interação entre a partícula α e o núcleo estudado. Na figura abaixo mostramos trajetórias de várias partículas α em diferentes parâmetros de impacto. Note que quanto menor o parâmetro de impacto, maior o ângulo de espalhamento Θ da partícula incidente.
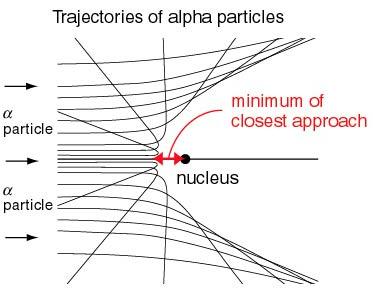
Figura 2 - Trajetórias de partículas α em diferentes parâmetros de impacto
Exercícios
- Mostre que no caso de uma força central podemos reduzir o movimento a um plano e escrever a lagrangeana desse sistema de acordo com (2).
- Para resolver o problema do espalhamento Rutherford não consideramos que o núcleo alvo pudesse recuar devido à interação com a partícula α. Porque? Obtenha o ângulo de espalhamento em função do parâmetro de impacto considerando o recuo do núcleo alvo.
- Calcule a distância de máxima aproximação da partícula α com o núcleo em função da sua energia e parâmetro de impacto da interação. Em uma colisão de parâmetro de impacto muito pequeno, qual seria a energia necessária para uma partícula α chegar a pelo menos 10 fm de distância de um núcleo de ouro.
Leitura recomendada
- Introductory Nuclear Physics, K. S. Krane, seção 11.6
Estava calculando a distância de maior aproximação da questão 3 e cheguei em algo que me pareceu estranho: quando o parâmetro de impacto for zero, a partícula incidente sempre vai chegar no núcleo (r=0), independente da energia. Está certo?!
Oi Caio
Não está certo. O problema para parâmetro de impacto pequeno é que o movimento é unidimensional e ai você tem que a equação de movimento em duas dimensões fica estranha. Isso porque l = 0 e r pode assumir qualquer valor, independente de θ. Nesse caso, é melhor pensar em um problema unidimensional. Por outro lado, qual expressão você obteve para a distância de máxima aproximação em função de b? Pode ser que dê para fazer uma conta de limite, nesse caso, dependendo de como você tocou o problema.


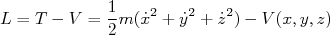 (1)
(1)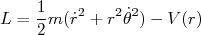 (2)
(2)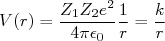 (3)
(3)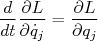 (4)
(4)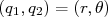 , podemos escrever que:
, podemos escrever que:
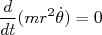 (5)
(5)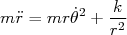 (6)
(6)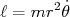 é conservada durante o movimento. Essa quantidade é o momento associado à variável θ e corresponde ao momento angular do sistema. Substituindo
é conservada durante o movimento. Essa quantidade é o momento associado à variável θ e corresponde ao momento angular do sistema. Substituindo 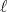 na equação (6), temos que:
na equação (6), temos que:
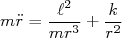 (7)
(7) e usamos as seguintes relações:
e usamos as seguintes relações:
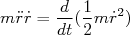 (8)
(8)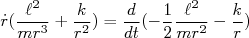 (9)
(9)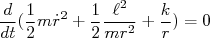 (10)
(10)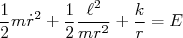 (11)
(11)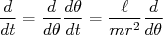 (12)
(12)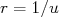 , de modo que:
, de modo que:
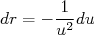 (13)
(13)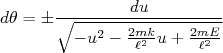 (14)
(14)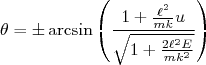 (14)
(14)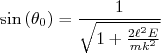 (15)
(15)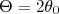 , ou seja:
, ou seja:
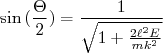 (16)
(16)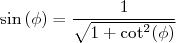 (17)
(17)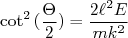 (18)
(18)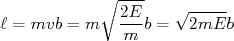 (19)
(19)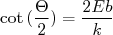 (20)
(20)