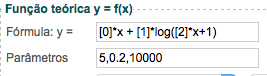Fórmulas, expressões matemáticas e ajustes de funções
From GRIPER Wiki
Contents |
Expressões matemáticas
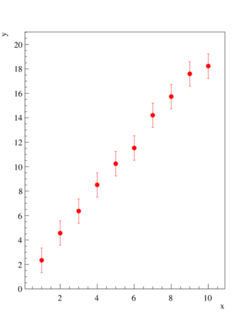
Em muitas situações de análise de dados, ou cálculos em geral, queremos aplicar expressões matemáticas a variáveis previamente definidas. Um exemplo bastante comum é o de ajuste de funções. Imagine um conjunto de dados como o mostrado na figura ao lado onde deseja-se ajustar uma expressão do tipo
y = ax + b
onde a e b são parâmetros que serão ajustados aos dados ao lado.
Acontece que nem sempre é possível escrever uma fórmula matemática desta maneira em um programa de computador. Cada programa possui uma sintaxe própria que deve ser respeitada. Isto não seria diferente no nosso caso. O WebROOT faz interface com o ROOT e, a menos de situações bem específicas que discutiremos adiante, a sintaxe utilizada no WebROOT para expressões matemáticas é a mesma utilizada pelo ROOT.
Assim, fórmulas e expressões matemáticas são escritas utilizando o padrão de linguágem do c++ e ROOT. A seguir apresentamos um breve tutorial.
Variável independente
No WebROOT, a variável independente em uma expressão é sempre x, se a expressão tiver apenas uma variável independente. Se tiver duas variáveis independentes, elas são x e y. Se houver três, x, y e z. Estas variáveis são escritas sempre com letra minúscula. Fique atento a isto.
Operadores matemáticos
Em c++, os operadores matemáticos básicos são o (+) para adição, (-) para a subtração, (*) para multiplicação, (/) para divisão e (%) para o resto de uma divisão. Não existe operador para potência em c++. Normalmente utiliza-se a função pow(a,b) = ab. Contudo, o ROOT também aceita o operador (^) para este fim. Assim, a^b = ab. No WebROOT, ambos formatos para potência são aceitos.
Funções matemáticas básicas
Há várias funções matemáticas pré-definidas no c++ (e ROOT), tais como sin(x), cos(x), tan(x), asin(x) (arco-seno), acos(x), atan(x) (x em radianos), exp(x), ln(x) (log na base e), log10(x) (log na base 10), pow(a,b), sqrt(x) (raiz quadrada), etc. Consulte a web para uma boa referência de funções pré-definidas em c++. Apesar disto, acredito que estas cobrem 99.9% do dia-a-dia do WebROOT.
Parâmetros em expressões matemáticas
Na expressão y = ax + b, a e b são parâmetros. No WebROOT, parâmetros são escritos como um número entre colchetes, por exemplo [0], [1], [2],... Assim, para escrever a equação de uma reta y = ax + b, no WebROOT, devemos escrever y = [0] * x + [1]. Note o * para representar a operação de multiplicação. Por comparação a = [0] e b = [1]. Na figura ao lado temos uma outra expressão matemática, y = ax + blog(cx + 1), que deve ser escrita como [0] * x + [1] * log([2] * x + 1). Note, nesta figura, que atribuímos valores aos parâmetros, separados por vírgulas. Assim a = [0] = 5, b = [1] = 0.2 e c = [2] = 10000.
Funções matemáticas extras do ROOT
| Exemplos de expressões matemáticas | |
|---|---|
| Expressão | WebROOT |
| ax + b | [0] * x + [1] |
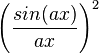
| ![(sin([0]*x)/([0]*x))\wedge 2](/wiki/images/math/5/4/f/54f350cf52b7cc58b897cd96d3e997fe.png)
|
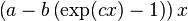
| ([0] − [1] * (exp([2] * x) − 1)) * x |
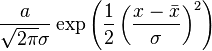
| gaus(0) |
Há várias funções matemáticas extras no ROOT que podemos utilizar. Veja o manual do ROOT para detalhes. Para citar as mais comuns:
- gaus(0) - Função gaussiana. [0] = amplitude, [1] = valor médio, [2] = desvio padrão
- gaus(3) - Função gaussiana. [3] = amplitude, [4] = valor médio, [5] = desvio padrão.
- polN(0) - Polinômio de grau N. Por exemplo, pol1(0), pol2(0), etc. Neste caso, polN(0) = [0] + [1]*x + [2]*x^2 + ... Temos pré-definido desde pol0 até pol9.
OBS: O valor (0) entre parêntesis, indica a numeraço inicial dos parâmetros. Por exemplo, gaus(3) indica que [3] = amplitude, [4] = valor médio e [5] = desvio padrão. Isto é útil quando escrevemos fórmulas complexas que envolvem várias funções pré-definidas.
Ajustes de funções
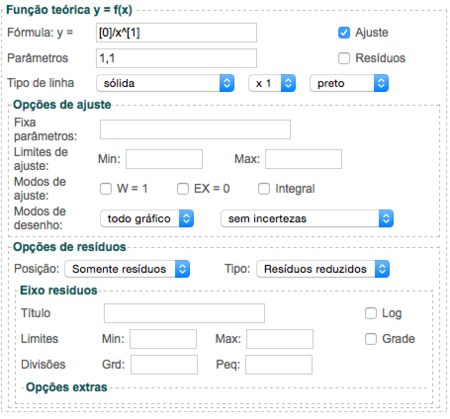
Muitas aplicações no WebROOT têm a possibilidade de realizar ajustes de uma função a um conjunto de dados. O ambiente de ajuste de funções segue o mesmo princípio em todas estas aplicações. A seguir discutiremos como isto é feito.
O WebROOT utiliza como padrão o Minuit para ajuste de funções. O método padrão utilizado é o MMQ (Método dos Mínimos Quadrados) onde o conjunto de parâmetros que ajustam uma função aos dados é obtido através da minimização do Chi2 entre os dados e a função. No caso de ajuste de funções aos dados em um gráfico, temos a opção de obter os resíduos do ajuste. Esta opção não está presente para ajustes de histogramas.
A figura ao lado mostra a interface de ajuste de funções, com todas as suas caixas internas expandidas.